Physics I: 1-5 Flashcards
base units
standard units around which the system itself is designed
derived units
created by associating base units with each other
vectors
numbers that have magnitude and direction
ex: displacement, velocity, acceleration, force
vector
examples
displacement, velocity, acceleration, force
scalars
numbers that have magnitude only
no direction
ex: distance, speed, energy, pressure, mass
scalar
examples
distance, speed, energy, pressure, mass
common notation for vector quantities
arrow or boldface
common notation for scalar quantities
italic
resultant
sum or difference of 2 or more vectors
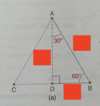
tip to tail method of vector addition
vector addition may be accomplished two ways:
- tip to tail method
- breaking a vector into its components and using the Pythagorean theorem
COMMUTATIVE
trig
X =
X = V cos theta
trig
Y =
Y = V sin theta
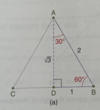
using Pythagorean theorem for vector addition
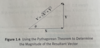
vector subtraction may be accomplished by
changing the direction of the subtracted vector and then following the procedures for vector addition
A - B = A + (-B)
NOT COMMUTATIVE
finding the resultant (R) of V1 + V2 + V3
- resolve the vectors to be added into their x and y components
- add the x components to get the Rx; add the y components to get Ry
- find the magnitude of the resultant by using the Pythagorean theorem
- find the direction (theta) of the resultant using tan-1
multiplying vectors by scalars
if a vector A is multiplied by the scalar value n, a new vector B is creased such that:
B = nA
mutiplying a vector by a scalar changes the _____ and may reverse the _____
magnitude
direction
multiply vectors by other vectors to get a scalar quantity
dot product
A • B = |A| |B| cos theta
dot product
multiplying 2 vectors to get a scalar quantity
A • B = |A| |B| cos theta
multiply vectors by other vectors to get a vector quantity
cross product
A x B = |A| |B| sin theta
use right hand rule
NOT commutative - order matters
cross product
multiplying 2 vectors to get a vector quantity
A x B = |A| |B| sin theta
steps to apply right hand rule
C = A x B
- point thumb in direction of vector A
- extend fingers in direction of vector B
- the direction your palm points is the direction of the resultant C
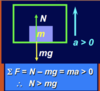
when calculating the sum of vectors A and B (A+B), we put the tail of B at the tip of A. what would the effect of reversing this order (B+A)?
vector addtn is a commutative function
the resultant of A+B is the same as B+A
when calculating the difference between vectors A and B (A-B), we invert B and put the tail of this new vector at the tip of A. what would the effect of reversing this order (B-A)?
vector subtraction is not a commutative function
the resultant of A-B has the same magnitude as B-A but is oriented in the opposite direction
how is a scalar calculated from the product of two vectors?
dot product
A • B = |A| |B| cos theta
how is a vector calculated from the product of two vectors?
cross product
A x B = |A| |B| sin theta
displacement
x
net change in position
vector
distance
d
path traveled
scalar
velocity
v; unit: m/s
change in displacement with respect to time
vector
speed
actual distance traveled in a given unit of time
scalar
average velocity
total displacement divided by total time
vector
average speed
total distance traveled divided by the total time
scalar
instantaneous velocity
limit of the change in displacement over time as the change in time approaches zero
vector
instantaneous speed
magnitude of the instantaneous velocity vector
scalar
what is the relationship between instantaneous velocity and instantaneous speed?
instantaneous speed is the magnitude of the instantaneous velocity vector
what is the relationship between average velocity and average speed?
average speed and average velocity may be unrelated because speed does not depend on displacement, but is rather the total distance traveled divided by time
t/f
total distance traveled can never be less than the total displacement
true
when to covert to scientific notation
most of the time
especially when answers differ by powers of 10
exception: square roots
when rounding numbers to be multiplied…
round one number up and one number down
when rounding numbers to be divided…
round both numbers in the same direction
X0 =
1
XA x XB =
X(A+B)
XA / XB =
X(A-B)
(XA)B =
X(AxB)
(X/Y)A
XA / YA
X-A =
1 / XA
two ways to estimate square roots of numbers less than 400:
- approximate by determining the perfect squares it can break down into
- divide the number by known squares to reduce it
sqrt of 2
1.414
sqrt of 3
1.732
logA1 =
0
logAA =
1
log A x B =
log A + log B
log (A/B)
log A - log B
log AB =
B log A
log (1/A) =
- log A
convrt log to ln
log x = ln x / 2.303
log (n x 10m) =
m + log(n)
estimate sqrt 392
estimate log 7,426,135,420
two types of special right triangles
- 30-60-90
- 45-45-90
trig ratios
sin
sin 0 = √0 /2
sin 30 = √1 /2
sin 45 = √2 /2
sin 60 = √3 /2
sin 90 = √4 /2
trig ratios
cos
sin but reversed
cos 0 = √4 /2
prefix abbreviation: T
tera
1012
prefix abbreviation: G
giga
109
prefix abbreviation: M
mega
106
prefix abbreviation: k
kilo
103
prefix abbreviation: h
hecto
102
prefix abbreviation: d
deci
10-1
prefix abbreviation: c
centi
10-2
prefix abbreviation: m
milli
10-3
prefix abbreviation: μ
micro-
10-6
prefix abbreviation: n
nan-
10-9
prefix abbreviation: p
pico
10-12
convert C to K
K = C + 273
convert C to F
F = 9/5 C + 32
first law of thermodynamics
law of inertia
a body either at rest or in motion with constant velocity will remain that way unless a net force acts upon it
Fnet = ma
second law of thermodynamics
no acceleration will occur when the vector sum of the forces results in a cancellation of those forces
Fnet = ma
third law of thermodynamics
to every action, there is always an opposed by equal reaction
FAB = -FBA
linear motion
- motion in which the velocity and acceleration vectors are parallel or antiparallel
- includes free fall
What is the first of the Four Essential Kinematics Equations for the MCAT: Average Velocity (v̅) in terms of displacement (∆x)?
v̅ = ∆x/∆t
v̅ = Average Velocity (m/s) ∆x = Displacement (m) ∆t = Change in Time (s)
What is the second of the Four Essential Kinematics Equations for the MCAT: Average Acceleration (a̅) in terms of Change in Velocity (∆v)?
a̅ = ∆v/∆t
a̅ = Average Acceleration (m/s^2) ∆v = Change in Velocity (m/s) ∆t = Change in Time (s)
Essential Kinematics Equations: 3. What is the equation for displacement (x), in terms of Acceleration (a) and Initial Velocity (v0), without final velocity (v)?
x = v0t + (a · t^2)/2
x = Displacement (m) v0 = Initial Velocity (m/s) t = Time (s) a = Acceleration (m/s^2)
Essential Kinematics Equations: 4. What is the Equation for Final Velocity (v) in terms of acceleration (a), Initial Velocity (v0), and displacement (x), without Time (t)?
v^2 = v0^2 + 2ax
x = Displacement (m) v0 = Initial Velocity (m/s) v = Final Velocity (m/s) a = Acceleration (m/s^2)
acceleration due to gravity
g = 9.8 m/s2
projectile motion
- follows a path along 2 dimensions
- contains both an x and y component
- assuming negligible air resistance, the only force acting on the object is gravity
inclined planes
- 2D movement
- dimensions are parallel and perpendicular to the surface of the plane
uniform circular motion
only force is centripetal force, pointing radially inward
instantaneous velocity always points tangentially
free fall
max height
v =
0
circular motion
when forces cause an object to move in a circular pathway
centripetal force
Fc =
Fc = mv2 / r
how do the forces acting in free fall and projectile motion differ?
the only force acting in both free fall and projectile motion is gravity
at what angle of launch is a projectile going to have the greatest horizontal displacement?
- product of sin and cos is maximized when the angle is 45
- bc horizontal displacement relies on both measurements, the max horizontal displacement will also be achieved at this angle
at what angle of launch is a projectile going to have the greatest vertical displacement?
vertical displacement will always be zero as the object returns to the starting point
objects launched vertically will experience the greatest vertical distance
dynamics
study of force and torques
translational equilibrium
occurs in the absence of any net forces acting on an object
an object in translational equilibrium has a constant velocity, and may or may not be in rotational equilibrium
an object in translational equilibrium has…
a constant velocity, and may or may not be in rotational equilibrium
rotational equilibrium
occurs in the absence of any net torques acting on an object
rotational motion may consider any pivot point, but the center of mass is most common
an object in rotational equilibrium has a constant angular velocity
an object in rotational equilibrium has…
a constant angular velocity
Fg =
mg
fulcrum
fixed pivot point
log (n x 10^m) =
m + 0.n
If Max got in his car and traveled northwest, with a 63.2° angle between his direction and due west, how far west (in miles) would he have gone if he went 26.6 miles in the northwest direction?
(A) 4.6
(B) 12.0
(C) 16.8
(D) 34.2
(B) 12.0
cosθ = adjacent/hypotenuse cos63.2 = adjacent/26.6 adjacent = (26.6)(cos63.2) adjacent = (26.6)(approx. .5 (actual: .451)) adjacent = (approx. 13.3 (actual: .12.0))
Rusev started on an xy-plane at (-0.5, 3). He walks so that his final position is (-0.5, -3). What is Rusev’s displacement?
(A) -6 units
(B) 6 units
(C) -3 units
(D) 3 units
(A) -6 units
Displacement = Final Position - Initial Position = Net Distance (in some direction)
X-displacement = -0.5 - (-0.5) = 0
Y-displacement = (-3) - 3 = -6
Total displacement is 6 units due South.
If there is displacement in multiple directions (for example, in both the x and y directions), then the distance formula will be needed. Write out the distance formula for 2- and 3-dimensional movement
In which of the following examples could you calculate the missing variable from given information?
I. Given Distance and Initial Position, find Final Position.
II. Given Final Position and Distance, find Initial Position.
III. Given Initial Position and Final Position, Find Displacement.
(A) I only
(B) III only
(C) I and II only
(D) I, II and III
(B) III only
If you know the Initial and Final position, you can find Displacement. However, knowing distance cannot help to find Initial or Final Positions, since distance has no direction, only magnitude!
True or false? If an object’s velocity is zero, then the object’s acceleration must also be zero. If false, provide a counterexample.
False. Even if an object’s velocity is zero, the object could still be accelerating. Think of a baseball thrown straight up into the air; there is a split second where the ball is not moving up or down (at it peak height), but gravity is still making the ball accelerate back towards the Earth.
True or false? An object’s average acceleration must be in the same direction as the object’s net change in velocity. If false, provide a counterexample.
True. An object’s average acceleration must be in the same direction as the object’s net change in velocity.
What is the equation for Torque?
Torque = Force x Distance
(distance is from fulcrum or center of gravity)
Fill in the blanks: The _______________ is where the center of gravity of the object would be, and the ___________ is the distance from that center of gravity to where the force causing the torque is applied.
(A) Fulcrum, Torque Arm
(B) Fulcrum, Radius
(C) Lever Point, Torque Arm
(D) Lever Point, Radius
(A) Fulcrum, Torque Arm
The Fulcrum is where the center of gravity of the object would be, and the Torque Arm is the distance from that center of gravity to where the force causing the torque is applied.
Compare Translational and Rotational Equilibria.
Translational Equilibrium occurs if and only if the net forces acting on an object are equal to zero. Rotational Equilibrium occurs if and only if the sum of all torques acting on an object are equal to zero.
True or false? The further that the mass or force is from the axis of rotation, the easier it is to rotate.
True. The further that the mass or force is from the axis of rotation, the easier that it is to rotate.
To remember this, think of the equation for torque and having a longer lever arm.
Could an object be moving with a non-zero linear velocity and be in Dynamic Equilibrium? How about a non-zero angular velocity? Why or why not?
An object can be in Dynamic Equilibrium and still have a non-zero linear and/or angular velocity. The key is that there is no current net forces acting on the objects, so they must have no acceleration (be moving at a CONSTANT linear or angular velocity).
If there is an object that is in Dynamic Equilibrium, which of Newton’s Laws will best dictate how the object will move?
(A) Newton’s First Law
(B) Newton’s Second Law
(C) Newton’s Third Law
(D) I will go study Newton’s Laws again then come back to answer this!
(A) Newton’s First Law
Newton’s Law of Inertia states that an object in motion will stay in motion or that an object at rest will stay at rest until the object is no longer in Dynamic Equilibrium.
Compare Static and Dynamic Equilibrium.
Dynamic Equilibrium allows for a constant velocity, only requiring that Translational and Rotational Equilibria are maintained. For Static Equilibrium, not only must Translational and Rotational Equilibria be maintained, but also the object’s velocity must be equal to 0.
Johnny gets on the elevator. He has a mass of 103.54 kg (too many sweets, Johnny). The elevator starts accelerating upwards at 2.13 m/s^2. What is the Normal force acting on Johnny (in N)?
(A) 786.34
(B) 942.01
(C) 1235.23
(D) 1654.90
(C) 1235.23
Force of Gravity = 103.54 x -9.8 = -980 N (-1014.69)
Net Force = 103.54 kg x 2.13 m/s^2 = 200 N (actual: 220.54)
Force of Gravity + Normal force = Net Force
-1014.69 N + Normal Force = 220.54 N
Normal Force = 1180 N (actual: 1235.23)
Johnny is hanging onto two wires. One of them connects to the ceiling forming a 30 degree angle with the ceiling. The other is connected to a wall and is parallel to the ceiling (see backside of notecard for a visual representation). Johnny weighs 750 N (he has been on a diet). What is the tension in the horizontal wire (in N)?
(A) 320
(B) 651
(C) 874
(D) 1299
(D) 1299
Angle = 30 degrees
Force downward = 750 N
y axis tension in wire 1 = 750N
tension in wire 1 = 750/sin(30) = 1500N
tension in wire 2 = x axis tension in wire 1 = 1500cos(30) = 1299N
Draw a diagram showing all the forces acting on a box on an inclined plane. Break the force of gravity up into the components that are parallel and perpendicular to the surface, and define the size of these forces relative to the force of gravity, and the angle of the incline.
When drawing a Free Body diagram for a box on an inclined plane, which of the angles relating to the box and the plane will be equal to the angle the inclined plane makes with the flat ground? Draw it out.
Where the two thetas are written, the angles are equal!
d
b
a
c
c
a
Which of the following statements about Terminal Velocity are true?
I. Terminal Velocity can differ for the same free-falling object, depending on the medium it falls through.
II. Terminal Velocity is characterized by oscillating accelerations, leading to a constant velocity.
III. Terminal Velocity is only possible on Earth.
(A) I only
(B) II only
(C) I and II only
(D) I, II and III
(A) I only
Each of the following statements about terminal velocity are true:
I. Terminal Velocity can differ for the same free-falling object, depending on the medium it falls through.
II. Terminal Velocity is characterized by the forces of gravity and resistance through the medium being traveled through being equal and opposite, leading to a constant velocity.
What is the equation for final velocity in terms of initial velocity and acceleration?
(Final Velocity) = (Initial Velocity) + ((Time)x(Acceleration))
True or false? Inertia dictates the velocity of an object if the acceleration of that object is zero.
True. Inertia dictates the velocity of an object if the acceleration of that object is zero.
True or False? Speed will always be changed by an unbalanced force acting on the object.
False. An unbalanced force can change the direction of an object without changing the speed. The sentence should say, “VELOCITY will always be changed by an unbalanced force acting on the object.”
True or false? The baseball still traveling in a direction opposing the net force acting upon the baseball can be attributed to inertia.
False. Inertia would apply if there had been no net force acting on the baseball at all. There clearly is a force exerted on the baseball by the window, as stated in the question stem.
In order to solve problems involving acceleration, velocity, and displacement, you need to know the four Linear Motion (Kinematics) equations. Write them out.
True or False? The Center of Mass is located at the very center of an object that has a mass.
False. The Center of Mass is located at the mean position of mass in a body or system. It is where gravity can be assumed to act on the object.
What will happen if a force acts on an object, but not on its center of mass?
The object will rotate around the center of mass.
b
a
d
a
c (b.)
a
d
c
force
F
vector
experienced as pushing or pulling on objects
SI: newton (N)
gravity
attractive frce that is felt by all forms of matter
magnitude of gravitational force between 2 objects is
Fg =
(G m1 m2) / r2
G = universal gravitational constant
acceleration due to gravity, g, __inc/dec__ with height above the earth and __inc/dec__ the closer one gets to the earth’s center of mass
dec
inc
friction
force that opposes the movement of objects -> causing it to slow down or become stationary
static friction
fs
exists between stationary object and surface its on
coefficient of static friction
μs
dependent on the two materials in contact
static friction eq
normal force
component of the force between two objects in contact that is perpendicular to the plane of contact between the object and surface upon which it rests
kinetic friction
fk
exists between a sliding object and the surface over which the object slides
kinetic friction eq
fk = μkN
which one is always larger: μs or μk? why?
μs is always larger
objects will stick until they start moving, and then will slide more easily over one another
weight
Fg
measure of gravitational force
vector
mass
m
measure of a body’s inertia
independent of gravity
scalar
eq that relates weight and mass
Fg = mg
acceleration
a
rate of change of velocity that an object experiences as result of some applied force
vector
velocity vs time graph
instantaneous acceleration
tangent to the graph at any time t that corresponds to the slope of the graph at that time
when calculating frictional forces, how is directionality assigned?
direction of frictional force always opposes movement
energy
system’s ability to do work or make something happen
kinetic energy
K
energy of motion
SI: joule (J)
kinetic energy eq
K = 1/2 mv2
v = speed
the faster objects, the __more/less__ kinetic energy they have
more
what in kinetic energy dependent on? why?
speed (not velocity)
an object has the same kinetic energy regardless of the direction of its velocity vector
potential energy
U
energy that is associated with a given object’s position in space or other intrinsic qualities of the system
gravitational potential energy
depends on object’s position with respect to some level
gravitational potential energy eq
U = mgh
elastic potential energy
related to the spring constant and the degree of stretch or compression of a spring
elastic potential energy eq
U = 1/2 kx2
k = spring constant
spring constant
k
measure of the stiffness of a spring
total mechanical energy
E
sum of an object’s potential and kinetic energy
total mechanical energy eq
E = U + K
conservation of mechanical energy
first law
energy is never created nor destroyed - its is merely transferred from one form to another
conservative forces
+ 2 exs
path indepedent
do not dissipate energy
ex: gravitation and electrostatic energy
two methods of determining if a force is conservative:
- when object comes back to its starting position
- if net change in energy = 0 –> conservative
- when object undergoes a particular displacement
- if net change in energy is the same regardless of path –> conservative
conservation of mechanical energy eq
ΔE = ΔU + ΔK = 0
nonconservative forces
total mechanical energy is not conserved
path dependent
nonconservative forces exs
friction, air resistance, viscous drag
nonconservative forces eq
Wnonconservative = ΔE = ΔU + ΔK
for nonconservative forces, the longer the distance traveled, the ____ the amount of energy dissipated
larger
work
W
process by which energy is transferred from one system to another
the only way anything occurs (+ heat)
work eq
W = F • d = Fd cos theta
d = magnitude of displacement
theta = angle between applied force vector and displacement vector
when a gas expands, work was done ____
work is __pos/neg__
by the gas
positive
when a gas is compressed, work was done ____
work is __pos/neg__
on the gas
negative
isovolumetric or isochoric process
volume is constant
isobaric process
pressure is constant
work eq for isobaric processes
W = PΔV
P = pressure
V = volume
power
P
rate at which energy is transferred from one system to another
SI: watt (W)
power eq
P = W / t = ΔE / t
work energy theorem
net work done by forces acting on an object will result in an equal change in the object’s kinetic energy
work energy theorem eq
Wnet = ΔK = Kf - Ki
what are the units for work?
joule J
how are work and energy different?
by performing work, the energy of a system is changed.
work is a form of energy transfer
provide 3 methods (eqs) for calculating the work done by or on a system
- W = Fd cos theta
- W = PΔV
- Wnet = ΔK
simple machines
designed to provide mechanical advantage
mechanical advantage
ratio of magnitudes of the force exerted on an object by a simple machine (Fout) to the force actually applied on the simple machine (Fin)
mechanical adnvantage eq
= Fout / Fin
Fout = force exerted on an object by simple machine
Fin = force applied on simple machine
pulleys
a reduction of necessary force at the cost of increased distance to achieve a given value of work or energy transference
allow heavy objects to be lifted using a much reduced force
efficiency
ratio of the machine’s work output to work input when neoconservative forces are taken into account
efficiency eq
= Wout / Win = (load * load distance) / (effort * effort distance)
as the length of an inclined plane increases, what to the force required to move an object the same displacement?
as the length of an inclined plane increases, the amount of force necessary to perform the same amount of work (moving the object the same displacement) decreases
as the effort decreases in a pulley system, what happens to the effort distance to maintain the same work output?
as the effort (requires force), decreases in a pulley system, the effort distance increases to generate the same amount of work
what accounts for the difference work input and work output in a system that operates at less than 100% efficiency?
the decrease in work output is due to nonconservative or external forces that generate or dissipate energy
Which of the following about the equations for Friction are correct?
I. The equations for Friction are Vector Equations.
II. To determine the direction of the Friction Vector, you must use the Right Hand Rule.
III. The Friction Equations will give you the magnitude of the Friction, but not direction.
(A) I only
(B) II only
(C) III only
(D) I and II only
(C) III only
The Friction Equations are NOT Vector Equations, so they will only give a magnitude of Friction. The direction of Friction will be opposing the direction of motion.
True or false: Even though the calculation of static friction [(coefficient of static friction)·(normal force)]could exceed the other forces acting on an object, static friction will not cause an object to accelerate.
True. Even though the calculation of static friction [(coefficient of static friction)·(normal force)] could exceed the other forces acting on an object, static friction will not cause an object to accelerate.
Remember, this is STATIC friction. At its strongest, it only keeps position the same, not cause acceleration!
A block is sitting on a flat surface, with a weight of 100 N. If it takes a force of 73 N to just barely start moving the block, what is the coefficient of static friction (μs)?
(A) .54
(B) .62
(C) .73
(D) .81
(C) .73
Fs ≤ μs·Fn
73 = μs x 100
μs = 73 N/100 N
μs = 0.73
True or false? Unlike Static Friction, which could vary with the amount of force being applied, Kinetic Friction is a constant value for any given coefficient of friction and normal force, meaning that it can cause deceleration.
True. Unlike Static Friction, which could vary with the amount of force being applied, Kinetic Friction is a constant value for any given coefficient of friction and normal force, meaning that it can cause deceleration.
What is the relationship between the coefficient of static friction and the coefficient of kinetic friction?
coefficient of kinetic friction ≤ coefficient of static friction
Another example where the Normal Force is not necessarily equal to Gravity is when there is a vertical net force. For example, when riding in an elevator down 10 floors, the elevator slows down before stopping. While the elevator is slowing its descent, would the Normal Force be greater than or less than the force of Gravity?
(Hint: Draw a Free Body Diagram!)
Because the elevator is accelerating upwards, the Net Force must be going up. This means that the Normal Force must be greater than the force of Gravity!
d
c
d
d
b
d
a
b
c
True or false? If there is an obtuse angle between Force and Displacement, then the Work done by the force must be negative.
True. If there is an obtuse angle between Force and Displacement, then the Work done by the force must be negative.
This is because the cosine of the angle is negative!
If a 9.76 kg ball is raised to a height of 10.34 m, what is the potential energy of the ball (in J)?
(A) 675.8
(B) 865.3
(C) 989.0
(D) 1143.6
(C) 989.0
PE = mgh PE = (9.76)(9.8)(10.34) PE = approx. 1000 (989.00)
True or false? All changes in potential energy are equal to the opposite of work done by gravity (PE = -Wgrav).
False. Changes in potential energy due to gravity are equal to the opposite of work done by gravity (PEgrav = -Wgrav).
What is the equation for Hooke’s law (restorative force of a spring in terms of displacement)?
F = -kx
F = Restorative force k = spring constant x = displacement
If a box has a mass of 5.34 kg, and is pushed by a spring for 4.89 m, giving it a velocity of 11.29 m/s, what is the spring constant for that spring (in N/m)?
(A) 14.5
(B) 21.5
(C) 28.5
(D) 43.5
C) 28.47
KE = 1/2 mv^2 KE = (.5)(5.34)(11.29)^2 KE = approx. 350 J (actual: 340)
KE = PE = 1/2 kx^2
340 J = k(.5)(4.89)^2
k = approx. 30 kg/s^2 (actual: 28.5)
Note: kg/s^2 is equivalent to N/m
Is Gravitational Force a conservative or non-conservative force? Friction? Force of a Spring? Air Resistance?
Conservative: Gravitational force, Force of a Spring
Non-conservative: Friction, Air Resistance
How much power does it take to lift a 96.57 kg weight 1.34 m into the air in 7.25 seconds?
(A) 97.65
(B) 174.92
(C) 302.65
(D) 425.43
(B) 174.92
Work Done = PE = mgh
PE = (96.57)(9.8)(1.34) = approx. 1000 J (actual: 1268.16)
Power = work/time Power = 1268.16 J / 7.25 s Power = approx. 200 J/s (actual: 174.92)
What is the equation for instantaneous power in terms of velocity?
Power = Force x Velocity
If a car is moving 28.76 m/s and the engine is applying a force of 114.89 N, what is the power output of the engine at that moment (in W)?
(A) 2164.32
(B) 2597.65
(C) 3304.24
(D) 4587.92
(C) 3304.24
Power = Force x Velocity Power = (114.89)(28.76) Power = approx. 3000 J/s (actual: 3304.24)
In which of the following scenarios would you be able to calculate the appropriate variable?
I. Given Gravitational Potential Energy and Elastic Potential Energy, find Kinetic Energy.
II. Given Kinetic Energy and Mechanical Energy, find Elastic potential Energy.
III. Given total Potential Energy and Mechanical Energy, find Kinetic Energy.
(A) I only
(B) III only
(C) I and II only
(D) I and III only
(B) III only
In the following scenario, you would be able to find the asked-for variable:
Given total Potential Energy and Mechanical Energy, find Kinetic Energy.
I. You have no Mechanical Energy.
II. You have no way to differentiate between Elastic and other forms of Potential Energy
What is the Conservation of Total Mechanical Energy Equation in its general form? How would you write it out using Kinetic and Potential Energy?
In its general form:
Einitial = Efinal
See image for other form.
True or False? Conservation of Total Mechanical Energy claims that any forces acting on objects will not affect the total Mechanical Energy of the system.
False. Conservation of Total Mechanical Energy claims that any Conservative Forces acting on objects will not affect the total Mechanical Energy of the system.
If the Non-Conservative Force of Friction is acting on an object, then how would you write out the Conservation of Mechanical Energy Equation?
Note: Any Non-Conservative force could be in the place of friction here.
If a 18.77 N box is sitting on one end of a lever at a distance of 1.32 m from the fulcrum, how much force must be applied to at a distance of 4.35 m from the fulcrum to raise the box?
(A) 3.43
(B) 4.89
(C) 5.70
(D) 7.42
(C) 5.70
f1 x d1 = f2 x d2
18.77 x 1.32 = 4.35 x f2
f2 = approx. 6 N (actual: 5.70)
What is the difference between work and moment when dealing with mechanical advantage?
Both work and moment are equal to distance times force, but with work the force is in the same direction as the distance, with moment the distance is perpendicular.
Unrelated to Moment, what is the equation for Momentum?
p = mv
p = Momentum m = Mass v = Velocity
b
a
c
c
d
c
a
d
d
b
d
a
c
b
c
d
c
a
a
