Non-Linear Data Structures Flashcards
1
Q
What is Big O notation?
A
Big O is a mathematical notation
Time/space complexity
that describes the limiting behavior of a function where the argument tends toward a particular value or infinity.
2
Q
When do we use Big O notation?
A
To determine the scale-ability of an algorithm as input grows large.
3
Q
What does Big O describe?
A
The performance on an algorithm
4
Q
What does Big O have to do with data structures?
A
Certain operations can be more or less costly depending on what data structure is used (Array, Linked List, Queue, etc)
5
Q
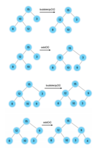
Name the different time complexities.
A
6
Q
What is exponential time complexity?
A
The opposite of logarithmic time complexity.
The exponential curve grows faster as the input grows.
7
Q
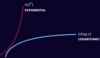
Which is time complexity more efficient?
log(n)
O(n)
A
While O(n) grows linearly with greater input,
O(log n) slows down at some point.
This makes O(log n) quadratic time more efficient that O(n) linear time.
8
Q
At what point does the logarithmic algorithm slow down?
A
at some point, O(log n) will slow down.
When we reduce our work in half every step.
9
Q
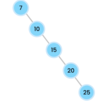
What is the Big-O for linear search vs. binary search?
A
linear search = O(n).
Iterate an array.
binary search = O(log n).
search a binary tree.
10
Q
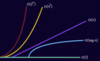
What are the five most common time complexity curves?
A
11
Q
What are non-linear data structures?
A
- Binary Trees
- AVL Trees
- Heaps
- Tries
- Graphs
12
Q
When would we have a quadratic Big-O value?
A
When we use nested loops that each performs an iteration over the entire set of values.
13
Q
What is logarithmic time complexity?
A
When we throw out half our items and narrow our search.
o(log n) - binary search tree lookup
14
Q
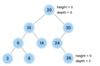
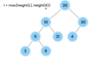
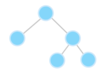
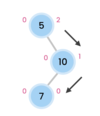
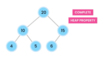
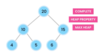
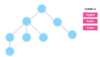
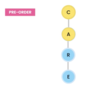
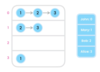
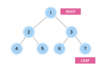
What is a tree?
A
A nonlinear data structure
stores elements in a hierarchy.
The “elements” are referred to as “nodes.”
Each “node” has data or values (could store objects).
The “lines” that connect “nodes” are called “edges.”
15
Q
What are real-world applications of trees?
A
Tons of applications
databases
graphical user interfaces
websites
- Hierarchical data (files, folders) - File systems on your computer
- Databases (indexing) - use trees for indexing for fast database lookup.
- Autocompletion (matching previous queries) - Storing old search queries in a tree than trying to match old search queries to new entries.
- Compilers (translate code into new languages)
- Compression algorithms (JEPG, MP3)
16
Q
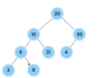
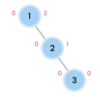
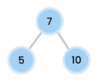
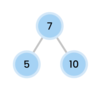
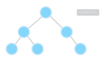
What is special about a binary tree?
A
Allows for logarithmic time complexity
left subtree is smaller than root
right subtree is greater than root
17
Q
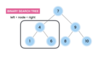
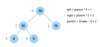
What is the top node of a tree called?
A
The top node is a tree is called “the root.”
The root node has two children in a binary tree.
18
Q
What are the children nodes called in a tree?
A
The children nodes of a root node are called “leaves.”
19
Q
What is the run time complexity of various operations on binary trees?
A
Logarithmic time complexity
Lookup ( ) : O(log n)
addItem ( ) : O (log n)
deleteItem ( ): O (log n)
**if a tree isn’t set up properly the performance may degrade to O(n).
20
Q
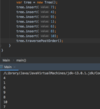
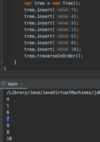
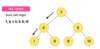
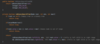
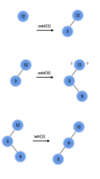
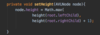
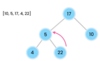
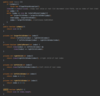
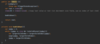
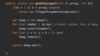
What values are we going to use for our binary search tree algorithm implementation?
A
21
Q
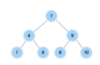
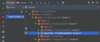
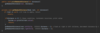
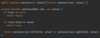
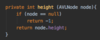
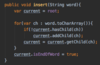
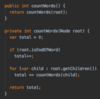
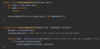
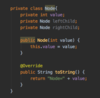
How do we implement the Node { } class in our binary tree?
A
22
Q
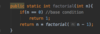
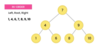
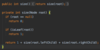
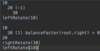
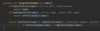
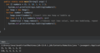
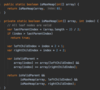
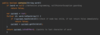
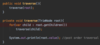
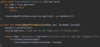
How do we implement the addItem( ) method in our binary search tree?
A
O ( log n ) operation!
23
Q
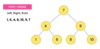
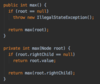
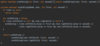
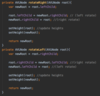
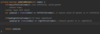
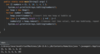
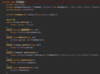
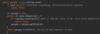
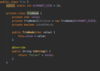
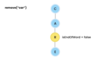
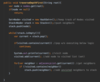
How do we implement the lookup( ) method in our binary tree?
A
O(log n) time complexity
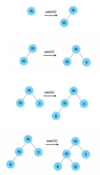
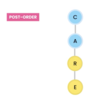
Traversal:
Root, leftChild, rightChild
24
Q
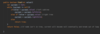
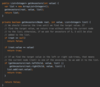
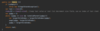
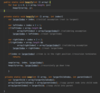
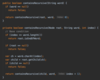
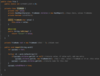
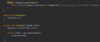
How do we implement a recursive method for printing nodes in traversePreOrder ( )?
A
Kick off recursion with method overloading
End with base condition
25
How do we implement a **recursive method** for printing nodes in **traversePostOrder ( )**?
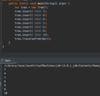
Kick off **recursion** with **method overloading**
End with **base condition**
26
How do we implement a recursive method for printing nodes in **traverseInOrder ( )**?
27
BT How do we implement **traverseLevelOrder ( )** in our binary **tree class**?
**O ( n ) operation**!
Have to **traverse every node** in the tree.
28
BT How do we implement **min ( )** in our **non-binary tree**?
**O(n) operation**!
Have to traverse all **values in tree**!
**Post order** traversal.
We start with the **leaves**.
We find the **min value** in the **left** and **right subtrees**.
compare **with root**
29
How do we implement **min ( )** in our **binary-search** tree?
**O(log n)** operation!
We are only trying to find the **left most leaf.**
In **every cycle**, we are **throwing out half of the nodes** in the tree.
30
How do we implement **equal ( )** method?
**Pre-order traversal**
**root,** **leftChild, rightChild**
**First**, compare the **root nodes** to check if **equal.**
**Then**, **use recursion** to look at their **children nodes** and **compare if equal.**
31
What are **two properties** of **tree nodes**?
**Depth** and **height**
**Depth = start at root**, move down
**Height =** **start at leaf**, move up
32
How do we **calculate depth (distance)** in our **tree**?
Counting **number of edges** from **root** to **node (target)**
**Height of root is zero**
**Ex. 8** has a depth of **3**
33
What is **recursion**?
**implementing repetition**
when a function calls the method itself
we have a cycle
**Terminating recursion**:
We will call this method forever!
need a base condition to terminate
**Java Implementation**:
Java **uses a stack** for **recursion** (**storing values**)
34
How is **recursion executed**?
During **each** **recursive method** call
**return value** is **stored in a stack**
**base condition is reached**
**result of last recursive method** is **returned to the previous method** calls
**This continues using the stack**
**until finally,** results of expressions will return from **first method call**
**\*\*Java** knows how to get **back to previous step** using a **stack**!
35
How do we **calculate height?**
**longest path** from **leaf** to **target node**
**Height** of **leaf node** is **zero**
**Ex. 20 (root) height is 3**
Formula (**height of tree**)**?**
1 + **max** ( **height(L)**, **height(R)** )
36
How do we implement the **height ( )** method in our binary tree?
37
What is **breadth-first** tree traversal?
aka **level order traversal**
visit all **nodes** in the **level** **before** visiting the **child nodes** below the level.
Traversing **level by level**.
38
What is **depth-first** traversal?
39
What is **pre-order** traversal?
**root, left subtree, right subtree**
Start at root, go deep to all children and grandchildren
**depth traversal!**
40
What is **in-order** **depth traversal**?
**depth first traversal**
start deep at **left leaf node, root, right node**
values come out in **ascending order**
reverse for **descending order**
rightChild, root, leftChild
41
What is **post-order traversal**?
depth **first traversal**
**leaves to root**
**start with left node, right node, branch root**
Used in **sorting data**, **heap properties,** and **mapping data connections**.
**Why?**
**start at the leaf nodes** to **calculate distances (height, depth)** before **moving to root nodes**.
42
What **powers non-linear traversal**?
**Recursion**
**calling a function again**
used for tree traversal algorithms like **HeapSort** and **BubbleUp.**
43
How does the binary search algorithm work?
It begins in the middle of the data set.
In every set, it narrows the search by half.
with a million data values, we can find our value in only 19 comparisons.
44
How do we implement a method **equal ( )** to validate if **two trees** are **equal?**
Popular **interview question!**
Write a method **equal ( )** to validate if **two trees** are **equal**
45
How can we implement **isBinarySearchTree ( ) ?**
**Popular Interview Question:**
Write code to **validate** this **binary tree**
(Is this tree a **binary search tree**?)
**Hint:**
**Pre-order traversal**
check if **each node** is in the **right range** (vs. comparing to other nodes)
46
How do we implement **getNodesAtDistance ( )** in our binary search tree?
**Popular Interview Questions:**
Write code to print all **nodes at distance k** from root.
**Hint:**
use recursion
Think of **breaking the problem down** into **smaller parts**.
Decriment the **distance** as we **traverse nodes**
eventually **distance reaches zero**, print nodes
47
Implement **size ( )** method to calculate the **size of a binary tree**.
48
Implement **max ( )** to **return the maximum value** in a binary tree **using recursio**n.
49
If our binary search tree is not structured properly what does our Big-O drop to?
O(n)
50
Implement **countLeaves ( )** to count **number of leaves** in a **binary tree**.
51
implement **contains ( )** to check for the **existence of a value** in a **binary tree using recursion**.
52
Implement **areSibling ( )** to check to see if **two values** are **siblings in a binary tree**.
53
Implement **getAncestors ( )** to return the **ancestors of a value** **in a List**
54
Implement **isBalanced ( )** method to check if a **binary tree is balanced.**
55
Implement **isPerfect ( )** method to check if a binary tree is a **perfect binary tree.**
56
What are **AVL trees**?
Special **types of binary trees** that **self balance themselves**.
They do this by ensuring the right and left subtree difference isn't **greater than one** on each insertion.
The **difference in height** between **left and right sub trees** still equals zero or less than one.
It it's greater than one, **they self-balance using rotations**!
**rotations come up in interviews.**
57
How do **AVL trees work**?
If difference between **left and right tree** is **more than one**, self balance **using rotations**.
58
What does a **perfect tree** look like?
**Every level** is **full with nodes**
Reality?
As we **add and subtract** values some **branches get longer** or **shorter**
59
What happens to **binary trees** **in reality**?
They become unbalanced!
60
What is an **unbalanced binary tree**?
The **right subtree** is taller than the **left subtree** by more **than one**.
61
How do our search trees **become unbalanced**?
**Insert** **sorted values** in **ascending or descending order**!
Right skewed tree.
Sorted in descending order is a left tree.
62
What is a **right skewed binary tree**?
Most nodes have **only right children**
Like **linked-lists**
if **lookup (value)** is in **last node**, **O(n) operation**!
63
What is a **left skewed tree**?
Worst type of binary tree.
Most nodes have **only left children**
Like **linked-lists**
if **lookup (value)** is in last node, **O(n) operation**!
64
What **problem** do **AVL trees solve**?
The **Big-O** of a **binary search tree** dropping from **O(log n)** to **O(n)** due to **improper structuring.**
**How?**
Only a **balanced tree** performs at **logarithmic time complexity**.
We cannot have a **long branch**.
**Right, left skewed** trees are like linked lists lookup (value) = **O(n) operation**.
**How?**
Self-balancing mechanism
65
What **is an AVL interview question?**
**Add integers** in a **binary tree**
**show** where **imbalanced**
show **how to rotate** (draw on whiteboard)
66
What **are the four types of rotations**?
The type of rotation **depends** on what **side of the tree** is **heavy**
67
When do we **perform a left rotation**?
When the tree is **heavy on the right**
How?
**height** of **left increases** by **one (**becomes **left child)**
**height** of **right decreases** by **one**
**Calculation:**
**balanceFactor = height (L) - height (R)**
**balanceFactor** \> 1 **| left heavy** **(right rotate)**
68
When do we perform a **right rotation**?
When **tree is heavy** on the **left side**
**height** of **right increases** by **one (**becomes **right child)**
**height** of **left decreases** by **one**
**Calculation:**
**balanceFactor** = **height (L)** - **height (R)**
**balanceFactor** \< **-1** | **right heavy** (**left rotate**)
69
AVL When do we perform a **left-right rotation**?
imbalance in **left-child** (**left rotation**) **right-subtree** (**right rotation**)
70
AVL When do we perform a **right-left rotation**?
When imbalance in **right-chi**l**d** (right rotation) **left-subtree** (left rotation)
71
**Set:** 1, 2, 3, 4, 5
Add the **set of numbers** to an AVL tree.
1. **Start** with an **empty tree**.
2. **Draw** the tree at **each step**.
3. **Show** the **type of rotations** required to **rebalance** the tree.
72
**Set**: 5, 10, 3, 12, 15, 14
Add the **set of numbers** to an **AVL tree**.
1. **Start** with an **empty tree**.
2. **Draw** the tree at **each step.**
3. Show the **type of rotations** required to **rebalance the tree.**
73
What is the solution **part one**?
**Set:** 12, 3, 9, 4, 6, 2
Add the **set of numbers** to an **AVL tree.**
1. **Start** with an **empty tree.**
2. **Draw** the tree at **each step.**
3. Show the **type of rotations** required to **rebalance the tree**.
74
What is the **solution** **part two**?
**Set**: 12, 3, 9, 4, 6, 2
Add the **set of numbers** to an **AVL tree.**
1. **Start** with an **empty tree.**
2. **Draw** the tree at **each step.**
3. Show the **type of rotations** required to **rebalance the tree.**
75
What is a good resource for **visualizing trees**?
https://www.cs.usfca.edu/~galles/visualization/AVLtree.html
76
How do we implement the **insert ( ) method** using recursion in our AVL tree?
**A public method to kick off recursion.**
* In public method call the method and give it root, value
* set root to object that is returned from private AVLNode
**A private method to run recursion.**
* one scenario is when tree is empty! Return AVL node and set to root in public method
* not empty, go right or left depending on value
77
AVL How can we **re-write** this **helper method** using the **ternary operator**?
78
How can we refactor the **isBalanced ( )** method in our **AVL tree**?
**Private helper methods:**
## Footnote
**isLeftHeavy ( )**
**isRightHeavy ( )**
**balanceFactor ( )**
79
AVL How do we refactor the **balance ( )** method?
extract into a **private helper method**
80
What is pseudo-code for detecting what kind of rotation is needed on a right heavy tree?
81
How do we implement **rotateRight ( )** and **rotateLeft ( )** methods?
82
How do we refactor the **balance ( )** method to **implement rotations**?
83
AVL how can we refactor **setHeight ( )** method?
Extract logic into a **separate private helper method**
84
How do we refactor the **insert ( ) method** in our **AVL class**?
extract logic into **private method**s:
setHeight ( )
balance ( )
85
What is a **heap**?
A **complete binary tree** that satisfies **the heap property**
1. **Complete binary tree** - all levels are full, **nodes inserted** from **left to right**
**2. Heap property -** value of **every node** is **greater than or equal** to **children**
86
What is a **complete tree**?
**Yes.**
Every **level is completely filled** with **nodes**
Last level could **have a hole**
Levels filled **left to right**
87
Is this a **complete tree**?
**No.**
Nodes are filled left to right
**Missing** a **left node** in last level
88
What are the **applications of heaps**?
Many **applications** like in **sorting and graph algorithms**.
1. **Sorting data** (HeapSort)
2. **Graph Algorithms** (the shortest path between two nodes) - powers GPS
3. **Priority Queues**
4. Finding **Kth smallest/largest value** - popular interview question
89
Is this **tree complete**?
No.
**Second level** is **missing a node**!
90
What is a **binary** **max heap**?
**Root node** holds **largest value**
Children are less
largest value bubbles up to root
91
What is a **min heap**?
Root holds **smallest value**
Children are all larger
smallest values bubble up to root nodes
92
What are the **heap operations** and **run time complexities**?
**remove ( )** - **O (log n)**
removing largest value in a heap
where log n = height of tree
**insert ( )** - **O (log n)**
insert in leaf node, bubble up is log n operation.
**max ( )** - **O(1)**
return root in max heap
**min ( )** - **O(1)**
return root in min heap
**Bubble ( )** - **O(log n)**
moving a node value up to the root value to maintain heap property or swapping nodes until a value is in the right position to maintain valid heap.
\*O(h) where **h = height = log n**
93
What is **bubbling up**?
**Moving node**s up **the heap**
**Swapping** with **parent**
94
Insert the **numbers in a heap** and **draw each step** then remove 24 and draw bubble steps.
95
Insert the numbers in a heap and draw each step then remove 24 and draw bubble steps.
96
Insert the numbers in a heap and draw each step then remove 24 and draw bubble steps.
97
Insert the numbers in a heap and draw each step then remove 24 and draw bubble steps.
98
Insert the numbers in a heap and draw each step then remove 24 and draw bubble steps.
99
What **data structure** do we use to **create a heap**?
**An array**
We get the **index** of **right and left children** in the array using the **formula**:
**left** = parent \* 2 + 1
**right** = parent \* 2 + 2
**parent** = (index - 1 ) / 2
100
HP How do we **refactor** the **insert ( )** method in our **Heap class**?
Extract the **bubbleUp ( )** method
into a private method
101
How do we implement the **bubbleUp( )** method in our Heap class?
102
HP How do we implement **remove ( )** method in our Heap class?
Using private helper methods:
## Footnote
**largerChildIndex ( )**
**isValidParent ( )**
**rightChild ( )**
**leftChild ( )**
**rightChildIndex( )**
**leftChildIndex ( )**
103
What is the **edge case** issue with our **largerChildIndex ( )** method?
How do we know if the **node has children**!
use **helper methods**:
**hasLeftChild** ( )
**hasRightChild** ( )
104
What is the **edge case issue** with the **isValidParent ( )** method?
**Assumes** node has **left** and **right** **nodes**!
105
HP How can we refactor our **remove ( )** method?
Extract **bubbleDown ( )** logic into a **private method**
106
What is **heapSort ( ) ?**
Using a heap to **insert values**
remove them in **decending order** (**max Heap**)
**Why?**
remove method **removes root (max value)**
next largest value **bubbles up**
continue removing the **largest numbers in heap**
107
How do we sort in **ascending** ordering using **heapSort ( )**?
Change **loop direction**
108
When is it **best** to use a **heap** to build a **PriorityQueue**?
For **many inserts (enqueue) operations!**
**PriorityQueue** using **an array:**
**insert ( ) aka enqueue ( ) - O (n)**
Have to **shift items** to insert at sorted index
**remove ( )** **aka dequeue ( )** - **O (1 )**
update the count pointer (count - 1)
**PriorityQueue** using **a heap**:
**insert ( )** **aka enqueue ( )** - **O (log n)**
**bubbleUp ( )** length of tree, **divide and conquer**
**remove ( ) aka dequeue ( ) - O (log n)**
**bubbleDown ( )** length of tree, **divide and conquer**
109
How do we **implement** a **PriorityQueue** using a **Heap**?
**Essentially**, a wrapper around **Heap class**!
110
How can we refactor our **heapify ( )** method?
**Popular interview question:**
**transform** **an array** into **a heap in place**
**Optimization:**
**lastParentIndex** - only heapify parent nodes (**not leaf nodes**)
**i = lastParentIndex** - start recursion at deepest parent nodes (**reverse recursions**)
111
How do we implement **getKthLargest ( )** using a Heap?
**Popular Interview Question**:
Return the **kth largest item** in a list
**Solution**:
add items to heap
remove items until k - 1
return root (maxHeap)
112
How can we implement **isMaxHeap ( )** to determine if a given **array of integers** represents a **max heap**?
113
How do we implement **MinHeap** using an **array of nodes**?
See MinHeap
114
How do we implement **MinPriorityQueue** using a **Heap**?
115
What are **Tries**?
**Trees** BUT **not binary trees**.
**Each parent** can have **multiple nodes**.
Powerful, **overlooked data structures**
aka
"**Digital, Radix, Prefix trees**"
116
T What is **an application** for **Tries**?
**Auto-completion**
Why?
**Not duplicating** **prefixes**
Can **extend branches**
**each node can have up to 26 letters!**
**Empty root (could be any letter)**
117
What are the **various operations** and **run time complexities** for **Tries (Prefix, Radix, Digital)**?
**lookup ( )** - **O(L)**
walk down tree length of word (L)
**insert ( ) - O(L)**
walk tree, if character doesn't exist, add it
**remove ( )** - **O(L)**
\*L is the length of the word in the Trie.
118
**How** do we **implement** the **TrieNode** using a **hash table** as **children**?
**Create services**:
**hasChild** // returns boolean
**addChild** //adds key-value
**getChild** //returns value
**getChildren** //returns array []
**hasChildren** //returns boolean
**removeChild** //returns void
119
How do we implement **insert ( )** in our Trie class?
120
**How** do we implement **remove ( )** in our **Trie class**?
121
**How** do we implement **contains ( )** in our **Trie class**?
122
**How** do we **implement** **contains ( )** **recursively**?
123
**How** do we implement **findWords ( )** in our **Trie (Autocompletion)**?
124
**How** do we **implement** **countWords ( )** in a **Trie**?
125
T **How** do we implement **longestCommonPrefix ( )** in a **Trie**?
We add these **words to a trie** and **walk down the trie**.
If a node has **more than one child**, that's where these **words deviate.**
**Try this** with "can", "canada", "care" and "cab". **You'll see that these words deviate** after "ca".
So, we **keep walking down the tree** as long as the current node **has only one child**.
**One edge case** we need to count is when **two words are in the same branch** and **don't deviate.**
For example "can" and "canada".
In this case, we **keep walking down** to the end because every node (except the last node) **has only one child.**
**But** the **longest common prefix** here should be **"can",** not "canada".
So, we should find the **shortest word in the list first**.
The **maximum number of characters** we can include **in the prefix** should be equal to the **length of the shortest word.**
126
How do we implement the **TrieNode** class in our **Trie class using an array**?
**fieldOne:** Char value
**fieldTwo:** TrieNodes [ALPHABET\_SIZE] children
**fieldThree:** boolean isEndOfWord
**Space complexity?**
Every node has a **26 element array**
this wastes **a lot of memory**!
127
How do we implement the **Trie class** using an **array for storing characters** in each node?
128
How can we refactor our **TrieNode** implementation **using abstraction**?
Create **services in TrieNode class**
129
What is **pre-order** traversal in a **Trie**?
visit **each root node first**
**then**, visit **children**
**Why?**
**Print all words in Trie**
130
What is **post-order** traversal in a **Trie**?
Visit **children (leaf) nodes** first
then, come up to **visit root (parent) nodes**
**Why?**
**Delete** a word!
Start with **leaf nodes**
131
**How** do we implement **pre-order traversal** in our **Trie class**?
**Why?**
Print **all words** in Trie
132
**How** do we implement **post-order traversal**?
**Why?**
**Delete a word!**
Start with **leaf nodes**
133
How do we **remove a word** from a **Trie**?
**Post-order traversal** (begin at **leaves**)
remove **isEndOfWord marker**
**if (!hasChild) remove it from Trie**
134
What are **graphs**?
**Versatile data structures**!
Consists of **nodes (vertices) and edges**
**Nodes** are called **vertices** (vertex).
**Nodes** can be **connected** to **any other nodes**.
**Directly connected nodes** are called **adjacent nodes**.
**Connections** between nodes are **called edges**
**Edges** can **have weights** to determine **weight of connection**.
.
135
**What don't** we have a **limitation on in graphs**?
We **don't have a limitation** on how **many connections or edges** a node can **have with other nodes**.
136
What are **nodes** called in **a graph**?
**Vertices**
137
What are **neighbors**?
Two **directly connected** nodes
**adject vertices (nodes)** in a **graph**
**Ex.**
**John & Bob** are **neighbors**
138
What are **directed-graphs**?
If **edges** have a **direction**
**Ex. Twitter**
**Follow someone**, they **don't follow** **back**
139
What are **directed** and **undirected graphs**?
**Directed** - following someone in twitter or instagram **Undirected** - facebook friends.
140
What are **real-world applications of graphs**?
**Anywhere** we want to **model relationship** between **objects**!
**Social networks** - finding best friends (**weights on edges**)
**GPS** - **shortest path** between **two nodes**
**find connections** to other **objects in a network**
represent **routers** connected **in a network**
141
**What** is the **adjacency matrix**?
A way to see how **nodes are connected**
Using a **2D array** to represent edges in a graph
**O (n^2)** space complexity
142
What is the **adjacency List?**
An **Array of linkedLists (to represent connections)**
**Every element** in the array has a **LinkedList (bucket)** containing **adjacent nodes** **(neighbors)**
**HashTable** to **find index** of a **vertex (node)**
143
What is the **runtime complexity** of **various operations** using **matrix vs. list** approach in **graphs**?
**K** represents **nodes** in **linkedList**
**V** represents **nodes** in the **graph**
**E** represents connections **(edges)** in a graph
**AddNode** - don't have to **create a new array** and **copy elements** in list
144
**Which approach** is better **(matrix vs. list)** in **implementing a graph**?
**Worst Case scenario (dense graph)**:
Use **Adjacency Matrix**
addEdge, removeEdge, queryEdge
**Most applications (not very dense)**:
Use **Adjacency List**
addEdge, space complexity
145
What is a **dense graph**?
A **hypothetical** (worst case):
When **every vertex (node)** is **connected** to **every other node (beside itself)**
146
**How** do we implement **addNode ( ),** **addEdge ( )** and **Node** class in our **Graph**?
147
How do we implement **removeNode ( )** and **removeEdge ( )** in our **Graph class**?
148
**What** is the **difference** between **traversal** in a **graph vs. a tree**?
There is **no root node** (**can start anywhere**)
the **traversal ends** when the **node** has **no further connections (neighbors)**.
**Other nodes** are **not visited** = there **isn't a path** to those **nodes**.
149
What is the breadth-first graph traversal algorithm?
Visit a node and all it's neighbors before going far in a graph.
150
**How** is the **breadth-first** graph **traversal algorithm** **implemented** in software?
Using **a queue**.
The **queue** holds the **address of the next node** to visit **(neighbor nodes)**.
As **nodes are visited**, **neighbors are added** to **the queue** to visit next.
**Formula**:
**Visit the node**, add **its neighbors to the queue** and **continue** until **there are no neighbors** (connections) left.
151
**When** does the **breadth-first** graph **traversal algorithm** end?
**When** the **queue is empty**, the **traversal is complete**.
**As soon,** as the **queue is "empty"** the **algorithm will stop**.
152
**How** do we implement **traverseDepthFirst ( )** using **recursion** in our **graph**?
Use a **set** (check if visited **neighbor nodes**)
153
What is the "**call stack"**?
**Java Runtime environment** stack
remembers **values of arguments** between **method class**
154
**How** do we implement **traverseDepthFirst ( )** using **iteration**?
**Go deep**, **then loop** to **other neighbors**
Use a **Stack**: neighbors
**Why?**
determine which node to **visit next**
Use a **Set** : visited nodes
**Why?**
To s**kip re-visiting** already **visited neighbors**
155
**How** do we implement **traverseBreadthFirst ( )** in our **graph**?
We **visit a node** and **all it's neighbors** before **moving away** from **the node**
**Using**:
**HashMap** - nodes, adjacency list
**Queue** - storing neighbor nodes (visit next)
**Set** - comparing queue w/ visited nodes
156
What is the **topological sorting** algorithm?
**Common Interview Question**:
**Implement** the **topological sorting algorithm**
Implementation:
**Depth-first traversal,** find nodes **w/out edges**
these are **nodes w/o depenencies (toward end)**
**Top hierarchy (nodes w/ edges) first!**
157
**What** are the **applications of topological sorting** in **graphs**?
**Help** us **determine** which order **we should perform** the **tasks** to **ensure all dependencies are met**.
When you have **multiple tasks** that **have dependencies** on **each other** to be completed.
158
**What** must we know about **topological sorting algorithms**?
**1. Different ways** to **topologically sort** the **same graph**
**2. Only work on graphs w/out a cycle** (must be **directed-acyclic graphs**)
159
How do we implement the **topological sorting algorithm** in **software**?
Using a **stack, a set** and a **for loop.**
Go deep into the graph to find the nodes that **don't have outgoing edges (children)** then work our way up **adding the node to our stack** only **if we have visited all the children** or edges of the node.
1. **Depth-first traversal** to go deep into the graph and find the node **without any outgoing neighbors.**
2. **Add node to a stack** then move up the tree
160
**How** do we **detect a cycle** in a **graph**?
**Interview Question:**
Write code to detect a cycle in a graph using colors!
red, blue, green = all, visiting, visited
**Note:**
Topological sorting doesn't work on graphs w/ cycles!
**Implementation**:
Use **three sets**!
**Set all** - nodes in graph
**Set visiting** - nodes visited but not all children
**Set visited** - nodes visited and all children
**HashTable to print cycle**!
161
**How** do we implement **hasCycle ( )** using **recursion** in our **Graph class**?
**Interview Question**:
Write code to detect a cycle in a graph using colors!
**Implementation:**
Use **three sets!**
**Set all** - nodes in graph
**Set visiting** - nodes visited but not all children
**Set visited** - nodes visited and all children
162
G **What** are **weighted graphs**?
Graphs whose **edges have weights**
## Footnote
**Weights can represent anything!**
**Cost, distance, complexity, anything!**
163
**What** are common **applications of weighted graphs**?
Finding the **shortest path** between **two nodes**!
**GPS** - weights could be traffic, vertices locations!
164
**How** do we implement a **weighted grap**h using a **non-OOP approach**?
**Two private classes:**
Node, Edge
**Two Maps:**
HashMap nodes
HashMap\> AdjacencyList
165
G How do we **refactor** the weighted Graph into an **OOP approach**?
Replace **HashTable\> adjacencyList** with **ArrayList** embedded into **HashTable nodes**
**Add services: addEdge**, **getEdges** to node
Why?
**Object-Oriented Approach** (not taught in Data Structures Textbooks)
Store **edges** in **node objects**
166
What is **Dijstra's shortest path algorithm**?
**Greedy algorithm** for getting the **shortest path** between **two nodes on a graph.**
Uses a **table** w/ assumptions
Calculate dist to **start node** and **neighbors**
find **shortest path**, record node to get there
167
How do we **implement** **getShortestDistance ( )**?
**Dijastras algorithm!**
**Implementation:**
**NodeEntry** class w/ constructor
**PriorityQueue**
**HashTable** distances
**Set** visited
**Breadth-first** traversal (look at all neighbors)
How?
A weighted graph is used.
A **HashMap** is created with distances between one nodes and the other nodes.
The distance to the other nodes are **unknown and initially set to a large value** (Integer.MAX\_VALUE)
As we move along the graph the **distances are updated in the table as shorter paths are found**.
The **PriorityQueue** helps us move to **next closest neighbor (greedy algorithm)**
168
**How** can we refactor the **getShortestPath ( )** in our **WeightedGraph** **class?**
Extract **buildPath ( )** into a **private method**
169
What is a minimum spanning tree in a graph?
We can convert a graph to a min spanning tree by calculating the min distance between nodes and removing all but that one edge between nodes. Should have n-1 edges. Using Prims algorithm can find the minimum spanning tree
170
**How** do we represent **how strong a connection** is **in a graph**?
With a **weight.**
Edges can **have a weight.**
By **measuring interactions** between **nodes** we **can assign higher weights.**
