Algorithms Flashcards
What key algorithms does this course explore?
Search, Sort, String Manipulation
These algorithms up in software engineering interviews all the time!
What distinguishes an average programmer from an outstanding software engineer?
Understanding how search, sort and string manipulation algorithms work and evolved distinguishes an average programmer from an outstanding software engineer!
Why?
Libraries and frameworks helps us sort data without knowing how sorting or searching algorithms work!
So…
That’s why sorting algorithms come up in interviews all the time!
Action:
How they work, Time & Space complexity, implementation
What algorithms run in good Big-O?
algorithms that run in green or yellow!
What are the seven essential sorting algorithms all software engineers must know?
- Bubble Sort
- Selection Sort
- Insertion Sort
- Merge Sort
- Quick Sort
- Counting Sort
- Bucket Sort
What must we be able to do with sorting algorithms?
Explain how each algorithm works
Know each algorithm’s time and space complexities
Implement each algorithm in given language of choice (Java)
What is bubble sort?
sort in increasing order (ascending order)
scan array from left to right, if out of order, swap
if right is smaller than left, swap them
requires multiple passes (iterations)
next largest number moves to correct position
What is the Big-O for bubble sort?
Best case = already sorted
worst case = reverse sorted
O(n) * O(n) = quadratic (worst case)
O(n) = linear (best case)
passes = each pass bubble one number into place
comparisions = bubbling into place
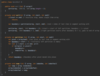
How do we implement bubbleSort( ) in Java?
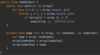
How can we optimize our implementation of bubblesort( )?
reduce O(n) iterations if sorted!
compare only unsorted items by not comparing last items (bubbled up items)
What is selection sort?
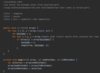
ascending order (smallest to largest)
Multiple passes over an array
In each pass we select the minimum value (from unsorted part) and swap this index with next index(in sorted part).
What is the time complexity of the selection sort algorithm?
O(n) * O (n) : Quadratic
Fairly slow algorithm!
iterate array = O(n) operation!
iterate unsorted array = O(n) operation!
next min value - iterate unsorted part = O(n)
How do we implement selectionSort ( ) using java?
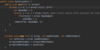
What is insertion sort?
each iteration pick one value from unsorted part, insert into sorted part (shift, make space)
Insert how?
We copy the values in the sorted part to the right to make space, then insert the value into the correct position.
Current (unsorted min value) is compared to all values in sorted part.
greater values are shifted to make space.
What is the key difference about insertion sort vs. bubble sort and selection sort?
instead of swapping items, we shift items in our array to the right
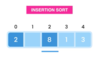
What is the Big-O for insertion sort?
O (n) * O (n) - quadratic
(worst case)
Same as bubbleSort( )!
How do we implement insertionSort( ) in java?
What is merge sort?
n (log n) time complexity!
Why?
It’s a type of algorithm called “divide and conquer algorithm.”
How?
it works by breaking the problem down into recursively smaller problems that are easy to solve.
Then it merges those solutions to get the final result.
How does merge sort work?
dividing and conquering!
break array at middleIndex
divide again at middleIndex (left subarray)
divide again at middleIndex (right subarray)
keep breaking down the array into smaller subparts.
Until, cannot divide anymore
Then compare subparts and merge (sorted)
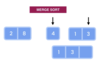
What is the Big-O of the merge sort algorithm?
Time complexity:
O(n log n) operation!
O (log n) - dividing into subparts
O(n) - read each item, merge subparts
Faster than quadratic!
Space complexity:
O (n) space!
Don’t need to re-create arrays for merge, reuse
How do we implement MergeSort algorithm in Java?
How do we implement a base condition to stop recursion in merge sort?
if their is one item in the array only!
What is partitioning?
How we move items around a pivot
How?
select last item as pivot
rearrange other elements around it
using two pointers
i = iterate over array (loop variable)
b = boundary (end of left partition)
if the item is smaller than the pivot…
increase boundary (left partition), we swap lower value into left partition
What is the quickSort algorithm?
One of the most used sorting algorithms
built into many frameworks and languages
Why?
sorts an array in place without additional space.
O (log n) average time complexity!
How?
first, select a pivot
re-order the items around this pivot (partitioning)
items on right are larger than pivot
items on left are smaller than pivot
Pivot is now in place (doesn’t move)
select next item as pivot
partition again
What is the Big-O of the quick sort algorithm?
Why?
O(n) - have to iterate all items and swap (partitioning)
# of times can partition - depends on pivot selection
w/ the right pivot selection on average can run in
O(log n) time
How do we implement the quickSort algorithm?
What are comparision based sorting algorithms?
They sort data based on comparision
What are non comparision sorting algorithms?
They use basic math to sort
What is count sort?
non comparision sorting algorithm
we count occurrences and use that to sort data
How?
allocates a separate counts array
iterates input array, updating counts array
iterates counts array, sorting input array
When should we use count sort?
values must be positive to use as index in counts array
if input range has gaps, will end up with many 0s in counts array
What is the Big - O of counting sort algorithm?
O(n) time complexity!
faster than O(n log n)
Why?
Space - O(k) where k = max range of input array
Populate counts array - iterate input array O(n) operation!
iterate counts array, refil input array = O(n + k)
Cost?
time-memory tradeoff!
allocating extra memory!
How do we implement the counting sort algorithm?
O (n) time complexity
O(k) space complexity!
What is the bucket sort algorithm?
iterate input array, dividing items into buckets
iterate buckets, sort each bucket using sorting algorithm
merge buckets
can sort buckets in parallel
each item in the bucket is a linked-list
What is Big-O of bucket sort algorithm?
Range: O(n) to O(n^2)
single bucket (worst case) - O(n^2) using insertionSort on buckets
many buckets each a single item (best case) - O(n) time complexity but at a memory cost
How can we refactor bucketSort to make it cleaner?
What are the five essential searching algorithms all software engineers must know?
These come up in coding interviews!
Understand how it works!
Understand its Big-O!
There are more searching algorithms but these five come up in coding algorithms!
Five algorithms:
- Linear Search - O (n)
- Binary Search - O (n)
- Ternary Search - O (n)
- Jump Search - O (n)
- Exponential Search - O (n)
What is Linear Search?
Simplest search algorithm.
relatively slow O(n) operation!
works well with a small list!
How it works:
Iterate over a list
inspect items, if value matches search, return it
otherwise return -1
How do we implement linear search in Java?
What is binary search?
Divide and conquer algorithm
O (log n) operation!
In each step, we cut the number of items to inspect by half!
First, calculate middle index
Next, item is either on left or right side of partition
Repeat, calculate middle index
Stop, index = value
What is Big-O for binary search?
O(log n) time - divide and conquer algorithm
O(log n) space - recursive calls on stack
O (1) space - iteration implementation
How do we implement binary search using recursion?
How do we implement binary search using iteration?
What is ternary search?
divide list into three parts (partitions) recursively
partitionSize = (right - left) / 3
midPointOne = left + partitionSize
midPointTwo = right - partitionSize
compare these index values to our search value
if not a midPoint, could be in partition, recursive part
eventually, the method will return the index of search value!
What does the logarithm function tell us?
To which power to raise a number to get another number
Ex.
Log base 2 of 8
tells us what power to raise two to get eight!
To which power should we raise 2 to get 8?
Answer 3.
What is the Big-O of ternary search?
As we divide our list into more parts, search algorithm gets slower!
Binary search is faster than ternary search!
Why?
Worst case scenario a list of 10 items has 10 partitions, O(n) have to compare value to every item in list
How do we implement ternary search using recursion?
What is jump search?
Divide list into blocks (blockSize = squrt(n))
jump to that block where value may exist
How?
Compare last item in block with target value
if value is greater, jump to next block
When?
value is less than last item in block
do linear search in that block
What is the Big-O of jump search?
O( squareroot(n) )
An improvement to linear search!
Not as fast as binary search!
How do we implement jumpSearch in Java?
How do we refactor this code in jumpSearch?
Add the conditional statement to the while loop
What is exponential search?
Start w/ small range
check if target is w/in range
if it’s not, double the range.
check if target is in this range.
if target is potentially w/in range
do a binary search w/in range (after upper bound of previous range)
What is Big-O of exponential search?
O ( log i )
i = # items in range
How do you implement exponentialSearch in Java?
What are the string manipulation algorithms?
- Find the number of vowels in a string
- Reverse a string
- Reverse the order of words in a sentence
- Check if a string is a rotation of another string
- Remove duplicate characters in a string
- Find the most repeated character in a string
- Capitalize the first letter of each word in a sentence
- Detect if two strings are anagrams (contains exact same letters in any order)
- Check if a string is a palindrome. (If we read palindrome string left to right get same letters).
What are some useful Java classes/methods for solving string manipulation excercises?
How do we implement countVowels ( )?
How do we implement reverse ( ) to reverse a string?
How can we reduce the time complexity of reverse ( ) from O(n^2) to O(n)?
Use the java class StringBuilder to create mutable strings
eliminates O(n) for creating a new string everytime we add a letter!
What’s another implementation of reverseWords ( ) using built in Java functions?
How do we implement reverseWords ( )?
How do we implement areRotations ( )?
If this string is one million characters the space complexity is very large therefore we need to implement this method using a for loop to compare values!
What is a different way of implementing areRotations ( )?
How do we implement removeDuplicates ( )?
How do we implement getMaxOccuringChar ( ) w/o using a HashMap <> ( )?
Can use an array
Store each character at ASCII value as index
increment value at ASCII index
How do we implement maxOccurringChar ( )?
How do we implement capitalize ( )?
Popular Interview Question!
Edge cases:
whitespace front / back - . trim
whitespace between words - .replaceAll w/ single space
pass empty space - .isEmpty, return empty string
How do we implement isAnagram ( ) using sorting?
Very popular Interview Question!
ask if solution must be case insensitive
Edge cases:
pass empty string
pass white space
pass null - check
SM How do we implement isPalindrome ( )?
