STATS Lec 2- Normal distribution and Z scores Flashcards
1
Q
Frequency distribution
A
- Useful to show data
- X = categories
- Y= frequency category occurs
2
Q
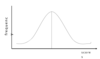
Characteristics of a normal distribution
A
- Bell-shaped
- Symmetrical
- Tails of the distribution never meet the X-axis
- Is mathematically defined
3
Q
Measures of dispersion: Kurtosis
A
- Kurtosis is a measure of dispersion/shape of a frequency distribution
- Relates to how peaked or flat a distribution is
- Flat distributions: ‘Platykurtic’ (not a lot of difference between the lowest and highest points)
- Peaked distribution: ‘Leptokurtic’
- A normal distribution is ‘Mesokurtic’
4
Q
Measuring variability of data
A
- How variable is the data?
- Easy if we are using the normal distribution
- Variance: a mathematically defined measure of the variability of data (a spread of data about the mean)
- A measure of how much the data vary around the mean-
- Mean of the squared deviations from the mean
5
Q
Variance=
A
- Bell-shaped distribution
- Variance is a measure of how far each individual point is from the mean
6
Q
Formula for variance
A
- Variance is the mean value of the squared deviations from the mean
- HOW to calculate:
- X = make individual measurements
7
Q
Calculating variance
A
- Next calculate the MEAN of the data set
- u= population mean
- Next, calculate the distance each data point is from the mean
- X-u
- Then square (to get rid of direction)
- (X-u)2
- Then divide by N
8
Q
What does variance tell you
A
- A measure of how far each individual data point is from the mean
- A measure of variability or spread
- Which of these sets has a greater spread of data
- Which data set has the greatest spread
- = u= 80 and sigma2 = 50
9
Q
Standard deviation
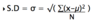
A
- Is another measure of the variation of the scores around the mean
- The square root of the variance
- In the normal distribution, 68% of the scores lie within one SD
- 95% lie within 2 SD
10
Q
A normal distribution
A
*
11
Q
So far
A
- u = mean
- Sigma = standard deviation
- Sigma2 = Variance
- Often expressed as mean (S.D)
- e.g. 63 (2.8)
12
Q
Is a single observation typical of the population
A
- A person gets a score of 125 in a test
- Is this person special?
- Need to know 3 numbers: the mean, standard deviation and the person’s score
- Can we convert this all to just one number or standard score- this is so we can easily answer this question
13
Q
Transform the normal distribution
A
- Exam score on the bottom
- We place mean (100) as 0 (to the left of the mean is negative to the right is positive)
- Take exam score (X) - Mean (u) / Standard deviation (Sigma)
- (125-100 / 10)
- This will give us our SD around the mean = Z score
14
Q
Is a mark of 125 special
A
- Convert this in the same way
- Z = X-u / sigma
- Z= 125-100/ 10
- Z= 2.5, therefore 2.5 SD away from mean
- 125 = 2.5 SD from the mean so 125 is a very good mark
15
Q
Z scores
A
- If you were to choose a person at random, how likely would it be that their Z score was
- Between -1 and +1- 68%
- Between -2 and +2- 95%
- Bigger than +2
*
16
Q
BUT
A
- Parametric statistics only work when you have a normal distribution
- Clearly biphasic so not normally distributed- so no Z scores
18
Q
Positive skew
A
- Majority of data on left hand side of frequency distribution
- Falls down left to right
- No parimetric
19
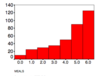
Q
Negative Skew ›
A
- Most of the data on the right-hand side
- Rises from left to right
20
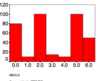
Q
Bi-modal
A
21
Q
Another problem: outliers
A
- Outliers are far away from body of the data
- Mean will have a big effect on mean
- We should look at outliers to see if they are anomilies
