STATS 13- ANOVA Flashcards
1
Q
Reminder: normal distribution
A

2
Q
What do Z and t tell you
A
- z tells you how different an individual was from the group
- t tells you how different the means of 2 groups are

3
Q
Do you need analysis of variance (ANOVA)
A
- t-tests: compare 2 groups
- ANOVA: compare as many groups as you like
- Better description: analysis of variance of group MEANS
- Looking at variability between and within group
4
Q
ANOVAs and t-tests
A
- What happens when you have more than 2 groups (A, B, C, D)
- We need to be able to see where the overall variability comes from (e.g. A may be very different to BCD)
- Why not just do lots of t-tests?
- Massively increased probability of accepting something as different when it is not
- Every time we do a t-test we accept there is the probability that it is due to chance, the greater number of t-test we do this chance accumulates
- Get lots of possible combinations
- A-B, A-C, A-D, B-C, B-D, C-D
5
Q
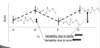
ANOVA
A
- F= Variability due to factor (means) / Variability due to error
*
6
Q
Sources of variation
A
- The important this to realise is that you can divide the variability of a set of data into
- A: variation BETWEEN groups
- The effect of the FACTOR
- Calculate the mean square between groups
- B: variation WITHIN groups
- The ERROR
- Calculate the mean square within groups
7
Q
F value and Jargon
A
- F= Variability due to factor (Sb2) / Variabiltiy due to error (Sw2)
- Mean square (S) is the same as variance (sum squares/ df)
- Sum of squares (SS) is just another measure of variability
8
Q
Degrees of freedom
A
- For the ANOVA we’re making 2 estimates: variability due to factor (IV) and variability due to error
- The significance of an F value, just like t, depends on the number of measurements or degrees of freedom (DF)
- So when quoting ANOVA resulting need to give 2 degrees of freedom values
- Between groups, DF, then WITHIN groups DF
- k-1, N-k
- k= Number of groups
- N= total data set
9
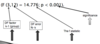
Q
Reporting results
A
- We found that the choice of lecturer had a significant effect on final exam scores
- (3,12) = df: 3= df due to factor; 12=df due to error
- Highly significant difference between the scores
*
10
Q
ANOVA summary from SPSS
A
Mean square = Sum of squares / df
F = Mean square (factor)/ Mean square (error)

11
Q
ANOVA between-subjects design
A
- Differences between participants make up a large portion of the error term
- The effect of the factor has to be large before it is significant
- Low statistical power (probability of rejecting a false null hypothesis is low, see lecture)
- Sample sizes, or effect size, need to be large to be detected
12
Q
ANOVA: within-subject design
A
- Every participant is tested in each condition
- Differences used: removes between- subject (not very interesting) variation from the error term
- Small factor (IV) effects are more likely to be detected as significant
- High statistical power
- Fewer participants needed


