STATS 17- Non-parametric 2

Question 1

Testing difference- Non-parametric tests

Answer 1

• Mann Whitney U
• Kruskall-Wallis
• Friedman’s

Question 2

Mann-Whitney U Test

Answer 2

• Subjects Design: Independent groups/ Independent measures design
• Description of tests
  
  • RANKS data
  • Counts the number of time one condition is ranked higher than the other
  • Calculated statistics (U) is the sum of the number of times values in the first group are higher than values in the second group

Question 3

Calculation of “U”

Answer 3

• Rank all of the scores together (as if from one group)
• Add up ranks from the smallest group (or either if both groups are the same size) =R
• N1= Number of cases in smallest group
• N2= Number of cases in the largest group

Question 4

Example

Hypothesis: drinking alcohol the night before an IQ test will affect people’s scores

Answer 4

Question 5

Example continued

Answer 5

• Use the smaller value of U and compare to the critical values
• U should be equal to or lower than the critical value for significance

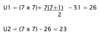
Question 6

Critical values of U

Answer 6

Question 7

Ranks

Answer 7

Question 8

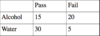
Dichotomous data

Answer 8

• Can’t use Man U for this
  
  • Need to use a chi-square instead- set out as how many people in each condition passed vs. failed (or whatever you are measuring)
• E.G. If passed or failed an exam
• Two conditions: alcohol or water
  
  • Numbers represent the number of people

Question 9

Revision

Answer 9

• 1 way= is data different from what we expect from random variation
• 2 way = main effect caused by each variable and wheather there is an interaction between the 2 variables
  *

Question 10

ANOVA assumption

Answer 10

• Data normally distributed
• Homogeneity of variance
  
  • If assumptions NOT fulfilled use non-parametric equivalent to ANOVA
• Repeated measures design
  
  • Freidmans (q statistic calculated)
• Independent measures
  
  • Kruskal Wallis (K statistics)

Question 11

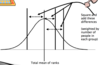
Kruskal-Wallis

Answer 11

• Subject design: Independent groups
• Description: Works by ranking scores across groups
• Expect each group to have a similar mean rank if no difference between them
• Uses squared deviations of mean rank sums from the total mean of ranks (weighted by sample size)
• NB: Can only tell you that at least 2 groups are significantly different- not which 2

Question 12

The logic

Answer 12

• The test works by calculating the squared deviations of the mean rank sums from the total mean of ranks (weighted by sample size)
• The bigger this summed deviation, the more likely the conditions are significantly different
• The summed value is converted to “H” for convenience
• H follows the chi-square distribution- and like chi-square, the bigger the less likely results are due to chance/sampling error

Question 13

Friedman’s

Answer 13

• Subjects design: repeated measures
  
  • Within-subjects
• Description: Changes each individual’s set of scores in the ‘x’ conditions to a rank; so if there are 3 conditions each subject will have rank 1,2,3
• Each subject does each condition, rank the highest score for each condition
• If the null hypothesis is true, the order of the ranks will vary randomly and the sum of ranks for each condition will be approximately the same

Question 14

Example (Continued)

Answer 14

• A measure of dispersion of the rank sums is obtained by summing the squared deviations of the rank sums from the mean rank sum= S
• “S” can then be converted easily to X²r (Is distributed like chi-squared) to assess significance

Question 15

Friedman’s

Answer 15

Question 16

Can you?

Answer 16

• Identify the type of data you are collecting
• Identify the research design you are using
• Choose the correct descriptive statistics to summarise that data
• Select the appropriate test to analyse your data
• INTERPRET the result in the context of the experiment