STATS- Lec 12 T tests

Question 1

Normal distribution

Answer 1

• You can only use t tests that are normally distributed
• (68% = 1 SD, 95% = 2SD)
  *

Question 2

Quick reminder

Answer 2

• Normal distribution
  
  • 60% with 1 SD
  • 95% within 2 SD
• Z scores
  
  • -1 to 1: 60%
  • -2 to 2: 95%
• Need to know
  
  • True mean
  • SD

Question 3

Guinness

Answer 3

• ‘Student’ alias Willian Gosset (1908) was an employee of Guinness breweries
• He was looking for a metric of quality control

Question 4

“Student” realised that

Answer 4

• What if true mean and SD are unknown
• Have to estimate mean (and variability) from a limited number of measurements
  
  • Cannot calculate z scores
  • Creates a “t distribution”
• NUMBER of measurements important
  
  • A large number of estimates (>30) then t distribution is just like z distribution
  • Number of measurements related to “Degrees of freedom” of an experiment

Question 5

Degree of freedom

Answer 5

• This is the difference between the number of measurements made the number of parameters estimated
  
  • A parameter is a value that describes something
• For example
• Estimating the mean (1 parameter) from 5 numbers leaves 4 degrees of freedom in an estimate, the more reliable the estimate

Question 6

T and degree of freedom

Answer 6

• Unlike z, the t distribution depends on the number of degrees of freedom
  
  • Hence t relies on the number of measurements made the number of parameters
• The more degrees of freedom, the closer t comes to z
• If t and z were exactly the same then 95% of data would fall between t = -2 and +2: This only happens when the number of degrees of freedom is 30 or more
• If they are smaller than 30 df than the critical value (t value between which 95% is held) will be greater than 2
• The concept of a CRITICAL VALUES: tcrit

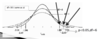
Question 7

Is that t-value significant

Answer 7

• Depends on the Df
• [t] >3.18 Df=3, p<0.05; 5% probability it is not significant
• [t] >2.45 Df=6, p<0.05
• [t] >1.98 Df=30, p<0.05 (same as z)
• The fewer measurements, the larger the t values have to be to reach significance
• small t value unlikely to be significantly different from chance

Question 8

How to calculate a t values

Answer 8

• Independent measures
• For independent samples
  
  • Between subjects design
• t=difference in means/ difference expected by chance
• t= Mean 1- Mean 2 / SD of the means
• Data HAS to be normally distributed

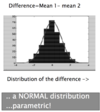
Question 9

The 2 sample t-test visualized

Answer 9

*

Question 10

For repeated measures design

Answer 10

• WITHIN subjects design
• 2 measurements made in EACH subject
  
  • e.g. Before treatment and after
• Calculate CHANGE in EACH SUBJECT
• t= Mean change / Change expected by chance
• Measure the height of a person, measure the height of the same person with socks on

Question 11

The repeated measures t-tests

Answer 11

• Join up scores from the same subject
• Get a list of difference d1,d2…d100

Question 12

Reporting results

Answer 12

• The statistic value (t=1.95)
• Degrees of freedom (df=39)
• Significance level (p<0.025)
• There was a significant difference between the 2 groups (t=1.95, df=39, p<0.025)
• NB. Interpretation of the meaning of that difference depends on the research design

Question 13

Standard error and repeated measures t-test- Visualising data

Answer 13

Question 14

The sample mean

Answer 14

• In practice, you can’t survey everyone in a population
• You take a sample of that population and assume that it is representative
• The sample mean is an estimate of the true population mean

Question 15

But how accurate is your sample mean

Answer 15

• If you were to estimate the mean over and over again what would be the spread
• The standard error (known as the standard error of the mean)
• The standard error depends on two things: the standard deviation of the original distribution and the number of samples

Question 16

Standard error

Answer 16

• How well do you know the mean value
• Depends on how many samples you have
• the standard error is a measure of how close the sample mean is to the true mean
• If you make a number of estimates of the sample mean, 95% of them will be within plus or minus 2 standard errors of the true mean
  
  • Can you think why this is
• As sample size increases the standard error decreases- accuracy increases

Question 17

The 2 sample t-test visualized

Answer 17

• T = difference between means / Pooled standard error
• A = no sigficicant difference

Question 18

The repeated measures t-test

Answer 18

• Re-test the same group of subject
• More sensitive than independent sample tests
• Need fewer subjects
• BUT sensitive to carry-over/ Order effects

Question 19

The repeated measures t-test

Answer 19

• Join up scores from the same subject
• Get a list of differences

Question 20

Distribution of differences

Answer 20

• Null hypothesis: the mean difference will be zero
• The standard error of the mean difference is much smaller than the standard errors of the mean

Question 21

What should you know

Answer 21

• The standard error is an estimate of how reliable a mean value is
• Large number of samples, small standard error
• Repeated measures tests work because they look at the distribution of the differences (which are much less variable)

Question 22

What do z and t tell you

Answer 22

• z tells you how different an individual was from the group
• t tells you how different the means of 2 groups are:

Question 23

What is the standard error

Answer 23

• The standard error is the variability of group means you’d expect by chance
  
  • The more ‘standard errors’ apart 2 mean values are, the bigger the t value, the smaller the p-value
  • Big t = little p = BIGGER significant difference
• Likewise, could define standard deviation as the variability across individuals you’d expect by chance

Question 24

Another look at the t-test

Answer 24

• Variability due to error (poor sampling, poor method)
• Difference due to factor
• t= Difference due to factor/variability due to error