STATS 16- Non-parametric tests Flashcards
1
Q
Why so many different tests
A
- Different data types
- Different experiments have different numbers of conditions
- One way, Two ways
- Different subjects design require different tests, because different assumptions can be made
- Independent vs repeated measures
- Normal vs non-parametric
2
Q
Chi-squared test
A
- One variable chi-squared
- Chi-squared tests of association
- Both calculate the difference between
- OBSERVED frequencies (your data) AND
- EXPECTED frequencies (arising by chance)
- If the difference (O-E) very large: a real effect
3
Q
It’s all greek
A
- X2= Chi-squared
- E= sigma (sum of)
- O= observed value
- E= Expected value
4
Q
Discrimination in the workplace
A
- 6 male managers
- 4 female managers
- Is this discrimination against women?
- Would expect 5 of each sex but the reality is only one person out- most likely just chance
- Due to small numbers can’t say it is due to discrimination
5
Q
Bigger firm: Contingency table
A
- Frequency of male-female managers
6
Q
What might we expect
A
- Chi-squared divides each difference squared by the expected frequency and sums them all- this is the value of chi
- If the differences are larger, chi will be larger= more likely to be a trend as oppose to chance
- X2= 100/50 + 100/50 = 4
- The value of 4 (chi) is our CALCULATED STATISTIC in this case (p<0.05)
7
Q
What a computer would do for us
A
- 60 men
- 40 women
*
8
Q
One variable chi square test
A
- Throwing a die on the following numbers with the following frequencies
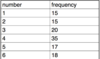
9
Q
Interpreting the output
A
- Because p value= <0.05 (0.013) we can say there is a significant difference between what we expect and what actually happened with a Chi2 value of 14.4
- NB- for Chi2 to be valid, the observed frequency in each cell of a contingency table must be at least 5
*
10
Q
Is it significant?…see more later
A
- Compare your CALCULATED STATISTIC
- t…From t-test
- f…From ANOVA
- X2…chi-squared test
- Compare with
- A CRITICAL VALUE
- In a stats table
- A computer does it for you
- Usually for different df, and different levels of confidence (5%, 10%)
11
Q
The sign test
A
- The simplest but least powerful test for a difference between 2 conditions
- Subject design: repeated measures
- Description: Counts the number of times one conditions is larger than the other and compares this number to what would be expected by chance
- NB: need at least 6 pairs of scores
12
Q
Calculation of the sign test
A
- Discard people who scored the same in both conditions (discard pairs)
- Count how many scored more in 1st condition and how many scored less in 1st condition
- Take the lower number from 2
- If the result is equal or less than the critical value for the number of people in the experiment, THERE IS A SIGNIFICANT DIFFERENCE
13
Q
Example
A
- Hypothesis: there will be a difference between IQ scores between the first and the second time to take the test
14
Q
Use of sign test
A
- Generally only when the direction but not the size of the difference is important
- Does not give information about size of difference
- Can handle Dichotomous data (nominal data)
- (Only 2 possible values) e.g. yes/no
- Not many tests can do this
15
Q
Wilcoxon Test
A
- Subject design: repeated measures
-
Description: The value of the differences between the 2 conditions (e.g. Before vs After) for each person is ranked
- Small differences have low (small numbers) ranks
- Sum ranks of those scoring MORE in 2nd condition, and sum those that score LESS
- The smaller of the 2 summed values is “T”
- Compared against a critical value
- T should be equal or smaller to be significant
17
Q
Example
A
18
Q
Critical Values- Wilcoxon
A
- 3.5 is greater than 2 therefore there is no significant difference
- T must be equal to or less than the critical value in the wilcoxon table for there to be a significant difference
