Public Health Sciences - First Aid

Question 1

Observational Studies:

• frequency of disease and frequency of risk-related factors are assessed in the present
• “What is happening?”
• disease prevalence
• can show risk factor association with disease, but does not establish causality

Answer 1

Cross-Sectional Study

Question 2

Observational Studies:

• compares a group of people with disease to a group without disease.
• looks to see if odds of prior exposure or risk factor differs by disease state
• “What happened?”
• Odds Ratio (OR)

Answer 2

Case-Control Study

Question 3

Observational Studies:

• compares a group with a given exposure or risk factor to a group without such exposure
• looks to see if exposure or risk factor is associated with later development of disease
• Prospective—“Who will develop disease?”
• Retrospective—“Who developed the disease [exposed vs. nonexposed]?”
• Relative Risk (RR)

Answer 3

Cohort Study

Question 4

Observational Studies:

• compares the frequency with which both monozygotic twins vs. both dizygotic twins develop the same disease
• measures heritability and influence of environmental factors (“nature vs. nurture”)

Answer 4

Twin Concordance Study

Question 5

Observational Studies:

• compares siblings raised by biological vs. adoptive parents
• measures heritability and influence of environmental factors

Answer 5

Adoption Study

Question 6

A _____ is an experimental study involving humans. Compares therapeutic benefits of 2 or more treatments, or of treatment and placebo.

Answer 6

Clinical Trial

Question 7

Study quality improves when the study is randomized, controlled, and _____ (ie. neither patient nor doctor knows whether the patient is in the treatment or control group).

Answer 7

Double-Blinded

Question 8

_____ refers to the additional blinding of the researchers analyzing the data.

Answer 8

Triple-Blind

Question 9

Four Phases of Clinical Trials

Answer 9

“Does the drug SWIM?

1. Is it Safe?
2. Does it Work?
3. Any Improvement?
4. Can it stay in the Market?

Question 10

Phases of Clinical Trials:

• small number of healthy volunteers or patients with disease of interest
• “Is it safe?”
• assesses safety, toxicity, pharmacokinetics, and pharmacodynamics

Answer 10

Phase I

Question 11

Phases of Clinical Trials:

• moderate number of patients with disease of interest
• “Does it work?”
• assesses treatment efficacy, optimal dosing, and adverse effects

Answer 11

Phase II

Question 12

Phases of Clinical Trials:

• large number of patients randomly assigned either to the treatment under investigation or to the best available treatment (or placebo)
• “Is it as good or better?”
• compares the new treatment to the current standard of care

Answer 12

Phase III

Question 13

Phases of Clinical Trials:

• postmarketing surveillance of patients after treatment is approved
• “Can it stay?”
• detects rare or long-term adverse effects
• can result in treatment being withdrawn from market

Answer 13

Phase IV

Question 14

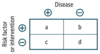
Evaluation of Diagnostic Tests

Answer 14

• Uses 2 × 2 table comparing test results with the actual presence of disease.
• Sensitivity and specificity are fixed properties of a test. PPV and NPV vary depending on disease prevalence in population being tested.

Question 15

Evaluation of Diagnostic Tests:

• proportion of all people with disease who test positive, or the probability that when the disease is present, the test is positive
• value approaching 100% is desirable for ruling out disease and indicates a low false-negative rate
• used for screening in diseases with low prevalence

Answer 15

Sensitivity (True-Positive Rate)

• Sn = TP / (TP + FN)
• Sn = 1 – FN rate
• SN-N-OUT = highly SeNsitive test, when Negative, rules OUT disease
• if sensitivity is 100%, then FN is zero
• all negatives must be TNs

Question 16

Evaluation of Diagnostic Tests:

• proportion of all people without disease who test negative, or the probability that when the disease is absent, the test is negative
• value approaching 100% is desirable for ruling in disease and indicates a low false-positive rate
• used for confirmation after a positive screening test

Answer 16

Specificity (True-Negative Rate)

• Sp = TN / (TN + FP)
• Sp = 1 – FP rate
• SP-P-IN = highly SPecific test, when Positive, rules IN disease
• if specificity is 100%, then FP is zero
• all positives must be TPs

Question 17

Evaluation of Diagnostic Tests:

probability that a person who has a positive test result actually has the disease

Answer 17

Positive Predictive Value

• PPV = TP / (TP + FP)
• PPV varies directly with pretest probability (baseline risk, such as prevalence of disease)
• high pretest probability → high PPV

Question 18

Evaluation of Diagnostic Tests:

probability that a person with a negative test result actually does not have the disease

Answer 18

Negative Predictive Value

• NPV = TN / (TN + FN)
• NPV varies inversely with prevalence or pretest probability

Question 19

Possible Cutoff Values

Answer 19

Question 20

_____ is the likelihood that a given test result would be expected in a patient with the target disorder compared to the likelihood that the same result would be expected in a patient without the target disorder.

Answer 20

Likelihood Ratio

• LR+ > 10 and/or LR– < 0.1 indicate a very useful diagnostic test
• LRs can be multiplied with pretest odds of disease to estimate posttest odds

Question 21

Quantifying Risk

Answer 21

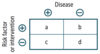
Definitions and formulas are based on the classic 2 × 2 or contingency table.

Question 22

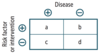
Quantifying Risk:

• typically used in case-control studies
• depicts the odds of a certain exposure given an event (eg. disease; a/c) vs. the odds of exposure in the absence of that event (eg. no disease; b/d)

Answer 22

Odds Ratio

Question 23

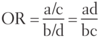
Quantifying Risk:

• typically used in cohort studies
• risk of developing disease in the exposed group divided by risk in the unexposed group (eg. if 5/10 people exposed to radiation get cancer, and 1/10 people not exposed to radiation get cancer, the _____ is 5, indicating a 5 times greater risk of cancer in the exposed than unexposed)
• for rare diseases (low prevalence), OR approximates _____.

Answer 23

Relative Risk

• RR = 1 → no association between exposure and disease
• RR > 1 → exposure associated with ↑ disease occurrence
• RR < 1 → exposure associated with ↓ disease occurrence

Question 24

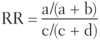
Quantifying Risk:

the difference in risk between exposed and unexposed groups (eg. if risk of lung cancer in smokers is 21% and risk in nonsmokers is 1%, then the attributable risk is 20%)

Answer 24

Attributable Risk

Question 25

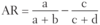
Quantifying Risk: the proportion of risk reduction attributable to the intervention as compared to a control (eg. if 2% of patients who receive a flu shot develop the flu, while 8% of unvaccinated patients develop the flu, then RR = 2/8 = 0.25, and _____ = 0.75)

Answer 25

Relative Risk Reduction * RRR = 1 − RR

Question 26

Quantifying Risk: the difference in risk (not the proportion) attributable to the intervention as compared to a control (eg. if 8% of people who receive a placebo vaccine develop the flu vs. 2% of people who receive a flu vaccine, then \_\_\_\_\_ = 8% − 2% = 6% = .06).

Answer 26

Absolute Risk Reduction

Question 27

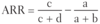
Quantifying Risk: * number of patients who need to be treated for 1 patient to benefit * lower number = better treatment

Answer 27

Number Needed to Treat * NNT = 1/ARR

Question 28

Quantifying Risk: * number of patients who need to be exposed to a risk factor for 1 patient to be harmed * higher number = safer exposure

Answer 28

Number Needed to Harm * NNH = 1/AR

Question 29

Incidence vs. Prevalence

Answer 29

* **Incidence** looks at new cases (**incidents**) * Prev**al**ence looks at **all** current cases * prevalence ∼ pretest probability * ↑ prevalence → ↑ PPV and ↓ NPV

Question 30

\_\_\_\_\_ is the consistency and reproducibility of a test. It is the absence of random variation in a test.

Answer 30

Precision (Reliability) * random error ↓ precision in a test * ↑ precision → ↓ standard deviation * ↑ precision → ↑ statistical power (1 − β)

Question 31

\_\_\_\_\_ is the trueness of test measurements. It is the absence of systematic error or bias in a test.

Answer 31

Accuracy (Validity) * systematic error ↓ accuracy in a test

Question 32

Bias and Study Errors: Recruiting Participants

Answer 32

Selection Bias

Question 33

Bias and Study Errors: * nonrandom sampling or treatment allocation of subjects such that study population is not representative of target population * most commonly a sampling bias

Answer 33

Selection Bias

Question 34

Bias and Study Errors: * selection bias * study population selected from hospital is less healthy than general population

Answer 34

Berkson Bias

Question 35

Bias and Study Errors: * selection bias * participating subjects differ from non-respondents in meaningful ways

Answer 35

Non-Response Bias

Question 36

Bias and Study Errors: Selection Bias can be reduced by \_\_\_\_\_.

Answer 36

* randomization * choice of the right comparison/reference group

Question 37

Bias and Study Errors: Performing Study

Answer 37

* Recall Bias * Measurement Bias * Procedure Bias * Observer-Expectancy Bias

Question 38

Bias and Study Errors: * awareness of disorder alters recall by subjects * common in retrospective studies * patients with disease recall exposure after learning of similar cases

Answer 38

Recall Bias

Question 39

Bias and Study Errors: Recall Bias can be reduced by \_\_\_\_\_.

Answer 39

decreasing the time from exposure to follow-up

Question 40

Bias and Study Errors: * information is gathered in a systemically distorted manner * association between HTN and MI not observed when using faulty automatic sphygmomanometer

Answer 40

Measurement Bias

Question 41

Bias and Study Errors: * measurement bias * participants change behavior upon awareness of being observed

Answer 41

Hawthorne Effect

Question 42

Bias and Study Errors: Measurement Bias can be reduced by \_\_\_\_\_.

Answer 42

* using objective, standardized, and previously tested methods of data collection that are planned ahead of time * using a placebo group

Question 43

Bias and Study Errors: * subjects in different groups are not treated the same * patients in treatment group spend more time in highly specialized hospital units

Answer 43

Procedure Bias

Question 44

Bias and Study Errors: Procedure Bias can be reduced by \_\_\_\_\_.

Answer 44

blinding and using of placebo to reduce influence of participants and researchers on procedures and interpretation of outcomes as neither are aware of group allocation

Question 45

Bias and Study Errors: * researcher’s belief in the efficacy of a treatment changes the outcome of that treatment (aka. Pygmalion effect) * an observer expecting treatment group to show signs of recovery is more likely to document positive outcomes

Answer 45

Observer-Expectancy Bias

Question 46

Bias and Study Errors: Observer-Expectancy Bias can be reduced by \_\_\_\_\_.

Answer 46

blinding and using of placebo to reduce influence of participants and researchers on procedures and interpretation of outcomes as neither are aware of group allocation

Question 47

Bias and Study Errors: Interpreting Results

Answer 47

* Confounding Bias * Lead-Time Bias * Length-Time Bias

Question 48

Bias and Study Errors: * when a factor is related to both the exposure and outcome, but not on the causal pathway, it distorts or confuses effect of exposure on outcome * contrast with effect modification * pulmonary disease is more common in coal workers than the general population; however, people who work in coal mines also smoke more frequently than the general population

Answer 48

Confounding Bias

Question 49

Bias and Study Errors: Confounding Bias can be reduced by \_\_\_\_\_.

Answer 49

* repeating studies * using crossover studies (subjects act as their own controls) * matching (patients with similar characteristics in both treatment and control groups)

Question 50

Bias and Study Errors: * early detection is confused with ↑ survival * early detection makes it seem like survival has increased, but the disease’s natural history has not changed

Answer 50

Lead-Time Bias

Question 51

Bias and Study Errors: Lead-Time Bias can be reduced by \_\_\_\_\_.

Answer 51

measuring “back-end” survival (adjust survival according to the severity of disease at the time of diagnosis)

Question 52

Bias and Study Errors: * screening test detects diseases with long latency period, while those with shorter latency period become symptomatic earlier * a slowly progressive cancer is more likely detected by a screening test than a rapidly progressive cancer

Answer 52

Length-Time Bias

Question 53

Bias and Study Errors: Length-Time Bias can be reduced by \_\_\_\_\_.

Answer 53

a randomized controlled trial assigning subjects to the screening program or to no screening

Question 54

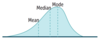
Statistical Distribution: Measures of Central Tendency

Answer 54

* Mean * Median * Mode

Question 55

Measures of Central Tendency: * (sum of values)/(total number of values) * most affected by outliers (extreme values)

Answer 55

Mean

Question 56

Measures of Central Tendency: * middle value of a list of data sorted from least to greatest * if there is an even number of values, it will be the average of the middle two values

Answer 56

Median

Question 57

Measures of Central Tendency: * most common value * least affected by outliers

Answer 57

Mode

Question 58

Statistical Distribution: Measures of Dispersion

Answer 58

* Standard Deviation * Standard Error

Question 59

Measures of Dispersion: how much variability exists in a set of values, around the mean of these values

Answer 59

Standard Deviation * σ = SD * Variance = (SD)2

Question 60

Measures of Dispersion: an estimate of how much variability exists in a (theoretical) set of sample means around the true population mean

Answer 60

Standard Error * σ = SD * n = sample size * SE = σ/√n * SE ↓ as n ↑

Question 61

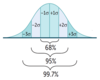
Normal Distribution

Answer 61

* Gaussian, also called bell-shaped. * Mean = Median = Mode

Question 62

Non-Normal Distributions: * suggests two different populations * metabolic polymorphism such as fast vs. slow acetylators * age at onset of Hodgkin lymphoma * suicide rate by age

Answer 62

Bimodal

Question 63

Non-Normal Distributions: * Mean \> Median \> Mode * asymmetry with longer tail on right

Answer 63

Positive Skew

Question 64

Non-Normal Distributions: * Mean \< Median \< Mode * asymmetry with longer tail on left

Answer 64

Negative Skew

Question 65

Statistical Hypotheses: * hypothesis of no difference or relationship * there is no association between the disease and the risk factor in the population

Answer 65

Null (H₀)

Question 66

Statistical Hypotheses: * hypothesis of some difference or relationship * there is some association between the disease and the risk factor in the population

Answer 66

Alternative (H₁)

Question 67

Outcomes of Statistical Hypothesis Testing: * stating that there is an effect or difference when one exists (null hypothesis rejected in favor of alternative hypothesis) * stating that there is no effect or difference when none exists (null hypothesis not rejected)

Answer 67

Correct Result

Question 68

Outcomes of Statistical Hypothesis Testing: * incorrect result * stating that there is an effect or difference when none exists (null hypothesis incorrectly rejected in favor of alternative hypothesis). * p is judged against a preset __ level of significance (usually 0.05) * if p \< 0.05, then there is less than a 5% chance that the data will show something that is not really there

Answer 68

Type I Error (α) * false-positive error * α is the probability of making a type I error * **α** = you **a**ccused an innocent man. * You can never “prove” the alternate hypothesis, but you can reject the null hypothesis as being very unlikely.

Question 69

Outcomes of Statistical Hypothesis Testing: * stating that there is not an effect or difference when one exists (null hypothesis is not rejected when it is in fact false). * __ is related to statistical power (1 – \_\_), which is the probability of rejecting the null hypothesis when it is false

Answer 69

Type II Error (β) * false-negative error * β is the probability of making a type II error * **β** = you **b**lindly let the guilty man go free * If you ↑ sample size, you ↑ power; there is power in numbers.

Question 70

↑ power and ↓ β by \_\_\_\_\_.

Answer 70

* ↑ sample size * ↑ expected effect size * ↑ precision of measurement

Question 71

\_\_\_\_\_ is the range of values within which the true mean of the population is expected to fall, with a specified probability.

Answer 71

Confidence Interval * CI for sample mean = x¯ ± Z(SE) * The 95% CI (corresponding to α = .05) is often used. * 95% CI → Z = 1.96 * 99% CI → Z = 2.58

Question 72

Confidence Interval: If the 95% CI for a mean difference between 2 variables includes 0, then \_\_\_\_\_.

Answer 72

* there is no significant difference * H₀ is not rejected

Question 73

Confidence Interval: If the 95% CI for odds ratio or relative risk includes 1, \_\_\_\_\_.

Answer 73

H₀ is not rejected

Question 74

Confidence Interval: If the CIs between 2 groups do not overlap, \_\_\_\_\_.

Answer 74

statistically significant difference exists

Question 75

Confidence Interval: If the CIs between 2 groups overlap, \_\_\_\_\_.

Answer 75

usually no significant difference exists

Question 76

\_\_\_\_\_ is a method of statistical analysis that pools summary data (eg. means, RRs) from multiple studies for a more precise estimate of the size of an effect. It also estimates heterogeneity of effect sizes between studies. It improves strength of evidence and generalizability of study findings. It is limited by quality of individual studies and bias in study selection.

Answer 76

Meta-Analysis

Question 77

Statistical Tests: * checks differences between means of 2 groups * comparing the mean blood pressure between men and women

Answer 77

T-Test **T**ea is meant for **2**.

Question 78

Statistical Tests: * checks differences between means of 3 or more groups * comparing the mean blood pressure between members of 3 different ethnic groups

Answer 78

ANOVA **3** words: **AN**alysis **O**f **VA**riance

Question 79

Statistical Tests: * checks differences between 2 or more percentages or proportions of categorical outcomes (not mean values) * comparing the percentage of members of 3 different ethnic groups who have essential hypertension

Answer 79

Chi-square (χ²) **Chi**-tegorical

Question 80

Pearson Correlation Coefficient

Answer 80

* r is always between −1 and +1 * The closer the absolute value of r is to 1, the stronger the linear correlation between the 2 variables. * Positive r value → positive correlation (as one variable ↑, the other variable ↑). * Negative r value → negative correlation (as one variable ↑, the other variable ↓). * Coefficient of determination = r² (amount of variance in one variable that can be explained by variance in another variable).

Question 81

Core Ethical Principles

Answer 81

* Autonomy * Beneficence * Nonmaleficence * Justice

Question 82

Core Ethical Principles: * respect patients as individuals (truth-telling, confidentiality) * create conditions necessary for autonomous choice (informed consent) * honor their preference in accepting or not accepting medical care

Answer 82

Autonomy

Question 83

Core Ethical Principles: * Physicians have a special ethical (fiduciary) duty to act in the patient’s best interest. * may conflict with autonomy (an informed patient has the right to decide) or what is best for society (eg. mandatory TB treatment) * Traditionally, patient interest supersedes.

Answer 83

Beneficence

Question 84

Core Ethical Principles: * “Do no harm.” * must be balanced against beneficence * If the benefits outweigh the risks, a patient may make an informed decision to proceed (most surgeries and medications fall into this category).

Answer 84

Nonmaleficence

Question 85

Core Ethical Principles: * treat persons fairly and equitably * does not always imply equally (eg. triage)

Answer 85

Justice

Question 86

Informed consent is a process (not just a document/signature) that requires \_\_\_\_\_.

Answer 86

* _Disclosure_: discussion of pertinent information * _Understanding_: ability to comprehend * _Capacity_: ability to reason and make one’s own decisions (distinct from competence, a legal determination) * _Voluntariness_: freedom from coercion and manipulation Patients must have an intelligent understanding of their diagnosis and the risks/benefits of proposed treatment and alternative options, including no treatment. Patient must be informed that he or she can revoke written consent at any time, even orally.

Question 87

Exceptions to Informed Consent

Answer 87

**WIPE** it away: * _**W**aiver_—patient explicitly waives the right of informed consent * _Legally **I**ncompetent_—patient lacks decision-making capacity (obtain consent from legal surrogate) * _Therapeutic **P**rivilege_—withholding information when disclosure would severely harm the patient or undermine informed decision-making capacity * _**E**mergency Situation_—implied consent may apply

Question 88

Consent for Minors

Answer 88

* A minor is generally any person \< 18 years old. * Parental consent laws in relation to healthcare vary by state. * In general, parental consent should be obtained, but exceptions exist for emergency treatment (eg. blood transfusions) or if minor is legally emancipated (eg. married, self supporting, or in the military). * Physicians should always encourage healthy minor-guardian communication. * Physician should seek a minor’s assent even if their consent is not required.

Question 89

Situations in which Parental Consent is Inessential

Answer 89

* **Sex** (contraception, STIs, pregnancy) * **Drugs** (substance abuse) * **Rock and Roll** (emergency/trauma)

Question 90

Decision-Making Capacity

Answer 90

* Physician must determine whether the patient is psychologically and legally capable of making a particular healthcare decision. * Note that decisions made with capacity cannot be revoked simply if the patient later loses capacity. * Capacity is determined by a physician for a specific healthcare-related decision (eg. to refuse medical care). * Competency is determined by a judge and usually refers to more global categories of decision making (eg. legally unable to make any healthcare-related decision).

Question 91

Decision-Making Capacity Components

Answer 91

**GIEMSA**: * Decision is consistent with patient’s values and **G**oals * Patient is **I**nformed (knows and understands) * Patient **E**xpresses a choice * Decision is not a result of altered **M**ental status (eg. delirium, psychosis, intoxication) or **M**ood disorder * Decision remains **S**table over time * Patient is ≥ 18 years of **A**ge or otherwise legally emancipated

Question 92

\_\_\_\_\_ are instructions given by a patient in anticipation of the need for a medical decision. Details vary per state law.

Answer 92

Advance Directives

Question 93

Advance Directives: * incapacitated patient’s prior oral statements commonly used as guide * problems arise from variance in interpretation * if patient was informed, directive was specific, patient made a choice, and decision was repeated over time to multiple people, then the oral directive is more valid

Answer 93

Oral Advance Directive

Question 94

Advance Directives: * specifies specific healthcare interventions that a patient anticipates he or she would accept or reject during treatment for a critical or life-threatening illness * living will

Answer 94

Written Advance Directive

Question 95

Advance Directives: * patient designates an agent to make medical decisions in the event that he/she loses decision-making capacity * patient may also specify decisions in clinical situations * can be revoked by patient if decision-making capacity is intact * more flexible than a living wil

Answer 95

Medical Power of Attorney

Question 96

Advance Directives: * prohibits cardiopulmonary resuscitation (CPR) * other resuscitative measures that may follow (eg. intubation) are also typically avoided

Answer 96

Do Not Resuscitate Order (DNR)

Question 97

Surrogate Decision-Maker

Answer 97

* If a patient loses decision-making capacity and has not prepared an advance directive, individuals (surrogates) who know the patient must determine what the patient would have done. * Priority of Surrogates: **spouse** → adult **Chi**ldren → **P**arents → **S**iblings → other relatives (the **spouse ChiPS** in)

Question 98

Ethical Situations: Patient is not adherent.

Answer 98

* Attempt to identify the reason for nonadherence and determine his/her willingness to change. * Do not coerce the patient into adhering and do not refer him/her to another physician.

Question 99

Ethical Situations: Patient desires an unnecessary procedure.

Answer 99

* Attempt to understand why the patient wants the procedure and address underlying concerns. * Do not refuse to see the patient and do not refer him/her to another physician. * Avoid performing unnecessary procedures.

Question 100

Ethical Situations: Patient has difficulty taking medications.

Answer 100

* Provide written instructions. * Attempt to simplify treatment regimens. * Use teach-back method (ask patient to repeat regimen back to physician) to ensure comprehension.

Question 101

Ethical Situations: Family members ask for information about the patient’s prognosis.

Answer 101

Avoid discussing issues with relatives without the patient’s permission.

Question 102

Ethical Situations: A patient’s family member asks you not to disclose the results of a test if the prognosis is poor because the patient will be “unable to handle it.”

Answer 102

* Attempt to identify why the family member believes such information would be detrimental to the patient’s condition. * Explain that as long as the patient has decision-making capacity and does not indicate otherwise, communication of information concerning his/her care will not be withheld. * However, if you believe the patient might seriously harm himself or others if informed, then you may invoke therapeutic privilege and withhold the information.

Question 103

Ethical Situations: A 17-year-old girl is pregnant and requests an abortion.

Answer 103

* Many states require parental notification or consent for minors for an abortion. * Unless there are specific medical risks associated with pregnancy, a physician should not sway the patient’s decision for, or against, an elective abortion (regardless of maternal age or fetal condition).

Question 104

Ethical Situations: A 15-year-old girl is pregnant and wants to keep the child. Her parents want you to tell her to give the child up for adoption.

Answer 104

* The patient retains the right to make decisions regarding her child, even if her parents disagree. * Provide information to the teenager about the practical issues of caring for a baby. * Discuss the options, if requested. * Encourage discussion between the teenager and her parents to reach the best decision.

Question 105

Ethical Situations: A terminally ill patient requests physician assistance in ending his/her own life.

Answer 105

* In the overwhelming majority of states, refuse involvement in any form of physician-assisted suicide. * Physicians may, however, prescribe medically appropriate analgesics that coincidentally shorten the patient’s life.

Question 106

Ethical Situations: Patient is suicidal.

Answer 106

* Assess the seriousness of the threat. * If it is serious, suggest that the patient remain in the hospital voluntarily; patient can be hospitalized involuntarily if he/she refuses.

Question 107

Ethical Situations: Patient states that he/she finds you attractive.

Answer 107

* Ask direct, closed-ended questions and use a chaperone if necessary. * Romantic relationships with patients are never appropriate. * It may be necessary to transition care to another physician.

Question 108

Ethical Situations: A woman who had a mastectomy says she now feels “ugly.”

Answer 108

* Find out why the patient feels this way. * Do not offer falsely reassuring statements (eg. “You still look good”).

Question 109

Ethical Situations: Patient is angry about the long time he/she spent in the waiting room.

Answer 109

* Acknowledge the patient’s anger, but do not take a patient’s anger personally. * Apologize for any inconvenience. * Stay away from efforts to explain the delay.

Question 110

Ethical Situations: Patient is upset with the way he/she was treated by another doctor.

Answer 110

* Suggest that the patient speak directly to that physician regarding his/her concerns. * If the problem is with a member of the office staff, tell the patient you will speak to that person.

Question 111

Ethical Situations: An invasive test is performed on the wrong patient.

Answer 111

Regardless of the outcome, a physician is ethically obligated to inform a patient that a mistake has been made.

Question 112

Ethical Situations: A patient requires a treatment not covered by his/her insurance.

Answer 112

* Never limit or deny care because of the expense in time or money. * Discuss all treatment options with patients, even if some are not covered by their insurance companies.

Question 113

Ethical Situations: A 7-year-old boy loses a sister to cancer and now feels responsible.

Answer 113

* At ages 5–7, children begin to understand that death is permanent, that all life functions end completely at death, and that everything that is alive eventually dies. * Provide a direct, concrete description of his sister’s death. * Avoid clichés and euphemisms. * Reassure the boy that he is not responsible. * Identify and normalize fears and feelings. * Encourage play and healthy coping behaviors (eg. remembering her in his own way).

Question 114

Ethical Situations: Patient is victim of intimate partner violence.

Answer 114

* Ask if patient is safe and has an emergency plan. * Do not necessarily pressure patient to leave his or her partner, or disclose the incident to the authorities (unless required by state law).

Question 115

Ethical Situations: Patient wants to try alternative or holistic medicine.

Answer 115

Find out why and allow patient to do so as long as there are no contraindications, medication interactions, or adverse effects to the new treatment.

Question 116

Ethical Situations: Physician colleague presents to work impaired.

Answer 116

* If impaired or incompetent, colleague is a threat to patient safety. * Report the situation to local supervisory personnel. * Should the organization fail to take action, alert the state licensing board.

Question 117

Ethical Situations: Patient is officially determined to suffer brain death. Patient’s family insists on maintaining life support indefinitely because patient is still moving when touched.

Answer 117

* Gently explain to family that there is no chance of recovery, and that brain death is equivalent to death. * Movement is due to spinal arc reflex and is not voluntary. * Bring case to appropriate ethics board regarding futility of care and withdrawal of life support.

Question 118

Ethical Situations: A pharmaceutical company offers you a sponsorship in exchange for advertising its new drug.

Answer 118

* Reject this offer. * Generally, decline gifts and sponsorships to avoid any appearance of conflict of interest. * The AMA Code of Ethics does make exceptions for gifts directly benefitting patients; gifts of minimal value; special funding for medical education of students, residents, fellows; grants whose recipients are chosen by independent institutional criteria; and funds that are distributed without attribution to sponsors.

Question 119

Ethical Situations: An adult refuses care because it is against his/her religious beliefs.

Answer 119

* Work with the patient by either explaining the treatment or pursuing alternative treatments. * However, a physician should never force a competent adult to receive care if it is contrary to the patient’s religious beliefs.

Question 120

Ethical Situations: Mother and 15-year-old daughter are unresponsive following a car accident and are bleeding internally. Father says do not transfuse because they are Jehovah’s Witnesses.

Answer 120

* Transfuse daughter, but do not transfuse mother. * Emergent care can be refused by the healthcare proxy for an adult, particularly when patient preferences are known or reasonably inferred, but not for a minor based solely on faith.

Question 121

Ethical Situations: A 2-year-old girl presents with injuries inconsistent with parental story.

Answer 121

* Contact child protective services and ensure child is in a safe location. * Physicians are required by law to report any reasonable suspicion of child abuse or endangerment.

Question 122

Confidentiality

Answer 122

* Confidentiality respects patient privacy and autonomy. * If the patient is incapacitated or the situation is emergent, disclosing information to family and friends should be guided by professional judgment of patient’s best interest. * The patient may voluntarily waive the right to confidentiality (eg. insurance company request).

Question 123

General Principles for Exceptions to Confidentiality

Answer 123

* potential physical harm to others is serious and imminent * likelihood of harm to self is great * no alternative means exist to warn or to protect those at risk * physicians can take steps to prevent harm

Question 124

Exceptions to Patient Confidentiality

Answer 124

“The physician’s good judgment **SAVED** the day.” * **S**uicidal/homicidal patients * **A**buse (children, elderly, and/or prisoners) * **D**uty to protect—state-specific laws that sometimes allow physician to inform or somehow protect potential **V**ictim from harm * **E**pileptic patients and other impaired automobile drivers * Reportable **D**iseases (eg. STIs, hepatitis, food poisoning)—physicians may have a duty to warn public officials, who will then notify people at risk; dangerous communicable diseases, such as TB or Ebola, may require involuntary treatment

Question 125

Children should ride in rear-facing car seats until they are \_\_\_\_\_.

Answer 125

2 years old

Question 126

Children should ride in car seats with a harness until they are \_\_\_\_\_.

Answer 126

4 years old

Question 127

Older children should use a booster seat until they are _____ or until the seat belt fits properly.

Answer 127

8 years old

Question 128

Children _____ should not ride in a seat with a front-facing airbag.

Answer 128

\< 12 years old

Question 129

Sexual Changes in the Elderly

Answer 129

* Men—slower erection/ejaculation, longer refractory period * Women—vaginal shortening, thinning, and dryness

Question 130

Sleep Pattern Changes in the Elderly

Answer 130

* ↓ REM and slow-wave sleep * ↑ sleep onset latency * ↑ early awakenings

Question 131

Changes in the Elderly:

Answer 131

* ↑ suicide rate * ↓ vision and hearing * ↓ immune response * ↓ renal, pulmonary, and GI function * ↓ muscle mass * ↑ fat * intelligence does not decrease

Question 132

Disease Prevention: * prevent disease before it occurs * HPV vaccination

Answer 132

Primary Disease Prevention

Question 133

Disease Prevention: * screen early for and manage existing but asymptomatic disease * Pap smear for cervical cancer

Answer 133

Secondary Disease Prevention

Question 134

Disease Prevention: * treatment to reduce complications from disease that is ongoing or has long-term effects * chemotherapy

Answer 134

Tertiary Disease Prevention

Question 135

Disease Prevention: * identifying patients at risk of unnecessary treatment, protecting from the harm of new interventions * electronic sharing of patient records to avoid duplicating recent imaging studies

Answer 135

Quaternary Disease Prevention

Question 136

Major Medical Insurance Plans: * restricted to limited panel (except emergencies) * no referral required

Answer 136

Exclusive Provider Organization

Question 137

Major Medical Insurance Plans: * restricted to limited panel (except emergencies) * denied for any service that does not meet established, evidence-based guidelines * requires referral from primary care provider

Answer 137

Health Maintenance Organization

Question 138

Major Medical Insurance Plans: * patient can see providers outside network * higher copays and deductibles for out-ofnetwork services * requires referral from primary care provider

Answer 138

Point of Service

Question 139

Major Medical Insurance Plans: * patient can see providers outside network * higher copays and deductibles for all services * no referral required

Answer 139

Preferred Provider Organization

Question 140

\_\_\_\_\_ are federal social healthcare programs that originated from amendments to the Social Security Act.

Answer 140

* Medicare * Medicaid

Question 141

\_\_\_\_\_ is available to patients ≥ 65 years old, \< 65 with certain disabilities, and those with end-stage renal disease.

Answer 141

Medicare Medicar**E** is for the **E**lderly.

Question 142

\_\_\_\_\_ is joint federal and state health assistance for people with limited income and/or resources.

Answer 142

Medicaid Medicai**D** is for the **D**estitute.

Question 143

4 Parts of Medicare:

Answer 143

* Part **A**: Hospit**A**l insurance, home hospice care * Part **B**: **B**asic medical bills (eg. doctor’s fees, diagnostic testing) * Part **C**: (parts A + B = **C**ombo) delivered by approved private companies * Part **D**: Prescription **D**rugs

Question 144

\_\_\_\_\_ is medical care focused on providing comfort and palliation instead of definitive cure. Available to patients on Medicare or Medicaid and in most private insurance plans whose life expectancy is \< 6 months.

Answer 144

Hospice Care

Question 145

During end-of-life care, priority is given to improving the patient’s comfort and relieving pain (often includes opioid, sedative, or anxiolytic medications). Facilitating comfort is prioritized over potential side effects (eg. respiratory depression). This prioritization of positive effects over negative effects is known as the \_\_\_\_\_.

Answer 145

Principle of Double Effect

Question 146

Common Causes of Death (US): \< 1 y.o.

Answer 146

1. Congenital Malformations 2. Preterm Birth 3. SIDS

Question 147

Common Causes of Death (US): 1-14 y.o.

Answer 147

1. Unintentional Injury 2. Cancer 3. Congenital Malformations

Question 148

Common Causes of Death (US): 15-25 y.o.

Answer 148

1. Unintentional Injury 2. Suicide 3. Homicide

Question 149

Common Causes of Death (US): 35-44 y.o.

Answer 149

1. Unintentional Injury 2. Cancer 3. Heart Disease

Question 150

Common Causes of Death (US): 45-64 y.o.

Answer 150

1. Cancer 2. Heart Disease 3. Unintentional Injury

Question 151

Common Causes of Death (US): 65+ y.o.

Answer 151

1. Heart Disease 2. Cancer 3. Chronic Respiratory Disease

Question 152

Hospitalized Conditions with Frequent Readmissions: Medicare \*defined as readmission for any reason within 30 days of discharge from original admission

Answer 152

1. Congestive HF 2. Septicemia 3. Pneumonia

Question 153

Hospitalized Conditions with Frequent Readmissions: Medicaid \*defined as readmission for any reason within 30 days of discharge from original admission

Answer 153

1. Mood Disorders 2. Schizophrenia/Psychotic Disorders 3. Diabetes Mellitus with Complications

Question 154

Hospitalized Conditions with Frequent Readmissions: Private Insurance \*defined as readmission for any reason within 30 days of discharge from original admission

Answer 154

1. Maintenance of Chemotherapy or Radiotherapy 2. Mood Disorders 3. Complications of Surgical Procedures or Medical Care

Question 155

Hospitalized Conditions with Frequent Readmissions: Uninsured \*defined as readmission for any reason within 30 days of discharge from original admission

Answer 155

1. Mood Disorders 2. Alcohol-Related Disorders 3. Diabetes Mellitus with Complications

Question 156

\_\_\_\_\_ is an organizational environment in which everyone can freely bring up safety concerns without fear of censure. Facilitates error identification. Event reporting systems collect data on errors for internal and external monitoring.

Answer 156

Safety Culture

Question 157

Human Factors Design

Answer 157

* Forcing functions (those that prevent undesirable actions [eg. connecting feeding syringe to IV tubing]) are the most effective. * Standardization improves process reliability (eg. clinical pathways, guidelines, checklists). * Simplification reduces wasteful activities (eg. consolidating electronic medical records). * Deficient designs hinder workflow and lead to staff workarounds that bypass safety features (eg. patient ID barcodes affixed to computers due to unreadable wristbands).

Question 158

PDSA Cycle

Answer 158

Process improvement model to test changes in real clinical setting. Impact on patients: * **P**lan—define problem and solution * **D**o—test new process * **S**tudy—measure and analyze data * **A**ct—integrate new process into regular workflow

Question 159

Quality Measurements: * physical equipment, resources, and facilities * number of diabetes educators

Answer 159

Structural

Question 160

Quality Measurements: * performance of system as planned * percentage of diabetic patients whose HbA_1c was measured in the past 6 months

Answer 160

Process

Question 161

Quality Measurements: * impact on patients * average HbA_1c of patients with diabetes

Answer 161

Outcome

Question 162

Quality Measurements: * impact on other systems/outcomes * incidence of hypoglycemia among patients who tried an intervention to lower HbA_1c

Answer 162

Balancing

Question 163

Swiss Cheese Model

Answer 163

* Focuses on systems and conditions rather than an individual’s error. * The risk of a threat becoming a reality is mitigated by differing layers and types of defenses. * Patient harm can occur despite multiple safeguards when “the holes in the cheese line up."

Question 164

Types of Medical Errors: * occurs at level of frontline operator (eg. wrong IV pump dose programmed) * immediate impact

Answer 164

Active Error

Question 165

Types of Medical Errors: * occurs in processes indirect from operator but impacts patient care (eg. different types of IV pumps used within same hospital) * accident waiting to happen

Answer 165

Latent Error

Question 166

Medical Error Analysis: * retrospective approach * applied after failure event to prevent recurrence * uses records and participant interviews to identify all the underlying problems (eg. process, people, environment, equipment, materials, management) that led to an error.

Answer 166

Root Cause Analysis

Question 167

Medical Error Analysis: * forward-looking approach * applied before process implementation to prevent failure occurrence * uses inductive reasoning to identify all the ways a process might fail and prioritizes them by their probability of occurrence and impact on patients

Answer 167

Failure Mode and Effects Analysis