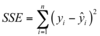Regression Analysis Flashcards
what does covariance measure?
Measures the direction of linear relationship between two (continuous) variables.
Can be positive or negative
Positive: as x increases, y tends to increase
Negative: as x increases, y tends to decrease
what does correlation coefficient measure?
strength (and direction) of the linear relationship between two variables, X and Y.
Indicates the degree to which the variation in X is related to the variation in Y.
is correlation coefficient is measured for population, it is called?
ρ
is correlation coefficient is estimated for a sample,
use r; i.e. r estimates ρ
describe results from correlation coefficient
Always between -1 and +1.
ρ =+1: perfect positive linear relationship
ρ =-1: perfect negative linear relationship
ρ =0: no linear relationship (could be a different sort of relationship between the variables)
what is covariance and correlatoin coefficient is not used with continuous variables and the variables are not normally distributed?
r will be “deflated” and underestimates ρ.
E.g. in marketing research, often use 1-5 likert scales: if rating scales have a small number of categories, data is not strictly continuous, so r will underestimate ρ
covariance and correlation coefficient are appropriate for use with
continuous variables whose distributions have the same shape (e.g. both normally distributed).
describe hypothesis test for correlation
1. Hypothesis
- Test statistic
- Decision rule
- Conclusion
H0: ρ=0 (if correlation is zero, then there is no significant linear relationship)
H1: ρ≠0
describe hypothesis test for correlation
- Hypothesis
2. Test statistic
- Decision rule
- Conclusion
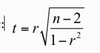
describe hypothesis test for correlation
- Hypothesis
- Test statistic
- Decision rule
4. Conclusion
in terms of whether a significant linear relationship exists.
describe hypothesis test for correlation
- Hypothesis
- Test statistic
3. Decision rule
- Conclusion
: Compare to a t-distribution with n-2 degrees of freedom
if correlation is positive, conclude that?
the greater the increase in A, the greater the increase in B
describe moderate to weak relationship of r
r is around 0.4-0.5
why do we use regression analysis?
whether and how (cts) variables are related to each other
“Whether” – does the value of one variable have any effects on the values of another?
“How” – as one variable changes, does another tend to increase or decrease?
what data is used in regression analysis?
One continuous response variable (called y - dependent variable, response variable)
One or more continuous explanatory variables (called x - independent variable, explanatory variable, predictor variable, regressor variable)
what regression does
Develops an equation which represents the relationship between the variables.
- Simple linear regression* – straight line relationship between y and x (i.e. one explanatory variable)
- Multiple linear regression* – “straight line” relationship between y and x1, x2, .., xk where we have k explanatory variables
- Non-linear regression* – relationship not a “straight line” (i.e. y is related to some function of x, e.g. log(x))
what is the objective of regression?
Interested in predicting values of Y when X takes on a specific value
model relationship through a linear model
Express random variable Y in terms of random variable X
feature of the population/ true regression line
β0 and β1 are constants to be estimated
εi is a random variable with mean = 0
Yi = β0 + β1xi + εi
response of particular retail spending to a particular value of disposable income will be in two parts – <strong>an expectation (β0+β1x) which reflects the systematic relationship</strong>, and a <strong>discrepancy (εi) which represents all the other many factors</strong> (apart from disposable income) which may affect spending.
what is the residual?
Vertical distance between observed point and fitted line is called the residual.
That is ri=yi-(b0+b1xi)
ri estimates εi, the error variable
how do you determine values of b0+b1 that best fit the data?
choose values of slope and intercept which minimise
describe the residual sum of squares method
Choose our estimates of slope and intercept to give the smallest residual sum of squares
Uses calculus to find estimates
residual sum of squares method
how do you estimate slope and intercept?
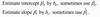
how can we show that residual sum of squares is minimised by solution?
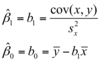
what is a residual?
ri= yi - yhat is a residual
Residuals are observed values of the errors, εi, i=1, 2, …, n.
The error sum of squares is then
The procedure gives the “line of best fit” in the sense that the SSE is minimised
what is the general rule?
can’t determine the value of y for a value of X outside our sample range of x.
how to assess the model?
If fit is poor, discard the model and fit another
Different shape, e.g. not a straight line – could mean fitting a quadratic, cubic etc; or fitting something completely different
Different predictors
assessing the model,
in our fitting, we assume
the errors have a particular distribution – that is, ε~N(0,σε²)
Normal distribution
Mean = 0
Constant variance = σε²
If σε² is small, then small spread of observations around fitted line
If σε² is large, then observations have wide spread around fitted line
Errors associated with any two y values are independent
how do you test the slope?
- Hypothesis
- Test Statistic
- Decision Rule
- Conclusion
H0: β1=constant
HA: β1≠constant
how do you test the slope?
- Hypothesis
2. Test Statistic
- Decision Rule
- Conclusion
how do you test the slope?
- Hypothesis
- Test Statistic
3. Decision Rule
4. Conclusion
Decision Rule: Compare to a t-distribution with n-2 degrees of freedom
Conclusion: In terms of whether evidence is sufficient to reject null hypothesis.
why do you have to be careful when testing intercept?
as it may be outside the prediction range, and so will not have an interpretation.
what assumptions do we have for error terms?
Assumptions:
Error terms are normally distributed
Error terms have mean of 0, constant variance
Error terms are independent – observations are indepen
what does the intercept refer to?
what happens to Y when X= 0
that is,
what happens to gross sales when no money is spent on newspaper advertising
how to determine
the strength and significance of association<!--EndFragment-->
Measured by R2 – coefficient of determination.
This measures proportion of variation in Y that is explained by variation in the independent variable X in the regression model
R2 = explained variation / total variation = (correlation coefficient)2
eg. 90.42% of the<strong> variation in </strong>annual sales is explained by variability in the size of the store
features of R2 ?
Will be between 0 and 1; a value close to 1 indicates most of the variation in y is explained by the regression equation
note.
you cannot say model fits data well unless,
Cannot say model fits data well unless assumptions about errors are met:
- Independence
- Normally distributed
- Zero mean, constant variance
(Note that zero mean of residuals is ensured by estimation process)
Examine residuals (estimates of errors) to see if assumptions are met
Graphical techniques
Assess normality from histogram, normality plot
Assess independence and variance from scatterplots of residuals vs fitted values, predictor values, order
when plotting residuals,
for preference use Standardised residuals (will have standard deviation of 1; if normally distributed, will fit a standard normal distribution).
how is normality shown?
normality shown by points being close to the line
how is normality depicted in histograms?
by the bell shape
Residuals vs fitted values
How do you indicate independence and constant variation?
Randomness indicates independence; equal spread indicates constant variation
Residuals vs order
how do you indicate independence and constant variation?
Randomness indicates independence; equal spread indicates constant variation
what does homoscedasticity appear like?
how does heteroscedasticity appear?
distinguish between homoscedasticity and heteroscedasticity
If variation is constant (residuals show constant spread around zero), called homoscedastic
If variation is non-constant (residuals show varying spread around zero), called heteroscedastic
independence of error terms
if error terms are correlated over time,
If error terms are correlated over time (or in order of collection/entry) they are said to be autocorrelated or serially correlated.
If residuals independent, should be no relationship among them
If residuals related, autocorrelation present – often happens with economic and financial data
when there is an outlier, what steps should be taken?
- Should investigate further
- Might have been a typo (should have been 30,000)
- Might not have been appropriate for sample (only 3 months old)
If all evidence indicates it is valid, should still be included (i.e. don’t just throw out data because it is unusual!)
describe influential observations
If an x-value is far away from the mean, far away from other x-observations, called “influential”
Will have a great impact on where line goes – a small change in response will result in a big change in fitted line (coefficients estimated)
what should you do when influential observations are present
Should be checked for validity, accuracy etc
when can you assume model fits data well?
High R-sq, small std error of estimate
All assumptions appear valid
what should you do when in assumption the model fits data well?
May want to use model to predict values of response for given values of predictor.
Remember: predictions should only be made for values of x within or not too far from the upper and lower observed x limits.
eg sub values for X in the equation to yield Y values
describe the two types of confidence intervals
A prediction interval for a single observation of y (an interval within which we expect single observations of the response)
- further away from the x average we are predicting, the wider our prediction interval will be.
A confidence interval for the expected value of y (an interval within which we expect to find the average response)
- CI is narrower than PI for same value of x
describe multiple regressions
two or more indepdent variables are used to predict value of dependent variable
Example: Are consumers’ perceptions of quality determined by the perceptions of prices, brand image and brand attributes
Multiple regressions
describe additive effects
Combined effects of X1 and X2 are additive – if both X1 and X2 are increased by one unit, expected change in Y would be (β1+β2).
Multiple regressions
For least squares solution, we can find solution only if
we can only find a solution if
- Number of predictors is less than number of observations
- None of the independent variables are perfectly correlated with each other
Describe strength of associtiation (R2) for multiple regression
coefficient of multiple determination
- Will go up as we add more explanatory terms to the model whether they are “important” or not
- Often we use “adjusted R2” – accounts for independent variable
- So, if comparing models with differing numbers of predictors, use “adjusted R2” to compare how much variation in response is explained by model.
multiple regression,
when significance testing what can we test?
Can test two different things
1.Significance of the overall regression
2.Significance of specific partial regression coefficients.
multiple regression,
when significance testing
1. hypothesis
- Test statistic
3. Decision Rule
4. Conclusion
H0: β1= β2= β3=…= βk=0 (no linear relationship between dependent variable and independent variables)
HA: not all slopes = 0
(at least one of the independent variables is related to sales)
Test Statistic: Found in Minitab’s “ANOVA” table
Decision Rule: Compared to an F-distribution with k, (n-k-1) degrees of freedom.
If H0 is rejected, one or more slopes are not zero. Additional tests are needed to determine which slopes are significant.
<!--StartFragment-->
Significance of specific partial regression coefficients<!--EndFragment-->
- hypothesis
- Testing statistic
3. decision rule
4. conclusion
Decision Rule: Compared to a t-distribution with (n-k-1) degrees of freedom (i.e. residual d.f. from ANOVA table) [k is the number of predictors being fitted.]
If H0 is rejected, the slope of the ith variable is significantly different from zero. That is, once the other variables are considered, the ith predictor has a significant linear relationship with the response.
<!--StartFragment-->
Significance of specific partial regression coefficients<!--EndFragment-->
1. hypothesis
- Testing statistic
- decision rule
- conclusion
H0: βi=0
HA: βi≠0
what assumptions are made for residuals?
Assumptions made:
Linearity: relationship between variables is linear
Independence of errors: errors are independent of one another
Normality: errors (εi) are normally distributed at each value of X. regression analysis robust against departure from normality assumption
**E: **homoscedasticity( equal/constant variance). Variance of the errors (εi) be constant for all values of X. variability of Y values is the same when X is a low value as when X is high
Have mean 0
what is the definition of residual
A residual (also called error term) is the difference between the observed response value Yi, and the value predicted by the regression equation Y hati
-
(Vertical distance between point and line/plane.)
Residuals
Error terms normally distributed
Error terms have mean 0, constant variance
Error terms are independent
Can be checked by looking at a histogram of the residuals - look for bell-shaped distribution.
Also normal probability plot – look for straight line.
For preference, use standardised residuals – have a std dev of 1.
Residuals
Error terms normally distributed
Error terms have mean 0, constant variance
Error terms are independent
Checked by using plots of
- residuals vs predicted values
- residuals vs independent variables.
Look for random scatter of points around zero.
If not, (esp res vs indep), may indicate linear regression is not appropriate – may need to transform data (see tutorial)
Residuals
Error terms normally distributed
Error terms have mean 0, constant variance
Error terms are independent
Check in previous plots; also in residuals vs time/order.
Look for random scatter of residuals.
what model does a polynomial model fit?
X1 = x
X2 = x2
X3 = x3
Polynomial regression
<!--StartFragment-->
Interaction term<!--EndFragment-->
This is needed if the level of X1 affects the relationship between X2 and Y.
purpose of regression analysis
develop model to predict values of a numerical variable, based on value of other variables
describe simple linear regression
single numerical indepdent variable, X is used to predict numerical dependant variable Y
the simplest relationship between two variables is known as
a linear relationship or straight-line relationship
what is the simple linear regression model and what does each symbol represent?
Yi = β0 + β1Xi + εi
β0 = Y intercept for population (mean value of Y when X= 0)
β1 = slope for population (change in Y per unit change in X)
εi = random error in Y for each observation i (vertical distance of actual value of Yi above or below the expected value of Yi on the line)
Yi = dependent variable (response variable) for observation i
Xi = independent variable (predictor/explanatory variable) for observation i
list 6 possible relationships found in scatterplots
- positive linear relationship
- negative linear relationship
- positive curvilinear relationship
- negative curvilinear relationship
- U shaped curvilinear relatnioship
- No relationship
what is the simple linear regression equation: the predicition line and why is it used?
ŷi= b0 + b1Xi
population parameters in practice are estimated
ŷi= predicted value of Y for observation i
- X*i = value of X for observation i
- b*0 = sample Y intercept
- b*1 = sample slope
how do you determine two regression coefficients b0 and b1?
by using least squares estimation
minimises the sum of the squared differences between the actual values Yi and predicted values Yhati using simple linear regression equation
least squares method/solution produces
the line that fits the data with the minimum amount of prediction error
provides line of best fit so SSE is minimised
what does standard error of the estimate show?
measures variability of observed Y values from the predicted Y values
standard deviation around the prediction line
when there is autocorrelation,
there is pattern in residuals. This can put validity of regression model in serious doubt because it obviates the independence of error assumption
eg. after plotting residual, residual fluctuate up and down in cyclical pattern, high chance autocorrelation exists, violating independence of errors assumption
regression coefficients in multiple regression are called…. why?
net regression coefficients. they estimate the predicted change in Y per unit change in a particular X , holding constant the effect of the other X variables
what is a dummy variable regression?
Include categorical variable in a regression model, you use a dummy variable. (converts categorical variable to numerical variable)
Recodes categories of a categorical variable using the numerical values 0 and 1
0 assigned to absence of a characteristic. 1 assigned to presence of characteristic
X2 = 0 if the house does not have fireplace
X2 = 1 if house does have fireplace (substituted in model)
describe interactions in multiregression models
Interaction occurs if effect of an independent variable on the dependent variable changes according to the value of a second independent variable. Interaction between the two indepedent variables
eg. advertising has large effect on sales of product when price of product is low
when there is interaction, what should you do?
use an interaction term (cross-product term) to model an interaction effect in a regression model. Then assess whether the interaction variable makes a significant contribution to the regression model. If significant, cannot use roriginal regression model for prediciton
X3= X1 x X2
Size*fireplacecoded = size x fireplace coded
When the assumptions about residuals are violated, then?
The violation of assumptions means that the regression is invalid and should not be used for prediction or further analysis.
