Lecture 5 Descriptive Statistics Flashcards
What are measures of central tendency include
they are descriptive statistics
mean
median
mode
what is N
number of values
what is the symbol for sum
what is the formula to calculate mean?
how is the mean often written?
The mean is often written as X̄ (“x bar”) — meaning it is the average value of a given variable X.
calculate median
–So, if all values are ranked from 1 to N, the median is the (N+1)/2th value.
–In this case the median is the (25+1)/2th = 13th value: –
what about if the N is odd?
–the median is the average of the two whole numbers either side of this value (e.g., the average of the 12th and 13th values).
what is the mode
value that occurs most frequently
what does the relationship between mean,mode and median depend on
what are distribution of most psychological variables described by?
on the overall distribution of responses.
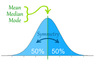
the bell curve
The relationship between measures of central tendency and a response distribution
–When a distribution is skewed the mean, median and mode **will not all be the same. **
–In cases of skew, generally the mean is extremitized in the direction of skew more than the median which is extremitized in the direction of skew more than the mode.
when there is a skew, what is more appropriate statistic to describe central tendency?
why?
the median may be a more appropriate statistic to describe central tendency than the mean
. This is because
(a) the median falls between the mean and mode and (b) the mean can be a very misleading statistic if it differs appreciably from the median or mode.
what does it mean for data to be skewed?
what are two types of skewed data
Data can be “skewed”, meaning it tends to have a long tail on one side or the other:
negative and positive skew
what is a negatively skewed
Because the long “tail” is on the negative side of the peak.
The mean is also on the left of the peak.
distribution is negatively skewed
positively skewed
positive skew is when the long tail is on the positive side of the peak, and some people say it is “skewed to the right”.
The mean is on the right of the peak value.
distribution is positively skewed
normal distribution/ no skew
not skewed.
It is perfectly symmetrical.
And the Mean is exactly at the peak
measures of dispersion
the typical distance of responses from one another.
how tightly clustered are they around the central point?
Measures of dispersion
- Range
The range is simply the difference between the maximum and minimum values.
Measure of dispersion
Mean deviation
average distance of all scores from the mean score
Measures of dispersion
Variation
drawback
drawback: the variance is represented in square units of x, (i.e. x2 )
standard deviation formula
σ = square root (variance)
overcomes the drawback of variance
what does standard of deviation show
if distribution is normally distributed.
but when making statements about samples, the standard deviation will be adjusted by
–sample SD slightly underestimates the SD for the population so an adjustment is required where the SD formula is divided by N-1
standard of deviation formula
statistical inferences
inferential statistics allows us to estimate whether observed diffs between groups are “real” (meaningful) or due to chance.
–We do this by estimating the likelihood of observing the same result purely by chance
Aim of research is to reduce uncertainty to make confident conclusions
what does inferential uncertainty refer to
not knowing whether the patterns we observe in the data (e.g., differences between the means) are informative because they reflect some process of interest, or whether they
are due to a series of chance events
cannot be sure if results were due to chance (just happened to choose a particular sample) or a real difference
what happens if inferential uncertainty is low?
what happens when there is low probability that results are due to chance?
probability is low, then we can conclude that our results are unlikely to be due to chance
then inferential uncertainty is low (greater certainty that results are meaningful)
what is z-score?
z-score is a conversion of our raw score (or mean) into a standardised value.
standardize scores by converting them to z-scores as z-scores are based on standardised normal distribution
This then allows us to compare our score (or group mean) with the rest of the population. eg. **calculate the proportion of scores falling above or below my score **
what is a normal a normal distribution with a mean of 0 and a standard deviation of 1 called?
standard normal distribution
calculate z-score for individual and group
Individual:
score - population mean/ standard deviation
group:
z = sample mean – population mean /
standard error of the mean
sampling distribution of the mean
– would be obtained if we repeatedly took samples from a population and calculated their means.
(a) tend to be normally distributed
(b) less uncertainty than population of individual scores. esp true when sample size gets larger the mean of these distributions stays the same, but the amount of dispersion of these sampling distributions decreases. also according to law of large numbers, smaller standard error (measure of random error)
standard error of mean
used instead of SD to calculate z-score for groups
what happens when the mean is 95 is z score is -1.82?
–1.82 standard error units below the mean.
Why is it more unusual for a group to have mean IQ of 95 than an individual?
based on the formula used, z score for individual with IQ of 95 is -0.33
z score for group with IQ of 95 is -1.82
what happens if there is a very low chance of sampling that mean from population?
we conclude that the sample is probably not drawn from that population but instead belongs to another population.
What is the purpose of z-score?
make inferences about single scores or group means, we want to know how meaningful the result is i.e., in terms of how the score or mean fits with scores or means in the rest of the population.
what are untreated form of data called?
raw data
when there is severe skewness, what is a more appropriate measure of central tendency?
What about of the distribution of data is symmetrical?
median is the best measure of central tendency as it falls between the mean and mode. if distribution is positively skewed, mean will be too positive measure of central tendency and mode will be too negative
mean, mode and median are equal –> mean is the preferred measure
Why is it important to measure spread of scores: measure of dispersion?
examine distribution of data around typical value
what are outliers?
scores that lie far away from typical value for a distribution
symbol for sample mean and population mean
sample SD and greek SD
sample mean: x̄
population mean: μ
Sample SD: SD
Greek: σ
if we do not know population mean or population standard deviation, what is the best estimate?
reasonably large sample mean and standard deviation will provide reasonable estimate of population mean and SD
sampling error
differences between sample and population of interest. error in estimating true value of population of interest
what does a small standard deviation show?
most scores are close to the mean, mean will be a good indicator of each score
what is standardization?
express individual scores in terms of difference (standard deviation units) from mean in order to compare
in s standard normal distribution, what is the mean and standard deviation?
mean is 0 and standard deviation is 1
law of large numbers suggest?
means of large samples will be less dispersed than means of small samples (extreme in small sample can alter the mean)
larger samples are more representative of population at large
reduce uncertainty in form of random error and reduce **inferential uncertainty **
