Brainscape's Knowledge GenomeTM

Browse over 1 million classes created by top students, professors, publishers, and experts.


See full index

ALTIUS > Physics 2 > Flashcards

Physics 2 Flashcards

1
Q

Sound

  • Differentiate b/t Infrasound and Ultrasound
    • Give a real-life example of each
A
  • Infrasound
    • sound of a frequency TOO LOW to be perceived by the human ear.
    • Ex: elephants can perceive infrasonic sounds that humans cannot
  • Ultrasound
    • sound of a frequency TOO HIGH to be perceived by the human ear.
    • Ex: dogs can perceive ultrasonic sounds that humans cannot
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
1
Q
  • Lenses & Mirrors
    • Image Types
      • Differentiate b/t Virtual and Real images wrt location of IMAGE & LIGHT SOURCE
A

Virtual Images

  • there is NO ACTUAL LIGHT emanating from* or *reaching the image
    • Ex: The image formed is behind a plane mirror

Real Images

  • THERE IS ACTUAL LIGHT at the image
    • ex: Image formed on your retina
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

Electricity

  • Conductance
    • Define wrt how they deal with ELECTRON FLOW:
      • conductor
      • resistor
      • insulator
      • semiconductor
      • superconductor
A

CONDUCTOR

  • is a material that allows the flow of electrons through it relatively UNIMPEDED

RESISTOR

  • is a material that tends to IMPEDE the flow of electrons.
    • This being said, even the best conductors do exhibit some small degree of resistance to the flow of electrons
      • superconductors being the possible exception
    • and all resistors do conduct electrons to some small degree

INSULATOR

  • is a material with a very, very high resistivity.
    • There is NO perfect ideal insulator that allows zero current flow under all conditions.
      • However, materials like glass and Teflon allow negligible current flow up to extremely high voltages.

SEMICONDUCTOR

  • is a material thought to be right in the middle of an insulator and a conductor (in terms of conductivity vs. resistivity).

SUPERCONDUCTOR

  • is a material that under very precise conditions is thought to exhibit zero resistance to electron flow
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q
  • Deriving Electric Field equations
    • Force
A
  • For gravity near earth, F=mg
    • ​For a constant elec. field:
      • **F=qE **
  • ​For “real” gravity, F=Gmm/r2​​
    • For a point-charge elec. field:
      • F=Kqq/r2​ (Coulomb’s Law)
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q
  • Lenses & Mirrors
    • The 4 Lens/Mirror Rules
  • (for single-lens systems only!)*
    1. Object distances, p, are always ___
    2. Image distances, q, or focal point distances, f, are
    • ___ if they are on the SAME SIDE as the observer
    • ___if they are on opposite sides
  1. The observer and object are on the:
    • same side for a _____
    • on opposite sides for a ____
  2. Explain “PRI/NVU”
A
  1. Object distances, p, are always (+)
  2. Image distances, q, or focal point distances, f, are
    • (+) if they are on the SAME SIDE as the observer
    • (-) if they are on opposite sides
  3. The observer and object are on the:
    1. same side for a mirror
    2. on opposite sides for a lens
  4. ​PRI/NVU:
    • “Positive, Real, Inverted”
    • “Negative, Virtual, Upright”
    • ALWAYS STAY TOGETHER!!!!!!!!!
      • if you know 1 trait, you know the other 2 by association
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q
  • Electricity
    • Charge
      • Charge is QUANTIZED, according to?
        • (what numerical value)
A
  • e-= 1.6 x 10-19 C
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q
  • Magnetism
    • How do electric fields and magnetic fields relate to each other?
A
  • Changing electric fields create magnetic fields
    • any movement, velocity, rotation, etc. of a charged particle causes a change in the electric field created by that charge
      • thus, creates a magnetic field
  • Changing magnetic fields create **electric fields **
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q
  • Machines
    • Levers
      • Formula=?
A
  • Fm=mg (L1/L2)
    • L1= lever arm for the MASS
    • L2= lever arm for the APPLIED FORCE
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q
  • Circuits
    • Solving circuits using Ohm’s Law
      • What if I can’t adding things together doesnt yield a Simple Circuit?
        • Kirchoff’s Rules!
          • Describe them (2)
A
  • Apply Kirchoff’s rules
    • 1st Rule:
      • current INTO node=current OUT OF node
    • 2nd Rule:
      • In any cyclical circuit, V=0
        • the sum of the voltage drops across each resistor equals the total voltage of the battery
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q
  • Sound
    • General Characteristics
      • How is sound produced?
      • What are its properties as a mechanical wave?
A
  • Sound is always created by a vibrating medium
    • these vibrations propagate through liquids or solids, and generate pressure waves that propagate through GASES (such as air)
  • ​As a mechanical wave, sound CANNOT propagate in a vacuum

​​​

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q
  • Waves
    • The Doppler Effect
      • Describe the “Doppler Shift”
      • Give the 2 formulas
A
  • The Doppler “Shift”
    • perceived by observer
    • dependent on the relative velocity b/t the SOURCE & OBSERVER
      • Greater the relative velocity, greater the shift in frequency or wavelength
  • _​_Δf / fs= v / c
    • ​fs= “source” frequency
  • Δλ/λs= v / c
    • ​λs= “source” wavelength
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q
  • Forms of Energy
    • Kinetic Energy formula
A
  • KE= ½mv2
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q
  • Electric Fields
    • Deriving Electric Field equations
      • how do you get these kinds of equations?
      • what do you need to remember to differentiate between?
A
  • Use conversions for equations you already know for GRAVITY
  • Be sure to differentiate between:
    • CONSTANT Electric Fields
      • are derived by comparison to gravity NEAR EARTH
    • POINT-CHARGE Fields
      • are derived by comparison to “actual” gravity, or gravity IN SPACE
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q
  • Waves
    • Wave speed
      • Formula
      • Name the “3 Cardinal Wave Rules”
A
  • Formula
    • V=λf
  • ​3 CARDINAL WAVE RULES:
  1. ​Wave speed (velocity) is determined BY THE MEDIUM
  2. Frequency NEVER changes when a wave moves from medium to medium
  3. Wavelength DOES change when a wave moves from medium to medium
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q
  • Lenses & Mirrors
    • Give the 3 formulas we need to know:
      • The one for mirrors
      • Thin-Lens equation
      • Magnification equation
    • Wrt (+/-) signs, what does a negative M indicate?
A
  1. **f=½r **(for mirrors only!)
  2. 1/p+1/q=1/f (Thin Lens equation. Good for mirrors also)
  3. **M= -q /p = hq/hp **
  • Negative M= inverted image
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q
  • Waves
    • Superposition of waves
      • The Beat Frequency
        • Occurs when?
          • what do waves need to have very similar to e/o?
        • Give equation
          • fbeat=?
A
  • Occurs when 2 waves with close to the same FREQUENCY interfere with e/o

fbeat= |f1 - f2|

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q
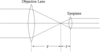
  • Optical Power
    • Describe OP for Two-Lens Systems
      • what are some examples of 2 lens systems?
      • Give formulas for Magnification and Power
A
  • The image formed by the first lens BECOMES THE OBJECT for the second lens
    • Ex: binoculars, telescopes, microscopes, etc.
  • Magnification
    • M=m1m2
  • Power
    • P=p1+p2
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q
  • Sound
    • Harmonics
      • Why does a pipe open at BOTH ends give all harmonics, but a pipe open at one end and closed at the other only gives the odd harmonics?
A
  • For a pipe open at one end and closed at the other, the first harmonic features a node at one end and an antinode at the other.
  • It is impossible to have a node at the open end of a pipe and impossible to have an antinode at the closed end of a pipe.
  • These facts restrict the possible waveforms.
  • The logical “next step,” if you will, to move to the next harmonic from the first one is to add a node—
    • this is impossible, however, because it would require that there be nodes at both ends of the pipe.
    • Thus, we skip this step and add one node and one antinode to get the third harmonic.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q
  • Electric Fields
    • Deriving Elec Field equations
      • PEelec
A
  • For gravity near earth, PEgrav=mgh (height measured against gravity)
    • For a constant elec field:
      • PEelec=qEd (distance measured against strength of elec. field)
  • For “real” gravity, **PEgrav=-Gmm/r **
    • for a point-charge elec field:
      • **PEelec=-Kqq/r ** OR
      • PEelec=Kqq/r
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

Circuits

  • Resistance
    • How can “resistance” be conceptualized/compared to:
      • ____in fluids or ____ between solids
    • Give the Formula for resistance
    • How is Resistance “Temperature Dependent?”
    • The wires b/t any 2 elements in a circuit are assumed to be PERFECT _____S
      • ​wherein resistance=___
      • All resistance occurs where?
A

Resistance can be conceptualized as the equivalent of:

  • DRAG in fluids or FRICTION between solids

R=ρL/A

  • ρ=resistivity
  • L=length
  • A=cross-sectional area

Temperature Dependence

  • Starting around room temp, an increase in temperature results in:
    • a linear increase in resistivity
  • Changing temp is the ONLY WAY you can change resistance in a circuit without replacing the resistor

The wires b/t any 2 elements in a circuit are assumed to be PERFECT CONDUCTORS!

  • resistance=zero
  • all resistance occurs at the resistors
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

Waves

  • Types of Waves
    • Electromagnetic (EM) Waves
      • What kind of medium is req’d for these waves?
      • EM waves are capable of propagating in WHAT?
      • Can they transfer energy, momentum, or both?
      • Are they transverse or longitudinal?
      • Give examples of EM waves
A
  1. NO medium required!
  2. Capable of propagating in a vacuum
  3. Can transfer BOTH energy & momentum

are TRANSVERSE ONLY

Ex: visible light, microwaves, radio waves

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q
  • Wave Speed
    • Wave velocity (v) in various mediums
      • Describe velocity of a wave on a string
        • ​Here, what are its elastic & intertial properties?
        • How does increasing these properties affect V?
A
  • The elastic property (that provides the restoring force in a string)
    • is the string’s TENSION
    • Increased tension always increases velocity.
  • The inertial property
    • is mass per unit length, the “linear mass density”
      • μ: v = √(T/μ).
    • A thicker string (increased mass per length) always decreases velocity (provided the tension stays the same)
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q
  • Waves
    • Superposition of waves
      • Differentiate b/t areas of constructive & descructive interference
A
  • Constructive Interference
    • regions where the amplitudes of superimposed waves ADD TO each other
      • INCREASES amplitude
  • Destructive Interference
    • regions where the amplitudes of superimposed waves SUBTRACT FROM each other
      • DECREASES amplitude
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q
  • Machines
    • What do machines do? What do they never do?
A
  • They reduce the amount of forces necessary to perform a given amount of work
  • They NEVER reduce or change the amount of work
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q
  • Electromagnetic Spectrum
    • Describe Visible Light
      • λ=?
      • Describe RED light (3)
      • Describe Violet light (3)
    • Mnemonic=?
A
  • 390-700nm
  • RED LIGHT
    1. ​​lowest energy
    2. lowest frequency
    3. longest λ
  • VIOLET LIGHT
    1. ​highest energy
    2. highest frequency
    3. shortest λ
  • Mnemonic:
    • ROYGBIV
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
17
Q
  • Machines
    • Ramps
      • Formula
        • What does a “5 meter long” ramp or a “5 meter ramp” imply?
A
  • Fm=mg (h/d)
    • h=height of ramp
    • d=distance along its hypotenuse
    • Fm=force necessary to do the work with the machine
  • “5 meter ramp” or “5 meters long”
    • implies that the _hypotenuse _of the ramp is 5m
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
18
Q
  • Circuits
    • Ohm’s Law
      • Formula
      • What is a common error when manipulating equations using Ohm’s Law?
A
  • Formula
    • V=IR
  • Common error:
    • it CANNOT be said that if voltage increases and current remains constant that resistance will INCREASE
    • Resistance is a permanent quality of the resistor itself
    • The only way to change resistance is to:
    1. physically replace resistors with resistors that have different Ohm’s ratings, or
    2. change the temperature of the resistor
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
19
Q
  • The Law of Conservation of Energy
    • Energy in a/n ____ system is always ____
      • Describe this Law
A
  • Energy in an ISOLATED system is always CONSERVED
    • Energies (KE, PE, Heat Energy, etc.) are frequently transferred back and forth, but **NEVER LOST **
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
20
Q
  • Electric Fields
    • Comparing Elec. Field equations to Gravity
      • What (in gravity equations) equates to what (in elec. field equations)?

Example to start you off:

g (stength of grav. field) = E (strength of electric field)

A
  • g (stength of grav. field)
    • =E (strength of electric field)
  • G (constant)
    • K (constant)
  • h (distance)
    • =r or d
  • m (mass)
    • =q (charge)
  • F (force)
    • =F (same in both)
  • gh (PEgrav)
    • =V (voltage, PEelectrical)
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
21
Q
  • Optical Power
    • Formula (for single-lens systems)
A
  • P=1/f
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
22
Q

Electric Fields

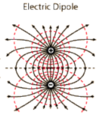
  • Electric Dipoles
    • “a dipole is a _______ of positive & negative charges of ____ _______”
    • What happens when a dipole is exposed to an electric field?
      • What if the dipole DOESNT do the above thing when exposed to B?
      • What does it HAVE, then?
A

a dipole is a separation of positive & negative charges of EQUAL magnitude

When a dipole is exposed to an elec. field, it tends to align itself with that field

  • a dipole that is NOT aligned with the elec. field has PE
    • ​alignment with the field is a lower energy state than alignment AGAINST the field
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
23
Q
  • Electricity
    • Charge
      • Explain “Conservation of Charge”
A
  • The Universe always has a ZERO net charge
  • Charge is created by separation
    • If you separate one electron from a neutral atom, you have created:
      • one independent unit of negative charge (the electron)
      • and simultaneously created one independent unit of **positive **charge (the cation)
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
24
Q

Electric Fields

  • Electric Field Lines
    • Always drawn with their ____s at the POSITIVE charge
    • _____ LINES=STRONGER FIELD
    • Field Lines best approximate “____ flow”
      • What is the opposite of this kind of flow?
A
  • Always drawn with their tails at the positive charge
    • Pointing AWAY FROM, or
    • Pointing TOWARDS the negative charge
  • CLOSER LINES=STRONGER FIELD
  • Field Lines best approximate Current Flow
    • Current flows from positive to negative concentrations

ELECTRON Flow is the opposite (neg.⇒pos.)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
24
Q
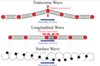
  • Waves
    • Types of Waves
      • compare Transverse vs. Longitudinal waves
A
  • Transverse waves
    • displace the medium perpendicular to their direction of travel
      • ex: EM waves, waves on a string
  • Longitudinal waves
    • displace the medium parallel to their direction of travel
      • ex: sound waves, p-wave earthquakes
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
24
Q
  • Wave Speed
    • Wave Velocity in various mediums
      • velocity of sound waves in a SOLID
        • ​what are the elastic & inertial properties?
        • How do these sound waves differ than the ones going through a gas?
A
  • Elastic property: “Bulk Modulus” (B)
  • Inertial property: Density, ρ
  • Although the densities of solids are typically thousands of times higher than the densities of gases…
    • the elastic moduli are even increased by an even LARGER factor!!
  • This property causes solids to “spring back” extremely quickly following deformation.
  • Sound (compression) waves in solids are therefore TYPICALLY MUCH FASTER THAN SOUND WAVES IN GASES .
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
25
Q
  • Power
    • Formulas
      • Think of power in THIS ORDER (4)
      • Units=?
A
  1. P=ΔE/t
  2. P=W/t
  3. P=Fscosθ
  4. Pi=Fvcosθ
    • gives “instantaneous power”
    • should only be used when asked for specifically
  • ​​Units: Watts
    • J/s
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
26
Q
  • Wave Characteristics
    • Describe
      • wavelength
      • period
      • velocity
      • frequency
      • intensity
      • phase
A
  • Wavelength (units = meters)
    • distance between two adjacent:
      • crests (a.k.a., peaks, maxima),
      • troughs (a.k.a., valleys, minima).
  • Period and frequency are ALWAYS INVERSES OF EACH OTHER!!
  • Velocity
    • how fast the wave moves in space (in m/s).
    • given by v = fλ.
  • Amplitude
    • the “distance” between:
      • the equilibrium point and a crest, or between the equilibrium point and a trough.
  • Intensity is
    • a measure of power per unit area.
      • Waves have power because they transport energy from one point to another in a given amount of time.
  • Intensity is proportional to the square of the amplitude and the square of the frequency.
  • Phase
    • is a relative measure of how closely two waves (typically with the same frequency) are oriented to one another in space,
      • typically expressed in radians or degrees.
      • Two waves that are “in phase” should cross the x-axis at the same point, but may have different amplitudes
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
27
Q
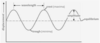
  • Light
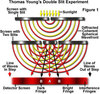
    • Describe how Young’s Double-Slit experiment was physically SET UP
      • ​What needed to happen for his experiment to work?
A
  • Young shone a monochromatic light through a screen with a single slit in it.
    • The purpose of this slit was to create coherent wavefronts
  • Behind the first screen he placed a second screen with two narrow, parallel slits.
    • These created the diffraction pattern.
  • Finally, behind the second screen he placed a third screen.
  • Light traveled through the first two screens and formed alternating pattern of LIGHT and DARK bands on the third screen.

For the experiment to work, the light traveling through each of the 2 slits in the middle screen must be coherent and have the SAME FREQUENCY & POLARIZATION

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
28
Q
  • Electric Fields
    • Think of a “Field” as…?
A
  • FIELD= an invisible influence capable of exerting a FORCE on a:
    • ​mass, or
    • charge
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
30
Q
  • Think of the formulas for WORK in this order (2)
    • If ____ changed, think **WORK! **
A
  1. W=Δ Energy
  2. W=Fdcosθ
  • If ENERGY changed, think WORK!
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
31
Q
  • Lenses & Mirrors
    • Near-Sighted vs Far-Sighted
      • describe
      • Where is the image in relation to the location of the retina?
A
  • Near-sighted (myopia)
    • able to focus clearly on CLOSE objects, but not on distant ones
    • The image is IN FRONT OF the retina
  • Far-sighted (hypertropia)
    • able to focus clearly on DISTANT objects, but not on close ones
    • The image is BEHIND the retina
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
32
Q

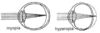
* Light

* Dual nature
    * Define particle & wave models for light
        * What specific experiment/effect **supports** each model?

How are these two models reconciled?

A

The Wave Model of light

supposes that light is a wave

  • Young’s Double Slit Experiment provides support for this model
    • because only waves would show the diffraction and interference patterns necessary to create the characteristic light and dark bands

The Particle Model of light

supposes that light is a particle

  • The photoelectric effect is the major support for this model.
    • Says that electrons are ejected from a material when light of sufficiently high frequency is used—
      • but NOT UNTIL a threshold frequency is reached.

The two are reconciled by:

QUANTUM MECHANICS!

photons are described by “wave functions” which sometimes act as

  • macroscopic waves, and sometimes as
  • macroscopic particles
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
33
Q
  • Waves
    • In order for 2 waves to be “in phase” with each other:
      • What 3 characteristics must they share?
        • Which of these 3 is MOST IMPORTANT?
          • ​What do the 2 waves need to share in order to have this characteristic?
A
  • In order to be 100% in phase, two waves would have to have the same:

1) Frequency,

2) Wavelength

and most importantly

3) TIMING OF MAXIMA/MINIMA

  • which could be done if they share the same time/place of origin)
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
34
Q
  • Light
    • Energy of a Photon
      • Formula
A
  • E=hf
    • h=Plack’s constant (given)
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
35
Q

Waves

  • Types of Waves
    • What are MECHANICAL Waves?
      • 2 traits:
        • What do they require to propagate?
        • Do they transfer energy, momentum, or both?
      • Are they Transverse or Longitudinal or Both?
A
  1. REQUIRE A MEDIUM to propagate
  2. Transfer ENERGY ONLY!!! (not momentum)

Can be BOTH transverse & longitudinal

  1. Transverse
    • transverse mechanical waves require a fairly STIFF MEDIUM in order to propagate
      • ∴ cannot propagate in liquids or gases
    • ex: strings on a musical instrument
  2. Longitudinal
    • ex: sound waves
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
36
Q
  • Define Chemical Energy
A
  • The energy contained within chemical bonds
  • Or the energy stored/released due to the separation and/or flow of ELECTRONS
    • i.e. a battery
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
37
Q
  • Electric Fields
    • What are 2 additional ways to think of “voltage?”
A
  1. ) Voltage =Potential Energy DIVIDED by charge or mass
  2. ) Voltage= whatever “thing” you can MULTIPLY by mass or charge to get Potential Energy
  • Examples:
    • gh*m=mgh=PEgravitational
    • Ed*q=PEelectrical=V*q
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
38
Q

Electromagnetic Spectrum

  • List (in order) each class of the EM spectrum and their relative ENERGIES (10x)
  • Hint:
    • Remember My Interest Varies Under

Xternal Groups

A
  • Radio waves
    • 103
  • Microwaves
    • 10-2
  • Infrared waves
    • 10-5
  • Visible Light
    • 10-6
  • Ultraviolet light
    • 10-8
  • X-rays
    • 10-10
  • Gamma Rays
    • 10-12
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
39
Q

Waves

  • Intensity
    • The Decibel (dB) System
      • Define
      • How is it similar to & differ from the Richter scale (for earthquakes)
A

is a rating system for the intensity of sound within the range of human hearing

Both it and the Richter scale use logarithmic scales

  • Difference:

In short:

10x** increase on Richter Scale = **1 unit increase

10x** increase on dB scale=**10 unit increase

10x increase in earthquake intensity=1.0 unit increase on Richter scale

10x increase in sound intensity=10.0 unit increase on dB scale

  • a sound 10x more intense is 10dB higher
  • a sound 100x more intense is 20 dB higher
  • a sound 1000x more intense is 30 dB higher
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
40
Q
  • Circuits
    • Solving Circuits using Ohm’s Law
      • How to add in series/parallel:
        • Resistors
        • Capacitors
        • Batteries
A
  • Resistors
    • in series:
      • add directly
    • in parallel:
      • add the inverses
      • take the inverse of that sum
  • Capacitors (opposite of solving for resistors)
    • in series:
      • add the inverses
      • take the inverse of that sum
    • In parallel:
      • add directly
  • Batteries
    • in series:
      • add directly
    • in parallel:
      • TOTAL voltage= **the HIGHEST voltage of any one of the batteries in **parallel
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
40
Q
  • Waves
    • Types of Waves
      • List the ones we’re supposed to know
A
  • Transverse vs Longitudinal
  • EM Waves
  • Mechanical Waves
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
40
Q

Sound

  • Sound Resonance
    • Explain how objects have “natural frequencies” and what a “harmonic” is
A

All objects have one or more natural frequencies at which they will vibrate when disturbed.

  • Some objects produce a random array of different vibrational frequencies.
  • Other objects (i.e., musical instruments) vibrate at non-random natural frequencies
    • ​which are integer multiples of a number (e.g. 200Hz, 400Hz, 600Hz, 800Hz).
  • These orderly frequencies are called “HARMONICS”
41
Q
  • W=Δ Energy
    • When you see the following 6 situations, think WORK!​
      • Which of these 6 is the most common example of work you’ll see?
      • ​What’s an important caveat to remember about energy transfer in a system?
A
  1. Change in VELOCITY
    • change in KE=work!
    • most common example!
  2. Change in HEIGHT
    • change in PEgrav = work
  3. Change in POSITION (of masses/planets/etc.) IN SPACE
    • change in PEgrav = work
  4. COMPRESSION of a spring
    • change in PEelastic = work
  5. FRICTION
    • change in internal energy=work
  6. AIR RESISTANCE
    • change in internal energy=work

CAVEAT:

Energy transfer in a system could be due to Heat Transfer as well!!

  • non-conservative forces dissipate some heath energy
    • this leaves LESS energy available to do work
  • Use of word “heat” refers to an increase in the internal energy of the molecules, NOT“heat transfer” (‘Q’ from the first law of Thermodynamics).
42
Q

Sound

  • Drawing Harmonics:
  • For a single vibrating guitar string of the same length*
  • the 1st harmonic is only __ of a __
  • the 2nd harmonic is exactly __ __
  • the 3rd harmonic is __ __
A

The harmonics shown below are all for a single vibrating guitar string of the same length

  • Notice:
    • the 1st harmonic is only ½ of a λ
    • the 2nd harmonic is EXACTLY 1 λ
    • the 3rd harmonic is 1½ λ
43
Q

Waves

  • Define “INTENSITY”
    • ​Give Units
    • How does intensity relate to waves?
    • What is intensity directly proportional to in:
      • SOUND (aka “mechanical”) waves
      • LIGHT waves
A

Intensity= POWER per unit area

Units: Waves/m2

  • Waves often have power (often called “sound power”)
    • because they transfer energy from one location to another w/in a specified time
      • (aka, energy flux)

In sound or mechanical waves, Intensity is *DIRECTLY PROPORTIONAL TO:*

  • ​AMPLITUDE 2
  • FREQUENCY2

*​In LIGHT waves,* intensity is directly proportional to:

  • AMPLITUDE2

But NOT (!!) FREQUENCY2

​

44
Q
  • W=Fdcosθ
    • Think of this definition of work 1st/2nd?
    • Any time a ___ has been applied across a _____, WORK has been done
    • Units=____, which is equivalent to? (2)
A

Think of this definition second

(First should be W= Δ in energy)

  • Any time a force is applied across a displacement, work has been done

Units: Joules, aka:

  • N*m
  • kg*m2 /s-2
45
Q

Intensity

Waves

  • Intensity
    • Why do sound waves create spherical shapes when traveling from their point of origin?
    • MAGNITUDE OF INTENSITY _____es according to ___ of the growing sphere created by sound waves
      • Why? (Has to do with how Intensity is measured; waves/m2)
A
  • Many waves (such as sound) travel outward from their origin in ALL directions SIMULTANEOUSLY*
  • …which creates a wave front in the*
  • shape of a growing sphere*

Magnitude of Intensity DECREASES according to AREA of the growing sphere

  • b/c intensity is measured per square meter

INcreasing m2 leads to a DEcrease in Intensity (ODI)

  • A=4πr2
46
Q
  • Circuits
    • Voltage
      • Think of “voltage” as…?
      • What’s another “intuitive way” of thinking about voltage?
      • 2 formulas
A

Voltage=the amount of PE a system is capable of storing per unit charge

V=PEsys/q

  • Another way:
    • Voltage=the amount of work necessary to move a charge against the electric field
      • moving a longer distance requires more work (voltage increases with distance)

Formulas:

  • V=Ed
  • V=Kq/r
47
Q

Circuits

  • Capacitors
    • The Dialectric
      • Describe what it is and what it does
      • INCREASING Dialectric=_____ing Capacitance
        • Which allows for…?
      • The dialectric must always be a ______or
A

The “dialectric” is the

substance BETWEEN the two plates

  • ALL capacitors have a dialectric, even if it is just air
  • Other dialectrics=gel, composites, etc.
    • once inserted, some energy stored in the capacitor is used to align the polar molecules in the dialectric (ie, dipoles) with the field between the plates
    • Increasing the strength of the dialectric increases the capacitance
      • ​allowing more charge and energy to be stored

INCREASING dialectric=INCREASING capacitance

  • The dialectric must always be an INSULATOR.
48
Q
  • Waves
    • The Doppler Effect
      • Remember these 3 key points:
        • “v” is _____ velocity
        • “c” is the ____ of the ___
        • Does the answer of the equation usually give us that answer we need?
A
  1. The variable v is RELATIVE velocity
    • NOT the velocity of either object
  2. The variable c is the speed of the wave
    • 3 x 108 m/s for light
    • 340 m/s for sound
  3. The answer is of the equation isCHANGE IN λ
    • which is often NOT what they’re asking for!!

This value must be added or subtracted from the initial value in order to get the ACTUAL value due to the doppler effect

  1. Add to the frequency (subtract from the λ) if the relative motion is towards each other
  2. Add to the λ (subtract from the frequency) if the relative motion is away from each other
49
Q
  • Light
    • Young’s Double Slit experiment
      • Equation
      • Define diffraction
A
  • x=λL/ d
    • ​x=distance b/t fringes
    • λ=wavelength of light used
    • d=distance b/t the two slits
    • L=distance b/t double-slit and final screen
  • Diffraction
    • is the tendency of light to spread out as it goes:
      • around a corner, or
      • through a slit
    • equally as important as constructive & destructive interference in Young’s experiment
      • without it, Young’s characteristic interference patterns wouldnt be formed
50
Q
  • Sound
    • Harmonics
      • Formulas (2)
        • Differentiate b/t when to use each
        • show their rearranged forms
A
  • L=nλ/ 2
    • For string or pipe with matching ends
      • Both nodes or both antinodes
    • Gives all nodes
      • n=1,2,3…
    • Rearranged: λ=2L/ n
  • ​L=nλ/ 4
    • ​For one node and one antinode
      • Pipe open at one end ONLY
    • Gives only the **ODD harmonics! **
      • ​n=1,3,5…
    • Rearranged:** λ=4L/ n**
51
Q
  • Circuits
    • Current flows ____ wrt to electron flow?
      • Current formula
    • Current flows from __ to __
    • Electrons flow from __ to __
A
  • Current flows opposite to the direction of electron flow
    • I=Δq/Δt
  • Current flows from positive to negative
  • Electrons flow from **negative to positive **
52
Q
  • Snell’s Law
    • Total Internal Reflection
      • What is the “Critical Angle?”
      • What happens if it is exceeded?
A
  • For waves passing from higher index mediums into lower index mediums, the critical angle is the angle of incidence for which the angle of refraction will be 90°.
  • If this angle is exceeded, refraction ceases and all waves are reflected back into the more dense medium (Total Internal Reflection)
53
Q
  • Torque & Lever Arms
    • Fulcrums & Boards on Strings
      • are simply ___ problems
        • how do you solve?
A
  • are simply equlibrium problems
  • To Solve:
    • set Tclockwise=Tcounterclockwise
      • Include **ALL **torques
        • including T created by mass of the board
      • Force due to mass of the board will act as center of mass
        • will always be the exact linear center of a uniform board
      • Dont forget to set torques equal to e/o, NOT FORCES!!!
        • units: N*m
      • Forces or tensions located exactly at center of rotation do NOT CREATE A TORQUE!! (ignore)
        • ​since r=0
53
Q
  • The Work-Energy Theorem
    • Describe
    • Formula
    • Best to just think of it as…?
A
  • If a net force does work on a rigid object,** **the work done on that object is equal to the change in the KE of the object
  • W= KEfinal- KEinitial
  • Focus on ΔE
    • if you think of it this way, there is no need to use the Work-Energy Theorem
54
Q
  • Forms of Energy
    • Gravitational PE formula
A
  • PEg= -Gmm/r
55
Q
  • Magnetism
    • Give 4 examples of things that involve moving charges, and thus create a magnetic field
A
  1. Nuclei with an odd atomic # or mass #
    • they exhibit nuclear spin
  2. Electrons
    • because they orbit and spin
  3. Current
    • because it IS moving electrons
  4. Bar Magnets
    • usually made of nickel, iron, or other alloy
    • Normally, electrons in a metal are approximately split between spin states
    • In bar magnets, though, they are partially aligned, creating a net magnetic field
57
Q

Electric Fields

  • Equipotential Lines
    • How are they draw in comparison to FIELD LINES?
    • What do Equipotential lines represent?
A
  • Are drawn perpendicular to field lines
  • Represent areas of equal voltage (i.e. electrical potential)
58
Q
  • Electricity
    • Charge
      • What is a BIG MISCONCEPTION about Charge?
A
  • Thinking of positive charges as tiny little “things” with an inherent charge
    • similar to electrons, except positive
      • This is (essentially) a positron
      • Protons also fit this concept
  • FORGET ABOUT POSITRONS & PROTONS when it comes to:
    • ​circuits, electricity, current, etc.
  • Positive charge is ALWAYS:​
    • ​a_ **LACK OF ELECTRONS **_(relative to being neutral)
59
Q
  • Circuits
    • Ohm’s Law across a resistor states that…?
A
  • Voltage drop across _THAT _resistor=current through _THAT _resistor X resistance of _THAT _resistor
60
Q
  • Sound
    • Harmonics
      • Characteristics (3)
      • Frequency of any harmonic is equal to..?
      • For oscillators with matching ends, the λ of the 2nd harmonic equals..?
A
  1. The frequency of the first harmonic is called the “fundamental frequency.”
  2. Each additional harmonic has its own unique frequency and wavelength.
  3. Each harmonic always has one more node, and one more antinode, than the previous harmonic.

The frequency of any harmonic is equal to:

n*fundamental frequency

  • (e.g., if the first harmonic is exactly 200 Hz, the 2nd is 400 Hz, the 3rd is 600 Hz, etc.)

For oscillators with matching ends, the wavelength of the second harmonic equals:

the LENGTH of the string or pipe (λ= L)

61
Q
  • Electric Fields
    • Deriving Elec Field equations
      • Voltage
A
  • For gravity near earth, **V=gh **
    • For a constant elec field:
      • V=Ed (d measured against strength of elec field, E)
  • For “real” gravity, V=Gm/r
    • for a point-charge elec field:
      • V=Kq/r
63
Q
  • Work
    • The 1st Law of Thermodyamics
      • Describe
      • Formula
A
  • Energy change is not ALWAYS due to work
    • some energy is lost to/dissipated as heat
  • ​Work + Heat are the ONLY TWO WAYS energy can be transferred in/out of a system
  • ΔE= W+Q
    • Work=energy transfer due to a force
    • Heath=energy transfer via energy flow from Hot⇒Cold
64
Q
  • Waves
    • Intensity
      • Define “Attenuation”
        • what 2 things cause it in non-dispersive mediums (like EM waves in a vacuum or ideal strings)
A
  • the gradual loss of intensity as a wave passes through a medium
  • ​*
  • In non-dispersive mediums, this is due to scattering (i.e. reflection) of some waves and absorption of wave energy
65
Q

Sound

  • Harmonics
    • What are Overtones?
      • How do they relate to harmonics?
A
  • The terms “1st overtone,” “2nd overtone,” etc., are sometimes used.
    • The 1st overtone is NOT the same as the 1st harmonic!!!!
  • The first harmonic is called
    • the fundamental frequency,
  • the second harmonic is called
    • the 1st overtone
  • the third harmonic is called
    • the 2nd overtone, and so forth.
67
Q
  • Magnetism
    • Think of Magnetism as analogous to ___, with these (3) changes
A
  • Magnetism=analogous to ELECTRICITY, with these changes:
    1. Replace (+) charges with **NORTH **poles
    2. Replace (-) charges with **SOUTH **poles
    3. Magnetic Field lines go from North⇒South, instead of Positive⇒Negative
68
Q
  • Define a system NOT in equilibrium
    • How is solving these problems different than solving for equilibrium problems?
A
  • any problem where the object in question has a NON-ZERO ACCELERATION
    • aka Net Force is NOT zero
  • Solved in the same way as an equilibrium problem, but you add “ma”to the losing side
    • By adding ma to the weaker side we are making them equal again
70
Q
  • Circuits
    • Switches
      • Symbol=?
      • Compare open vs. closed switches
A
  • Symbol: a diagonal break in the line b/t circuit components
  • Open switch
    • **NO **electron flow
  • Closed switch
    • electrons flow
71
Q
  • Torque & Lever Arms
    • What are the 3 formulas we need to remember?
    • in most cases, what should we simply use what equation?
A
  • T=Fl
  • T=mgl
  • T=Frsinθ
    • when force applied isnt perpendicular
      • ​θ isnt 90º
  • rsinθ=l, but only when θ=90º
  • You can usually just use T=Fl
72
Q
  • Circuits
    • Capacitors
      • what do capacitors do?
      • What is their symbol?
      • Formulas
        • Capacitance
        • PE stored by a capacitor
A
  • capacitors store energy and charge by holding electrons on plates separated by a very small distance
  • Symbol: 2 vertical lines of equal length
  • Formulas:
    • Capacitance
      • C=Q/V
    • PE stored by a capacitor
      • U=½CV2​ ​
        • Solve C=Q/V for the missing variable, then plug it into the above equation
        • U=½CV2looks a lot like the KE formula!
73
Q
  • Define Heat Energy
    • what are the 2 common forms you’ll see on the MCAT?
    • What is the term “Heat Energy” almost interchangeable with?
A
  • Energy dissapated as heat
    • on the MCAT, this usually is heat dissapated from a:
      1. collision , or
      2. curent-carrying wire
  • “Heat Energy” ≈ “Internal Energy”
74
Q
  • Circuits
    • Capacitance
      • Affect on capacitance: Increasing…
        • Plate area
        • Plate thickness
        • distance b/t plates
        • strength of the dialectric
        • voltage
A
  • Increasing plate area increases capacitance because there is more room available on the inside surface of the plate to store electrons.
  • Electrons do not line up on the sides or back of the plate, so increasing plate thickness will have no effect on capacitance.
  • Increasing the distance between the plates increases voltage for a given Q on the plates, which decreases capacitance according to C = Q/V.
  • Increasing the strength of the dielectric increases capacitance because the dielectric impedes the buildup of the electric field between the plates and diverts some of the capacitor’s finite energy storage capacity to realign dipoles inside the dielectric.
  • Increased voltage, increases the charge stored but does not increase capacitance, which is the charge stored per voltage.
75
Q
  • Sound
    • Pitch
      • Define
      • What kind of term is “pitch?”
      • what is pitch closely related to?
      • Higher pitch=?
A
  • Pitch is the “perception” of frequency by the human ear
  • Closely related to frequency, but NOT IDENTICAL
  • Is a musical (not scientific) term
  • Sounds with HIGHER PITCH have:
    • ​higher frequencies
  • ​Sounds with LOWER PITCH have:
    • lower frequencies
76
Q
  • Deriving Electric Field equations
    • Strength of the Electric Field
A
  • For gravity *near earth, *g=F/m (from F=mg)
    • for a constant elec field:
      • E=F/q (or E=V/d)
  • For “real” gravity, **g=Gm/r2 **
    • for a point-charge elec field:
      • E=Kq/r2
77
Q
  • Lenses & Mirrors
    • What type of lens is found in:
      • the human eye
      • a magnifying glass
A
  • The lens of the human eye is a converging lens.
    • It creates a real (inverted) image of the object onto the retina.
  • A magnifying glass is also a converging lens
78
Q
  • Waves
    • The Doppler Effect
      • Color Shifts
        • How can the Doppler Effect shift colors?
A
  • If the Dopper Effect causes an INCREASE in frequency (or DECREASE in λ):
    • White light shifts BLUE
  • If the Dopper Effect causes an DECREASE in frequency (or INCREASE in λ):
    • White light shifts RED
79
Q
  • Light
    • Visualizing photons as “light packets,” predict which way light will bend at both boundaries in the scenarios below:
A
80
Q
  • Waves
    • Superposition of Waves
      • Standing Waves
        • describe what creates nodes, anti-nodes, and properties of standing waves
A
  • is a special case of simultaneous CONSTRUCTIVE AND DESTRUCTIVE interference b/t 2 waves
    • have identical frequencies moving through the same medium in opposite directions
  • At points of maximum destructive interference, waves cancel entirely to create a “node”
  • At points of maximum constructive interference, the waves ADD completely to form an “anti-node”
  • Result:
    • is a waveform in which the areas b/t the nodes appear to OSCILLATE up & down b/t crests and troughs
  • A standing wave exhibits NO net transport of energy, and does not itself propagate
    • ​basically, theres no translational mvmt of nodes or anti-nodes in either direction
    • When a standard Traveling wave propagates, the minima & maxima move translationally in the direction of propagation
81
Q
  • Electric Fields
    • What are the 2 types of electric fields?
      • Name & describe
A
  1. Point Charge Fields
    • equate to “real” gravity, or gravity in space
    • A point charge field is an electric field created by a point charge
      • The strength of the electric field varies with the distance (r) from the point charge.
  2. Constant Electric Fields
    • equate to “assumed” gravity, or gravity near earth
    • is constant
      • its strength does **NOT **vary with distance
82
Q
  • Circuits
    • What do you need to do before you can solve for a circuit using Ohm’s Law (V=IR)?
A
  • Create a simple circuit
84
Q
  • Circuits
    • Resistors
      • Symbol=?
      • What always happens when current, I, flows through a resistor?
      • What is “Internal Resistance?”
      • What is current flow like through parallel resistors?
A
  • Symbol=zig-zag line
  • There is ALWAYS a voltage drop across a resistor when current flows through it
  • Internal Resistance
    • batteries experience internal resistance dur to the (inherent) resistivity of their internal components
      • This results in a voltage drop, and therefore **DECREASES **(slightly) THE TERMINAL VOLTAGE OF THE BATTERY
  • ​Current flow through parallel resistors is always *inversely proportional to *resistance
    • if one resistor has 2X the resistance, it will receive ½ the current
86
Q
  • Machines
    • Pulleys
      • Formula=?
      • What should you be cautious for?
A
  • Fm= mg/ (# of vertical ropes directly lifting the mass)​

**CAUTION: **

  • Not every rope that is vertically oriented should be counted and entered into the above equation
  • To be counted, a vertical section of rope must life the mass directly
    • ​either by being attached TO the mass, or
    • by lifting a pulley that is attached to the mass
  • To test, imagine grabbing ONLY THAT ROPE and pulling it upward. Would the mass lift?
87
Q
  • Electromagnetic Spectrum
    • All of these waves (RMIVUXG) are ___?
    • Longer wavelength=?
    • Shorter wavelength=?
A
  • All of these waves are LIGHT!
  • Longer wavelength
    • lower frequency
    • LESS ENERGY
  • Shorter wavelength
    • higher frequency
    • MORE ENERGY
88
Q
  • Light
    • How should be visualize “photons?”
      • Why?
A
  • **AS PHYSICAL PACKETS OF LIGHT! **
    • ​Visualize one of these packages striking a flat boundary at an angle.
    • It is easy to visualize that one corner of our little “light packet” is going to hit the surface first—before the other corner does.
    • If the light is passing from a low index medium to a high index medium, that first corner is suddenly going to be forced to go slower than any other part of the packet that is still in the less dense medium, much like what happens when a car tire goes off the road and hits a soft shoulder.
      • The “light packet” will tend to pivot around the corner that is “stuck” in the higher-index medium.
  • We can intuit exactly which way the light will bend.
90
Q
  • Forms of Energy
    • Elastic PE
A
  • PEelastic= ½kx2
91
Q
  • Lenses & Mirrors
    • Lenses (single-lens systems)
      • Compare Converging & Diverging lenses
        • what do they each usually produce?
        • what about when “p” (obj.) is inside the focal point?
      • What should you assume about Far away objects? (like the moon)
A
  • Converging (aka convex, positive)
    • USUALLY (!!) produces a positive, real, inverted image
    • When “p” is inside the focal point, it produces a negative, virtual, upright image
  • Diverging (aka concave, negative)
    • ALWAYS (!!) produces a negative, virtual, upright image
  • ​Far away objects
    • assume the light hitting the lens are all PARALLEL
    • As object approaches the lens, the image will no longer be exactly at the focal point f
93
Q
  • Think of ENERGY as…?
A
  • The capacity to do WORK
95
Q
  • Machines
    • Force necessary without a machine
      • Formula=?
      • What’s the use of solving for this wrt machines?
A
  • Fnecessary= mg
  • Solving for force needed without a machine helps when comparing it to force needed with a machine
    • Factors will differ by an exact ratio (e.g. 1:5)
96
Q
  • Forms of Energy
    • PE stored in a capacitor (3)
A
  • PEcapacitor= ½ QV
    • PEcapacitor= ½ CV2
      • PEcapacitor=½Q2/C
97
Q
  • Circuits
    • Batteries
      • Symbol=?
      • Think of batteries as…?
      • What do ALL batteries cause?
A
  • Symbol: two vertical lines of UNequal length
    • Longer line= (+) terminal
    • shorter line= (-) terminal
  • Batteries=electron “pumps” that push electrons onto the negative terminal of the battery
    • ​this creates a separation of charge, and therefore a potential difference b/t terminals
      • this drives electron flow around the circuit to the positive terminal
  • All batteries cause A SEPARATION OF CHARGE
    • (which in turn creates a voltage)
98
Q
  • Circuits
    • Household AC current
      • Define:
      • “Root mean square current” (RMS)
        • what is it, how to calculate, etc.
A
  • The “root mean square” (RMS) method of calculating both voltage and current are necessary for alternating current applications because the current and voltage over time are sinusoidal.
  • This creates a problem , because the average of a sine wave centered at the origin is zero.
    • If you randomly sampled the voltage in your household wiring it could literally have a voltage of 120V one instant and a voltage of -120V the next instant.
    • That would average to zero, even though the alternating current does deliver a continuously useful source of power (It can dissipate energy during both cycles).
    • Power companies therefore use the RMS method to calculate the average power delivered to your home
    • RMS is just a mathematical calculation and it can be applied to voltage, current, to sine waves, or even to other waveforms such as square waves.
    • To find RMS, you take readings at various time intervals, square all of those readings, take the average of those squares (i.e., the mean of the squares) and then take the square root of that average.
99
Q
  • Electrical Power
    • Household Electrical Power
      • Name & Describe the 2 types
A
  1. Alternating Current (AC)
    • Both the polarity of the voltage and the direction of the current periodically reverse.
    • A graph of current versus time for an AC current creates a sine wave
  2. Direct Current (DC)
    • Direct flow of current through a circuit from positive to negative
      • (or in terms of electron flow, from negative to positive).
    • DC current is the kind of power used in automobiles because it comes directly from the battery.
      • In fact, if something uses a battery you would be perfectly safe on the MCAT to assume that it must be an example of DC current.
100
Q
  • Magnetism
    • Formula
      • Units
A
  • F=qvBsinθ
    • θ=angle between v and B
  • Units (of B):
    • N*s/C*m OR
    • Kg/A*s2
101
Q
  • Electrical Power
    • Formula
A
  • P=IV
    • Just memorize this one
    • Solve V=IR for the missing variable, then plug it in to get the other two
102
Q
  • Waves
    • Intensity
      • The Decibel System
        • Intensity in dB equation=?
A
  • Intensity (dB)= 10* log ( I / I0)
    • ​I=intensity of the sound wave in (W/m2)
    • I0= threshold of human hearing
      • I0=1 x 10-12 W/m2
      • will always be given
104
Q
  • Define “Internal Energy”
    • what relation do non-conservative forces (such as? Give 2 examples) have with internal energy?
A

The energy of:

  • the internal vibrations*
  • and random motions of molecules and/or atoms*
  • within a system*
  • ​Non-conservative forces (such as friction or drag) acting on a moving object results in the transfer of:

KE⇒ INTERNAL ENERGY

105
Q
  • Systems NOT in equilibrium
    • 2D Forces
A
  • The system we have outlined simplifies everything into up/down or left/right forces.
    • You may well have a force that acts in two-dimensions, say at an angle of 30° to the horizontal.
    • In such cases simply enter into your table the formula that predicts the component of that force that acts up, down, left or right.
106
Q
  • Sound
    • Harmonics
      • Draw diagrams for the first 3 harmonics of:
        1. a pipe open at one end (antinode) and closed at the other end (node)
        2. pipe open at both ends
A
107
Q
  • Mechanical Energy
    • Give the formula
    • What happens to mechanical energy in the absence of non-conservative forces?
A
  • ME=KE+PE
  • ​In the absence of no-conservative forces, Mechanical Energy is CONSERVED
    • ​aka “Total Energy” is conserved
108
Q
  • Wave Speed
    • Wave velocity in various mediums
      • wave speed (v) is typically equal to the ____ of the medium, divided by ____
      • Show this in equation format ^^
        • Describe it a bit
A
  • Wave speed is typically equal to the square root of an ELASTIC property of the medium divided by an INTERTIAL property
  • v = √**(elastic/inertial) **
    • The elastic property is often called a “modulus”.
    • The inertial property is a **type of density. **
111
Q
  • Equilibrium
    • Give 5 examples of equilibrium
A
  1. Terminal velocity (Fair=mg)
  2. constant velocity
  3. Objects at rest
  4. Balanced fulcrums
    • or boards hanging from strings
  5. Objects floating in a liquid
112
Q
  • Snell’s Law
    • Index of Refraction
      • Formula (for I.O.R.)
    • Give Formula for Snell’s Law
    • What does a ray of light being refracted at an interface where n2>n<strong>1</strong> look like?
A
  • Index of Refraction
    • n=c/v
  • Snell’s Law
    • n1sinθ1=n2sinθ2
113
Q

Systems NOT in equilibrium

  • Equilibrium on an Inclined Plane
    • all forces acting down the plane are ____ _____
    • all forces acting up the plane __ _____
    • The force down the plane due to gravity is always F = _____
    • The force of friction is always ______ to the plane _____the direction of motion.
    • There will NEVER be ______ perpendicular to the plane, so you can ignore these forces.
A
  • all forces acting down the plane are “down forces”
  • all forces acting up the plane “up forces.”
  • The force down the plane due to gravity is always F = mgsinθ.
  • The force of friction is always parallel to the plane opposite the direction of motion.
  • There will NEVER be acceleration perpendicular to the plane
    • so you can ignore these forces.
114
Q
  • Forms of Energy
    • Electrical PE (3)
A
  • PEelec= Kqq/r
    • PEelec= qEd
      • PEelec= qV
115
Q
  • Lenses & Mirrors
    • Mirrors
      • For plane mirrors ONLY, the image q and object p will always be…?
A
  • EQUAL DISTANCES on either side of the mirror
116
Q
  • Wave Speed
    • Wave velocity in various mediums
      • Velocity of **sound **waves in a GAS
        • what are the elastic & intertial properties?
        • How does increasing these affect V?
A
  • The elastic property is called the “bulk modulus” (B)
    • directly proportional to **BOTH **
      • ​density and
      • temperature
        • ∴ for gases, the velocity ends up having this “temperature dependence:”
          • v ~ √(T)
  • The inertial property is normal density, ρ
    • v = √(B/ρ)
117
Q
  • Electricity
    • Charge
      • What “is” a (-) and (+) charge?
A
  • Negative (-) Charge=electrons
  • Positive (+) Charge= relatively FEWER electrons
118
Q
  • Snell’s Law
    • Total Internal Reflection
      • Describe
      • What must happen for it to occur?
      • Formula
A
  • For light crossing a boundary from a slower to a faster medium (like from glass or water into air), if the angle of refraction would be 90° or more, the incident light does not enter the second medium at all!!
    • ​100% of the light is reflected off the boundary and back into the first medium.
  • For total internal reflection to occur, the light must be passing from a higher index medium to a lower index medium.
  • Formula
    • n1sinθ1=n2sin_90º_ SO…
    • sinθ1=n2/n1
119
Q

What do TRANSVERSE Mechanical waves require to propagate?

  • ∴ they cannot propagate in ____s or ____s
  • What’s an example of a transverse mechanical wave?
A

Transverse mechanical waves require a fairly STIFF MEDIUM in order to propagate

  • ∴ cannot propagate in liquids or gases
    ex: strings on a musical instrument
120
Q

When solving for Batteries in PARALLEL:

How do you find the TOTAL VOLTAGE?

HINT: It’s easy!

A

Batteries in parallel:

TOTAL voltage=

the HIGHEST voltage of any one of the batteries in parallel

121
Q

Current, I, flows from ____ to _____ concentrations

  • What’s the OPPOSITE of Current Flow?
A

CURRENT FLOW goes from (+)⇒(-)

ELECTRON FLOW is the opposite (-)⇒(+)

122
Q

Sound

  • Sound Resonance

Harmonics (aka “Natural” Frequency)

  • Explain how one object vibrating near another object can cause them both to be in “RESONANCE”, and how “harmonics” factors into all of this
    • What do 2 objects being in resonance CAUSE?
      • ​What in particular that is happening to cause this effect?
A

When one object is vibrating near another object it can cause the neighboring object

to begin vibrating at that SAME frequency

If the exact frequency at which the second object is caused to vibrate happens to be one of its “natural frequencies” (i.e., harmonics):

the two objects are said to be “in resonance”

  • …and via CONSTRUCTIVE interference can produce a much LOUDER sound!

If the first object causes a vibration in the second object that is NOT a match to one of its natural frequencies, resonance does NOT occur

123
Q

_____ing _______ is the ONLY WAY you can change RESISTANCE in a circuit

A

Changing TEMPERATURE is the ONLY WAY you can change resistance in a circuit!

124
Q

The Doppler Effect

  • The answer of the equation will give us is CHANGE IN __?

THIS IS NOT THE ANSWER THEY’LL BE ASKING FOR!!!

  • How do you get the ACTUAL value due to the doppler effect?
    • HINT: It depends if the relative motion is towards/away from each other…
A

Δf/fs = v/c

Δλ/λs = v/c

The answer is of the equation is CHANGE IN λ

  • which is often NOT what they’re asking for!!

This value must be

added or subtracted from the initial value

  • in order to get the ACTUAL value*
  • due to the doppler effect*

If the relative motion is TOWARDS each other:

  • Add to the FREQUENCY
    • (subtract from the λ)

If the relative motion is AWAY FROM each other:

  • Add to the λ
    • (subtract from the frequency)
125
Q
  • A parallel plate capacitor charged to 4 x 10-13C is allowed to discharge for several seconds until it bears a charge of 2.4 x 10-13C*
  • How many electrons flowed off of the capacitor during the discharge?*
A

1.0 x 106C

4E-13 - 2.4E-13=1.6E-13

Divide by 1.6E-19 to get 1E6C

This question requires that you remember the charge on an electron is -1.6 x 10-19C

  • Subtract the final charge from the initial charge and divide by the charge on one electron
    • to get 1.0 x 106C

Remember that electron charge is quantized according to -1.6 x 10-19C

  • In other words, you cannot have a fraction or decimal of an electron
  • In practice, the charge of an electron is so small that generally it is not possible to count individual electrons with precision
    *
126
Q
  • A 20 Coulomb charged particle is dropped into a parallel plate capacitor with very large and distant plates and experiences a force of 250 N*
  • The distance between the plates is 2.0 meters*
  • What is the voltage across the capacitor?*
A

25V

E=F/q** **OR** **E=V/d

To answer this question you must remember that the strength of a field (“E”) is defined by:

  • the force it can exert on a given charge,
    • expressed in:
      • Newtons /Coulomb or
      • Volts /meter
        • (Why? Remember that V = Ed, solve for E)

Calculate E using N/C

  • set that number equal to V/m
    • then solve for V
127
Q

Sound

The frequency of ANY harmonic is equal to?

__ x ___ ____

A

n*fundamental frequency

“Fundamental Frequency”= FIRST harmonic object resonates at

(e.g., if the first harmonic is exactly 200 Hz, the 2nd is 400 Hz, the 3rd is 600 Hz, etc.)

128
Q
  • The first harmonic is called
    • the _____ _______
  • the second harmonic is called
    • the___ _____
  • the third harmonic is called
    • the___ _____
A
  • The first harmonic is called
    • the fundamental frequency,
  • the second harmonic is called
    • the 1st overtone
  • the third harmonic is called
    • the 2nd overtone, and so forth

ALTIUS (27 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2024 Bold Learning Solutions. Terms and Conditions