Topics 10-12 Flashcards
(17 cards)
Explain the drawbacks to using a DV01-neutral hedge for a bond position
- A standard DV01-neutral hedge assumes that the yield on a bond and the yield on a hedging instrument rise and fall by the same number of basis points.
- DV01-style metrics and hedges focus on how rates change relative to one another.
- To improve this DV01-neutral hedge approach, we can apply regression analysis techniques. Using a regression hedge examines the volatility of historical rate differences and adjusts the DV01 hedge accordingly, based on historical volatility.
Describe a regression hedge and explain how it can improve a standard DV01 -neutral hedge.
A regression hedge takes DV01-style hedges and adjusts them for projected nominal yield changes compared to projected real yield changes. Least squares regression analysis, which is used for regression-based hedges, looks at the historical relationship between real and nominal yields.
The advantage of a regression framework is that it provides an estimate of a hedged portfolio’s volatility. An investor can gauge the expected gain in advance and compare it to historical volatility to determine whether the hedged portfolio is an attractive investment.
Calculate the regression hedge adjustment factor, beta
In order to profit from a hedge, we must assume variability in the spread between the real and nominal yields over time. As mentioned, least squares regression is conducted to analyze these changes. The alpha and beta coefficients of a least squares regression line will be determined by the line of best fit through historical yield data points.
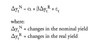
Calculate the face value of an offsetting position needed to carry out a
regression hedge
- This will account for hedging not only the size of the underlying instrument, but also differences between nominal and real yields over time.
- The regression hedge approach assumes that the hedge coefficient, β, is constant over time. This of course is not always the case, so it is best to estimate the coefficient over different time periods and make comparisons.
- !The DV01 hedge is calculated with β = 1!
- Two other factors should be also considered in our analysis:
- (1) the R-squared (i.e., the coefficient of determination). The R-squared gives the percentage of variation in nominal yields that is explained by real yields.
- (2) the standard error of the regression (SER). The standard error of the regression is the standard deviation of the realized error terms in the regression.

Two-variable hedging approach vs. one-security DV01 hedge
- The two-variable approach will provide a better hedge (in terms of R-squared) compared to a single-variable approach.
- However, regression hedging is not an exact science. There are several cases in which simply doing a one-security DV01 hedge, or a two-variable hedge with arbitrary risk weights, is not appropriate (e.g., hedging during a financial crisis).
Compare and contrast level and change regressions

Describe principal component analysis and explain how it is applied to constructing a hedging portfolio
Regression analysis focuses on yield changes among a small number of bonds. Empirical approaches, such as principal components analysis (PCA), take a different approach by providing a single empirical description of term structure behavior, which can be applied across all bonds. PCA attempts to explain all factor exposures using a small number of uncorrelated exposures which do an adequate job of capturing risk.
For example, if we consider the set of swap rates from 1 to 30 years, at annual maturities, the PCA approach creates 30 interest rate factors or components, and each factor describes a change in each of the 30 rates. This is in contrast to regression analysis, which looks at variances of rates and their pairwise correlations.
PCA sets up the 30 factors with the following properties:
- The sum of the variances of the 30 principal components (PCs) equals the sum of the variances of the individual rates. The PCs thus capture the volatility of the set of rates.
- The PCs are not correlated with each other.
- Each PC is chosen to contain the highest possible variance, given the earlier PCs.
The advantage of this approach is that we only really need to describe the volatility and structure of the first three PCs since the sum of the variances of the first three PCs is a good approximation of the sum of the variances of all rates. Thus, the PCA approach creates three factors that capture similar data as a comprehensive matrix containing variances and covariances of all interest rate factors. Changes in 30 rates can now be expressed with changes in three factors, which is a much simpler approach.
Constructing the Binomial Interest Rate Tree (the underlying rule)
There is one underlying rule governing the construction of an interest rate tree:
The values for on-the-run issues generated using an interest rate tree should prohibit arbitrage opportunities.
This means that the value of an on-the-run issue produced by the interest rate tree must equal its market price.
Valuing an Option-Free Bond With the Tree, Using Backward Induction
Backward induction refers to the process of valuing a bond using a binomial interest rate tree.
- The term “backward” is used because in order to determine the value of a bond at node 0, you need to know the values that the bond can take on at node 1.
- For a bond that has N compounding periods, the current value of the bond is determined by computing the bond’s possible values at period N and working “backward” to node 0.
Interest rate drift
In order to equate the discounted value using a binomial tree and the market
price, we need to use what is known as risk-neutral probabilities.
Any difference between the risk-neutral and true probabilities is referred to as the interest rate drift.
Implied drift in the interest rate = RiskNeutralPrup x InterestRateup - RiskNeutralPrdown x InterestRatedown
Using the Risk-Neutral Interest Rate Tree
There are actually two ways to compute bond and bond derivative values using a binomial model. These techniques are referred to as risk-neutral pricing.
- The first method is to start with spot and forward rates derived from the current yield curve and then adjust the interest rates on the paths of the tree so that the value derived from the model is equal to the current market price of an on-the-run bond (i.e., the tree is created to be “arbitrage free”). Once the interest rate tree is derived for an on-the-run bond, we can use it to price derivative securities on the bond by calculating the expected discounted value at each node using the real-world probabilities.
- The second method is to take the rates on the tree as given and then adjust the probabilities so that the value of the bond derived from the model is equal to its current market price. Once we derive these risk-neutral probabilities, we can use them to price derivative securities on the bond by once again calculating the expected discounted value at each node using the risk-neutral probabilities and working backward through the tree.
The value of the derivative is the same under either method.
Explain how the principles of arbitrage pricing of derivatives on fixed income securities can be extended over multiple periods
There are three basic steps to valuing an option on a fixed-income instrument using a binomial tree:
- Step 1: Price the bond value at each node using the projected interest rates.
- Step 2: Calculate the intrinsic value of the derivative at each node at maturity.
- Step 3: Calculate the expected discounted value of the derivative at each node using the risk-neutral probabilities and working backward through the tree.
Note that the option cannot be properly priced using expected discounted values because the call option value depends on the path of interest rates over the life of the option. Incorporating the various interest rate paths will prohibit arbitrage from occurring.
Describe the rationale behind the use of recombining trees in option pricing
In a recombining tree the interest rate in the middle node of period two is the same regardless of the path being up then down or down then up.
It may be the case, in a practical setting, that the up then down scenario produces a different rate than the down then up scenario. An example of this type of tree may result when any interest rate above a certain level (e.g., 3%) causes rates to move a fixed number of basis points, but any interest rate below that level causes rates to move at a pace that is below the up state’s fixed amount. When rates move in this fashion, the movement process is known as state-dependent volatility, and it results in nonrecombining trees.
From an economic standpoint, nonrecombining trees are appropriate; however, prices can be very difficult to calculate when the binomial tree is extended to multiple periods.
Option-adjusted spread (OAS)
The option-adjusted spread (OAS) is the spread that makes the model value (calculated by the present value of projected cash flows) equal to the current market price.
Evaluate the appropriateness of the Black-Scholes-Merton model when
valuing derivatives on fixed income securities
The Black-Scholes-Merton model is the most well-known equity option-pricing model. Unfortunately, the model is based on three assumptions that do not apply to fixed-income securities:
- The model’s main shortcoming is that it assumes there is no upper limit to the price of the underlying asset. However, bond prices do have a maximum value. This upper limit occurs when interest rates equal zero so that zero-coupon bonds are priced at par and coupon bonds are priced at the sum of the coupon payments plus par.
- It assumes the risk-free rate is constant. However, changes in short-term rates do occur, and these changes cause rates along the yield curve and bond prices to change (this is the most troubling assumption of BSM if applied to bond valuation)
- It assumes bond price volatility is constant. With bonds, however, price volatility decreases as the bond approaches maturity.
Callable Bonds
The decline in callable bond yield will reach the point where the rate of increase in the price of the callable bond will start slowing down and eventually level off. This is known as negative convexity.
Callability effectively caps the investor’s capital gains as yields fall. Moreover, it exacerbates reinvestment risk since it increases the cash flow that must be reinvested at lower rates.
As long as yields remain below y’, callable bonds will exhibit price compression, or negative convexity; however, at yields above y’, those same callable bonds will exhibit all the properties of positive convexity.

Putable Bonds
The put feature in putable bonds is another type of embedded option. The put feature gives the bondholder the right to sell the bond back to the issuer at a set price.
As shown in Figure 8, if yields rise above y’, the price of the putable bond does not fall as rapidly as the price of the option-free bond. This is because the put price serves as a floor value for the price of the bond.



