Topics 1-2 Flashcards
1. Estimating Market Risk Measures: An Introduction and Overview 2. Non-parametric Approaches
Geometric return
Assumption is that interim payments are continuously reinvested. Note that this approach ensures that asset price can never be negative.
Some important properties:
- The geometric return implicitly assumes that interim payments are continuously reinvested.
- The geometric return is often more economically meaningful than the arithmetic return, because it ensures that the asset price (or portfolio value) can never become negative regardless of how negative the returns might be. With arithmetic returns, on the other hand, a very low realized return – or a high loss – implies that the asset value P(t) can become negative, and a negative asset price seldom makes economic sense.
- The geometric return is also more convenient. For example, if we are dealing with foreign currency positions, geometric returns will give us results that are independent of the reference currency.
- Similarly, if we are dealing with multiple periods, the geometric return over those periods is the sum of the one-period geometric returns. Arithmetic returns have neither of these convenient properties.
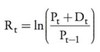
Estimate VaR using a historical simulation approach (formula, how to calculate)
The observation that determines VaR for n observations at the (1 — α ) confidence level would be: (α x n) + 1
Normal VaR
In equation form, the VaR at significance level α is:
Lognormal VaR
The lognormal distribution is right-skewed with positive outliers and bounded below by zero. As a result, the lognormal distribution is commonly used to counter the possibility of negative asset prices (Pt).
The calculation of lognormal VaR (geometric returns) and normal VaR (arithmetic returns) will be similar when we are dealing with short-time periods and practical return estimates.
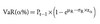
Expected shortfall
A major limitation of the VaR measure is that it does not tell the investor the amount or magnitude of the actual loss. VaR only provides the maximum value we can lose for a given confidence level. The expected shortfall (ES) provides an estimate of the tail loss by averaging the VaRs for increasing confidence levels in the tail. Specifically, the tail mass is divided into n equal slices and the corresponding n — 1 VaRs are computed.
Note that as n increases, the expected shortfall will increase and approach the theoretical true loss.
Coherent risk measures
A more general risk measure than either VaR or ES is known as a coherent risk measure. A coherent risk measure is a weighted average of the quantiles of the loss distribution where the weights are user-specific based on individual risk aversion.
ES (as well as VaR) is a special case of a coherent risk measure. When modeling the ES case, the weighting function is set to [1 / (1 — confidence level)] for all tail losses. All other quantiles will have a weight of zero.
Under expected shortfall estimation, the tail region is divided into equal probability slices and then multiplied by the corresponding quantiles. Under the more general coherent risk measure, the entire distribution is divided into equal probability slices weighted by the more general risk aversion (weighting) function.
This coherent risk measure is more sensitive to the choice of n than expected shortfall, but will converge to the risk measure’s true value for a sufficiently large number of observations. The intuition is that as n increases, the quantiles will be further into the tails where more extreme values of the distribution are located.
Properties of coherent risk measures
Where X and Y represent future values and rho, ρ(.), is the risk measure, a coherent risk measure must meet all four (4) of the following conditions:
- Sub-additivity (the most relevant condition): ρ(X + Y) ≤ ρ(X) + ρ(Y)
- Monotonicity: Y ≥ X → ρ(Y) ≤ ρ(X)
- Positive homogeneity: ρ(λ*X) = λ*ρ(X) for λ > 0
- Translation invariance: ρ(X + c) = ρ(X) – c for some certain amount of n
Both expected shortfall (ES) and value at risk (VaR) are special cases of the general risk measure, however only ES qualifies as a spectral measure; spectral measures are necessarily coherent because (in part) they reflect well-behaved risk-aversion. Expected shortfall is coherent, which implies ES is always sub-additive. Value at risk (VaR) on the other hand, is not a spectral measure: VaR is not always sub-additive (i.e., VaR is only sub-additive if the distribution is elliptical/normal) and therefore VaR is not coherent.
!Non-subadditivity is treacherous because it suggests that diversification might be a bad thing, which would suggest the laughable conclusion that putting all your eggs into one basket might be good risk management practice!
General risk measure
Coherent risk measure is a special case of general risk measure which itself is a weighted average of the quantiles (denoted by qp) of the loss distribution.
Spectral measures are coherent
Evaluate estimators of risk measures by estimating their standard errors
- What happens if we increase the sample size holding all other factors constant? Intuitively, the larger the sample size the smaller the standard error and the narrower the confidence interval.
- Now suppose we increase the bin size, h, holding all else constant. This will increase the probability mass f(q) and reduce p, the probability in the left tail. The standard error will decrease and the confidence interval will again narrow.
- Lastly, suppose that p increases indicating that tail probabilities are more likely. Intuitively, the estimator becomes less precise and standard errors increase, which widens the confidence interval. Note that the expression p(1 — p) will be maximized at p = 0.5
- The quantile-standard-error approach is easy to implement and has some plausibility with large sample sizes. However, it also has weaknesses relative to other methods of assessing the precision of quantile (or VaR) estimators – it relies on asymptotic theory and requires large sample sizes; it can produce imprecise estimators, or wide confidence intervals; it depends on the arbitrary choice of bin width; and the symmetric confidence intervals it produces are misleading for extreme quantiles whose ‘true’ confidence intervals are asymmetric reflected the increasing sparsity of extreme observations as we move further out into the tail.”
- Heavy tails might make ES estimators in general less accurate than VaR estimators. There are grounds to think that such a conclusion might be overly pessimistic.
- The standard error of any estimator of a coherent risk measure will vary from one situation to another, and the best practical advice is to get into the habit of always estimating the standard error whenever one estimates the risk measure itself.
- An alternative approach to the estimation of standard errors for estimators of coherent risk measures is to apply a bootstrap: we bootstrap a large number of estimators from the given distribution function (which might be parametric or non-parametric, e.g., historical); and we estimate the standard error of the sample of bootstrapped estimators.
Quantile-quantile (QQ) plot
The quantile-quantile (QQ) plot is a straightforward way to visually examine if empirical data fits the reference or hypothesized theoretical distribution.
A QQ plot is useful in a number of ways:
- First, if the data are drawn from the reference population, then the QQ plot should be linear. We can therefore use a QQ plot to form a tentative view of the distribution from which our data might be drawn. In this way, a linear QQ plot indicates a good fit to the distribution.
- Second, because a linear transformation in one of the distributions in a QQ plot merely changes the intercept and slope of the QQ plot, we can use the intercept and slope of a linear QQ plot to give us a rough idea of the location and scale parameters of our sample data.
- Third, if the empirical distribution has heavier tails than the reference distribution, the QQ plot will have steeper slopes at its tails, even if the central mass of the empirical observations is approximately linear. A QQ plot where the tails have slopes different than the central mass is therefore suggestive of the empirical distribution having heavier, or thinner, tails than the reference distribution.
Other:
- Like kurtosis, skew CAN be visualized and manifests as an arched pattern.
- We can use the intercept and slope of a linear QQ plot to give us a rough idea of the location and scale parameters of our sample data.
- QQ plot is good for identifying outliers even if the other observations are broadly consistent with the reference distribution
Parametric approaches to estimating VAR
We can think of parametric approaches as fitting curves through the data and then reading off the VaR from the fitted curve.
In making use of a parametric approach, we therefore need to take account of both the statistical distribution and the type of data to which it applies.
Bootstrap historical simulation
- The bootstrap historical simulation is a simple and intuitive estimation procedure. In essence, the bootstrap technique draws a sample from the original data set, records the VaR from that particular sample and “returns” the data. This procedure is repeated over and over and records multiple sample VaRs. Since the data is always “returned” to the data set, this procedure is akin to sampling with replacement. The best VaR estimate from the full data set is the average of all sample VaRs.
- Empirical analysis demonstrates that the bootstrapping technique consistently provides more precise estimates of coherent risk measures than historical simulation on raw data alone.
- A bootstrapped estimate will often be more accurate than a ‘raw’ sample estimate, and bootstraps are also useful for gauging the precision of estimates.
- Perhaps the main limitation of the bootstrap is that standard bootstrap procedures presuppose that observations are independent over time, and they can be unreliable if this assumption does not hold
Describe historical simulation using non-parametric density estimation
- The clear advantage of the traditional historical simulation approach is its simplicity.
- One obvious drawback, however, is that the discreteness of the data does not allow for estimation of VaRs between data points. With n observations, the historical simulation method only allows for n different confidence levels.
- One of the advantages of non-parametric density estimation is that the underlying distribution is free from restrictive assumptions. Therefore, the existing data points can be used to “smooth” the data points to allow for VaR calculation at all confidence levels. The simplest adjustment is to connect the midpoints between successive histogram bars in the original data sets distribution. See Figure for an illustration of this surrogate density function. Notice that by connecting the midpoints, the lower bar “receives” area from the upper bar, which “loses” an equal amount of area. In total, no area is lost, only displaced, so we still have a probability distribution function, just with a modified shape.
Age-weighted Historical Simulation
- The decay parameter, λ, can take on values 0 < λ < 1 where values close to 1 indicate slow decay.
- The implication of the age-weighted simulation is to reduce the impact of ghost effects and older events that may not reoccur. Note that this more general weighting scheme suggests that historical simulation is a special case where λ = 1 (i.e., no decay) over the estimation window.
- This approach is also known as the hybrid approach.
- It generalizes standard historical simulation (HS) because “we can regard traditional HS as a special case with zero decay, or λ →1.
- A suitable choice of lambda (λ) can make the VaR (or ES) estimates more responsive to large loss observations: a large loss event will receive a higher weight than under traditional HS, and the resulting next-day VaR would be higher than it would otherwise have been.
- Age-weighting helps to reduce distortions caused by events that are unlikely to recur, and helps to reduce ghost effects.
- We can modify age-weighting in a way that makes our risk estimates more efficient and effectively eliminates any remaining ghost effects. Age-weighting allows us to let our sample period grow with each new observation, so we never throw potentially valuable information away. So, there would be no ‘jumps’ in our sample resulting from old observations being thrown away.
- However, age-weighting also reduces the effective sample size, other things being equal, and a sequence of major profits or losses can produce major distortions in its implied risk profile.
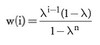
Volatility-weighted Historical Simulation
Another approach is to weight the individual observations by volatility rather than proximity to the current date. The intuition is that if recent volatility has increased, then using historical data will underestimate the current risk level. Similarly, if current volatility is markedly reduced, the impact of older data with higher periods of volatility will overstate the current risk level.
This approach can be combined with the age-weighted approach to increase the sensitivity of risk estimates to large losses, and to reduce the potential for distortions and ghost effects. It can also be combined with order statistics or bootstrap methods to estimate confidence intervals for VaR or ES.
There are several advantages of the volatility-weighted method:
- First, it explicitly incorporates volatility into the estimation procedure in contrast to other historical methods.
- Second, the near-term VaR estimates are likely to be more sensible in light of current market conditions.
- Third, the volatility-adjusted returns allow for VaR estimates that are higher than estimates with the historical data set.
Algorithm:
- Each historical return(t) is replaced by: return(t)*volatility(0)/volatility(t).
- Then conduct typical historical simulation (HS) on adjusted return series
Spectral Risk Measure and its features
- An advantage of SRM over ES and VaR is that SRMs are not bound to a single confidence level.
- Spectral risk measures are a promising generalization of expected shortfall. The main advantages are improved smoothness and the intuitive link to risk aversion. If the underlying risk model is simulations-based, the additional calculation effort as opposed to ES seems negligible.
- The weight, w, must be (weakly) increasing over [0,1].
- An increasing weight, w, over [0,1] ensures the SRM is coherent.
- The increasing weight is significant: “This restriction [i.e., weakly increasing weight] also implies that larger losses are taken more seriously than smaller losses and thus the function establishes a relationship to risk aversion. The intuition is that a financial institution is not very risk averse for small losses, which can be absorbed by income, but becomes increasingly risk averse to larger losses.”
