Revision Flashcards
(27 cards)
Protective Put
Holding an asset and a put on the asset is a strategy known as a protective put.
Value at expiration: VT = ST + max(0,X – ST)
Profit: Π = VT – S0 – p0
Maximum profit = ∞
Maximum loss = S0 + p0 – X
Breakeven: ST* = S0 + p0
You can use a protective put to limit the downside risk at the cost of the put premium

Covered Call
An option strategy involving the holding of an asset and sale of a call in the asset.
Value at expiration: VT = ST – max(0,ST – X)
Profit: Π = VT – S0 + c0
Maximum profit = X – S0 + c0
Maximum loss = S0 – c0
Breakeven: ST* = S0 – c0
Finally, we should note that anecdotal evidence suggests that writers of call options make small amounts of money, but make it often. The reason for this phenomenon is generally thought to be that buyers of calls tend to be overly optimistic, but that argument is fallacious. The real reason is that the expected profits come from rare but large payoffs.
Following this line of reasoning, however, it would appear that sellers of calls can consistently take advantage of buyers of calls. That cannot possibly be the case. What happens is that buyers of calls make money less often than sellers, but when they do make money, the leverage inherent in call options amplifies their returns. Therefore, when call writers lose money, they tend to lose big, but most call writers own the underlying or are long other calls to offset the risk.

Bull Spreads
A bull spread is designed to make money when the market goes up. In this strategy we combine a long position in a call with one exercise price and a short position in a call with a higher exercise price.
To summarize the bull spread, we have:
Value at expiration: VT = max(0,ST – X1) – max(0,ST – X2)
Profit: Π = VT – c1 + c2
Maximum profit = X2 – X1 – c1 + c2
Maximum loss = c1 – c2
Breakeven: ST* = X1 + c1 – c2
Bull spreads are used by investors who think the underlying price is going up.

Bear Spreads
If one uses the opposite strategy, selling a call with the lower exercise price and buying a call with the higher exercise price, the opposite results occur. The graph is completely reversed: The gain is on the downside and the loss is on the upside. This strategy is called a bear spread. The more intuitive way of executing a bear spread, however, is to use puts. Specifically, we would buy the put with the higher exercise price and sell the put with the lower exercise price.
To summarize the bear spread, we have
Value at expiration: VT = max(0,X2 – ST) – max(0,X1 – ST)
Profit: Π = VT – p2 + p1
Maximum profit = X2 – X1 – p2 + p1
Maximum loss = p2 – p1
Breakeven: ST* = X2 – p2 + p1
The bear spread with calls involves selling the call with the lower exercise price and buying the one with the higher exercise price. Because the call with the lower exercise price will be more expensive, there will be a cash inflow at initiation of the position and hence a profit if the calls expire worthless.

Butterfly Spreads
In both the bull and bear spread, we used options with two different exercise prices. There is no limit to how many different options one can use in a strategy. As an example, the butterfly spread combines a bull and bear spread. Consider three different exercise prices, X1, X2, and X3. Suppose we first construct a bull spread, buying the call with exercise price of X1 and selling the call with exercise price of X2. Recall that we could construct a bear spread using calls instead of puts. In that case, we would buy the call with the higher exercise price and sell the call with the lower exercise price. This bear spread is identical to the sale of a bull spread.
In summary, for the butterfly spread
Value at expiration: VT = max(0,ST – X1) – 2max(0,ST – X2) + max(0,ST – X3)
Profit: Π = VT – c1 + 2c2 – c3
Maximum profit = X2 – X1 – c1 + 2c2 – c3
Maximum loss = c1 – 2c2 + c3
Breakeven: ST* = X1 + c1 – 2c2 + c3 and ST* = 2X2 – X1 – c1 + 2c2 – c3
Butterfly spread is a strategy based on the expectation of low volatility in the underlying. Of course, for a butterfly spread to be an appropriate strategy, the user must believe that the underlying will be less volatile than the market expects. If the investor buys into the strategy and the market is more volatile than expected, the strategy is likely to result in a loss. If the investor expects the market to be more volatile than he believes the market expects, the appropriate strategy could be to sell the butterfly spread. Doing so would involve selling the calls with exercise prices of X1 and X3 and buying two calls with exercise prices of X2.

Straddle
Suppose the investor buys both a call and a put with the same exercise price on the same underlying with the same expiration. This strategy enables the investor to profit from upside or downside moves. Its cost, however, can be quite heavy. In fact, a straddle is a wager on a large movement in the underlying.
Only when the investor believes the market will be more volatile than everyone else believes would a straddle be advised.
In summary, for a straddle:
Value at expiration: VT = max(0,ST – X) + max(0,X – ST)
Profit: Π = VT – (c0 + p0)
Maximum profit = ∞
Maximum loss = c0 + p0
Breakeven: ST* = X ± (c0 + p0)
As we have noted, a straddle would tend to be used by an investor who is expecting the market to be volatile but does not have strong feelings one way or the other on the direction. An investor who leans one way or the other might consider adding a call or a put to the straddle. Adding a call to a straddle is a strategy called a strap, and adding a put to a straddle is called a strip. It is even more difficult to make a gain from these strategies than it is for a straddle, but if the hoped-for move does occur, the gains are leveraged. Another variation of the straddle is a strangle, in which the put and call have different exercise prices. This strategy creates a graph similar to a straddle but with a flat section instead of a point on the bottom.

Strangle
An investor purchases a call on a stock, with an exercise price of $50 and a premium of $1.50, and purchases a put option with the same maturity that has an exercise price of $45 and a premium of $2. Compute the payoff of a strangle strategy if the stock is at $40.
A strangle (or bottom vertical combination) is similar to a straddle except that the options purchased are slightly out-of-the-money, so it is cheaper to implement than the straddle. The payoff is similar to the straddle except for a flat section between the strike prices, as shown in Figure 8. Because it is cheaper, the stock will have to move more relative to the straddle before the strangle pays off. Strangles are also symmetric around the strikes.
Answer:
profit = max(0, ST — XH) + max(0, XL—ST) — C0 — P0
profit = max(0,40 —$50) + max(0,45 — 40) —1.50 —2 = $1.50

Collars
In effect, the holder of the asset gains protection below a certain level, the exercise price of the put, and pays for it by giving up gains above a certain level, the exercise price of the call. This strategy is called a collar. When the premiums offset, it is sometimes called a zero-cost collar.
In summary, for the collar:
Value at expiration: VT = ST + max(0,X1 – ST) – max(0,ST – X2)
Profit: Π = VT – S0
Maximum profit = X2 – S0
Maximum loss = S0 – X1
Breakeven: ST* = S0
Collars are virtually the same as bull spreads.

Box Spreads
A box spread can also be used to exploit an arbitrage opportunity but it requires that neither the binomial nor Black–Scholes–Merton model holds, it needs no estimate of the volatility, and all of the transactions can be executed within the options market, making implementation of the strategy simpler, faster, and with lower transaction costs.
In basic terms, a box spread is a combination of a bull spread and a bear spread. Suppose we buy the call with exercise price X1 and sell the call with exercise price X2. This set of transactions is a bull spread. Then we buy the put with exercise price X2 and sell the put with exercise price X1. This is a bear spread. Intuitively, it should sound like a combination of a bull spread and a bear spread would leave the investor with a fairly neutral position, and indeed, that is the case.
(X2−X1)/(1+r)T=c1−c2+p2−p1
If some combination of the options was such that the net premium is more than the present value of the payoff, then the box spread would be overpriced.
So to summarize the box spread, we say that
Value at expiration: VT = X2 – X1
Profit: Π = X2 – X1 – (c1 – c2 + p2 – p1)
Maximum profit = (same as profit)
Maximum loss = (no loss is possible, given fair option prices)
Breakeven: no breakeven; the transaction always earns the risk-free rate, given fair option prices
Compute the value of a European option using the Black-Scholes-Merton model on a non-dividend-paying stock

Calculation option delta using BSM
To completely hedge a long stock or short call position, an investor must purchase the number of shares of stock equal to delta times the number of options sold. Another term for being completely hedged is delta-neutral.
- if you buy a call or a put option that is just out of the money (i.e. the strike price of the option is above the price of the underlying if the option is a call, and below the price of the underlying if the option is a put), then the option will always have a delta value that is somewhere between 1.0 and –1.0.
- Generally speaking, an at-the-money option usually has a delta at approximately 0.5 or -0.5.
- Call delta values range from 0 to 1.0, while put delta values range from 0 to –1.0.
- As the option gets further in the money, delta approaches 1.00 on a call and –1.00 on a put.
The commodity term structure of volatility for some commodities is flat for other is steep. Why?
The effect on volatility term structure is highest when storage cost and/or convenience yield is high.
- Financial assets tend to have neither: “for financial assets, volatilities are driven by spot prices, which implies basically constant volatilities across maturities.”
- “The effect [i.e., volatilities decreasing with maturity] is strongest for less storable [i.e., costly to store] products such as energy products and less so for base metals.”
Exponentially weighted moving average (EWMA) model
The exponentially weighted moving average (EWMA) model is a specific case of the general weighting model. The main difference is that the weights are assumed to decline exponentially back through time. This assumption results in a specific relationship for variance in the model:
σn2 = λσn-12 + (1 - λ)un-12
where:
λ = weight on previous volatility estimate (λ between zero and one)
The simplest interpretation of the EWMA model is that the day-n volatility estimate is calculated as a function of the volatility calculated as of day n — 1 and the most recent squared return. Depending on the weighting term X, which ranges between zero and one, the previous volatility and most recent squared returns will have differential impacts. High values of λ will minimize the effect of daily percentage returns, whereas low values of λ will tend to increase the effect of daily percentage returns on the current volatility estimate.
One benefit of the EWMA is that it requires few data points. Specifically, all we need to calculate the variance is the current estimate of the variance and the most recent squared return.

GARCH(1,1) model

EWMA - the idea

Define and compute the DV01 of a fixed income security given a change in yield and the resulting change in price

Define, compute, and interpret the effective duration of a fixed income security given a change in yield and the resulting change in price
Macaulay duration is an estimate of a bond’s interest rate sensitivity based on the time, in years, until promised cash flows will arrive. Since a 5-year zero-coupon bond has only one cash flow five years from today, its Macaulay duration is five.
Periodic market yield = YTM / number of coupon periods per year

Compare and contrast DV01 and effective duration as measures of price sensitivity.

Proxy for convexity of a bond
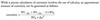
Modified duration and Macaulay of perpetuity bond with a coupon i and YTM y, compounding factor n
Modified:
D = 1/i
Macalay:
Dmacaulay = (1+y/n)/i
Unexpected loss (UL) formula
UL = EAD*SQRT[PD*variance(LGD) + LGD2*variance(PD)],
such that UL is non-linear with respect to PD, volatility (PD) and LGD
Risk-neutral probability
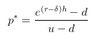
Define and calculate unexpected loss (UL). Estimate the variance of default probability assuming a binomial distribution.

UL of portfolio of loans and contribution of each loan to the portfolio UL



