Tree Depth First Search Strategies

Question 1

Binary Tree Path Sum

Given a binary tree and a number ‘S’, find if the tree has a path from root-to-leaf such that the sum of all the node values of that path equals ‘S’.

Answer 1

As we are trying to search for a root-to-leaf path, we can use the Depth First Search (DFS) technique to solve this problem.

To recursively traverse a binary tree in a DFS fashion, we can start from the root and at every step, make two recursive calls one for the left and one for the right child.

Here are the steps for our Binary Tree Path Sum problem:

1. Start DFS with the root of the tree.
2. If the current node is not a leaf node, do two things:
   
   • Subtract the value of the current node from the given number to get a new sum => S = S - node.value
   • Make two recursive calls for both the children of the current node with the new number calculated in the previous step.
3. At every step, see if the current node being visited is a leaf node and if its value is equal to the given number ‘S’. If both these conditions are true, we have found the required root-to-leaf path, therefore return true.
4. If the current node is a leaf but its value is not equal to the given number ‘S’, return false.

The time complexity of the above algorithm is O(N), where ‘N’ is the total number of nodes in the tree. This is due to the fact that we traverse each node once.

The space complexity of the above algorithm will be O(N) in the worst case. This space will be used to store the recursion stack. The worst case will happen when the given tree is a linked list (i.e., every node has only one child).

Question 2

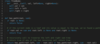
All Paths for a Sum

Given a binary tree and a number ‘S’, find all paths from root-to-leaf such that the sum of all the node values of each path equals ‘S’.

Answer 2

This problem follows the Binary Tree Path Sum pattern. We can follow the same DFS approach. There will be two differences:

1. Every time we find a root-to-leaf path, we will store it in a list.
2. We will traverse all paths and will not stop processing after finding the first path.

The time complexity of the above algorithm is O(N​²​​), where ‘N’ is the total number of nodes in the tree. This is due to the fact that we traverse each node once (which will take O(N)), and for every leaf node we might have to store its path which will take O(N).

We can calculate a tighter time complexity of O(NlogN) from the space complexity discussion below.

If we ignore the space required for the allPaths list, the space complexity of the above algorithm will be O(N) in the worst case. This space will be used to store the recursion stack. The worst case will happen when the given tree is a linked list (i.e., every node has only one child).

Question 3

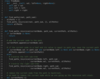
Sum of Path Numbers

Given a binary tree where each node can only have a digit (0-9) value, each root-to-leaf path will represent a number. Find the total sum of all the numbers represented by all paths.

Answer 3

This problem follows the Binary Tree Path Sum pattern. We can follow the same DFS approach. The additional thing we need to do is to keep track of the number representing the current path.

How do we calculate the path number for a node? Taking the first example mentioned above, say we are at node ‘7’. As we know, the path number for this node is ‘17’, which was calculated by: 1 * 10 + 7 => 17. We will follow the same approach to calculate the path number of each node.

The time complexity of the above algorithm is O(N), where ‘N’ is the total number of nodes in the tree. This is due to the fact that we traverse each node once.

The space complexity of the above algorithm will be O(N) in the worst case. This space will be used to store the recursion stack. The worst case will happen when the given tree is a linked list (i.e., every node has only one child).

Question 4

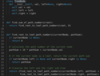
Path With Given Sequence

Given a binary tree and a number sequence, find if the sequence is present as a root-to-leaf path in the given tree.

Answer 4

This problem follows the Binary Tree Path Sum pattern. We can follow the same DFS approach and additionally, track the element of the given sequence that we should match with the current node. Also, we can return false as soon as we find a mismatch between the sequence and the node value.

The time complexity of the above algorithm is O(N), where ‘N’ is the total number of nodes in the tree. This is due to the fact that we traverse each node once.

The space complexity of the above algorithm will be O(N) in the worst case. This space will be used to store the recursion stack. The worst case will happen when the given tree is a linked list (i.e., every node has only one child).

Question 5

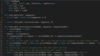
Count Paths for a Sum

Given a binary tree and a number ‘S’, find all paths in the tree such that the sum of all the node values of each path equals ‘S’. Please note that the paths can start or end at any node but all paths must follow direction from parent to child (top to bottom).

Answer 5

This problem follows the Binary Tree Path Sum pattern. We can follow the same DFS approach. But there will be four differences:

1. We will keep track of the current path in a list which will be passed to every recursive call.
2. Whenever we traverse a node we will do two things: 1) Add the current node to the current path. 2) As we added a new node to the current path, we should find the sums of all sub-paths ending at the current node. If the sum of any sub-path is equal to ‘S’ we will increment our path count.
3. We will traverse all paths and will not stop processing after finding the first path.
4. Remove the current node from the current path before returning from the function. This is needed to Backtrack while we are going up the recursive call stack to process other paths.

The time complexity of the above algorithm is O(N​²​​) in the worst case, where ‘N’ is the total number of nodes in the tree. This is due to the fact that we traverse each node once, but for every node, we iterate the current path. The current path, in the worst case, can be O(N) (in the case of a skewed tree). But, if the tree is balanced, then the current path will be equal to the height of the tree, i.e., O(logN). So the best case of our algorithm will be O(NlogN).

The space complexity of the above algorithm will be O(N). This space will be used to store the recursion stack. The worst case will happen when the given tree is a linked list (i.e., every node has only one child). We also need O(N) space for storing the currentPath in the worst case.

Overall space complexity of our algorithm is O(N).

Question 6

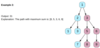
Tree Diameter

Given a binary tree, find the length of its diameter. The diameter of a tree is the number of nodes on the longest path between any two leaf nodes. The diameter of a tree may or may not pass through the root.

Answer 6

This problem follows the Binary Tree Path Sum pattern. We can follow the same DFS approach. There will be a few differences:

1. At every step, we need to find the height of both children of the current node. For this, we will make two recursive calls similar to DFS.
2. The height of the current node will be equal to the maximum of the heights of its left or right children, plus ‘1’ for the current node.
3. The tree diameter at the current node will be equal to the height of the left child plus the height of the right child plus ‘1’ for the current node: diameter = leftTreeHeight + rightTreeHeight + 1. To find the overall tree diameter, we will use a class level variable. This variable will store the maximum diameter of all the nodes visited so far, hence, eventually, it will have the final tree diameter.

The time complexity of the above algorithm is O(N), where ‘N’ is the total number of nodes in the tree. This is due to the fact that we traverse each node once.

The space complexity of the above algorithm will be O(N) in the worst case. This space will be used to store the recursion stack. The worst case will happen when the given tree is a linked list (i.e., every node has only one child).

Question 7

Path with Maximum Sum

Find the path with the maximum sum in a given binary tree. Write a function that returns the maximum sum. A path can be defined as a sequence of nodes between any two nodes and doesn’t necessarily pass through the root.

Answer 7

This problem follows the Binary Tree Path Sum pattern and shares the algorithmic logic with Tree Diameter. We can follow the same DFS approach. The only difference will be to ignore the paths with negative sums. Since we need to find the overall maximum sum, we should ignore any path which has an overall negative sum.

The time complexity of the above algorithm is O(N), where ‘N’ is the total number of nodes in the tree. This is due to the fact that we traverse each node once.

The space complexity of the above algorithm will be O(N) in the worst case. This space will be used to store the recursion stack. The worst case will happen when the given tree is a linked list (i.e., every node has only one child).