Dynamic Programming Strategies Flashcards by John Smith

Largest Sum Subarray

Given an array, find the contiguous subarray with the largest sum.

Linear runtime, Constant memory

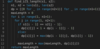
The basic idea of Kadane’s algorithm is to scan the entire array and at each position find the maximum sum of the subarray ending there. This is achieved by keeping a current maximum for the current array index and a global maximum. The algorithm is as follows:

current_max = A[0]
global_max = A[0]
for i = 1 -> size of A
if current_max is less than 0
then current_max = A[i]
otherwise
current_max = current_max + A[i]
if global_max is less than current_max
then global_max = current_max

How well did you know this?

Not at all

Perfectly

MaxSum Subsequence - Nonadjacent Elements

Find an efficient algorithm to find the maximum sum of a subsequence in an array so that no consecutive elements are part of this subsequence. Consider the following examples; the max sums of a subsequence with no consecutive elements in the below examples are 25 and 9 respectively.

Linear runtime, linear memory.

Iterate over the entire input array, and in every iteration pick the maximum of these two values:

Max Sum of the last iteration
Max Sum of second last iteration + current iteration index.

This solution can be improved further by reducing the space usage. We don’t need to keep an array of previous maximum sums, only storing the last two sums would suffice. Also, the algorithm can be modified to track all the indices of this subarray with some additional data structures.

How well did you know this?

Not at all

Perfectly

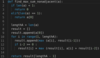
Game Scoring: Find the Number of Ways a Player can Score ‘n’ Runs

Imagine a game (like baseball) where a player can score 1,2, or 4 runs. Given a score, “n”, find the total number of ways score “n” can be reached.

We’ll use the dynamic programming approach to build the solution bottom-up. We’ll store the results in a fixed size array. Scoring options are 1, 2, and 4. The maximum score is 4, so we need to save the last four ways to calculate the number of ways for a given ‘n’. On each iteration, the result will be the sum of values present at the 3rd, 2nd, and 0th index of the results array. This is because the result at ‘n’ is the sum of values at n-1, n-2 and n-4. We’ll slide the results towards the left and save the current result at the last index.

How well did you know this?

Not at all

Perfectly

Levenshtein Distance

Given two strings, compute the Levenshtein distance between them, meaning the minimum number of edits required to convert one string to the other.

For example, the Levenshtein distance between “kitten” and “sitting” is 3.

The minimum steps required to transform the former into the latter are:

kitten → sitten (substitution of “s” for “k”)
sitten → sittin (substitution of “i” for “e”)
sittin → sitting (insertion of “g” at the end)

Quadratic Runtime, Linear Memory

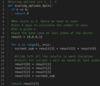
The iterative algorithm with two rows for strings s1 and s2 is as follows:

if s1 is equal to s2, return 0
Set m as length of s1
Set n as length of s2
if s1 is empty, return n
if s2 is empty, return m
create two arrays of integer distances d1[] and d2[] of length n+1
initialize d1 (previous row of distances) from 0..n
for each i from 0..m

calculate d2 (current row of distances) from the previous row d1 as follows:
d2[0] = i + 1
for each j from 0..n

if s1[i] is equal to s2[j], initialize cost to 0, otherwise initialize cost to 1
d2[j+1] = minimum( d2[j] +1, d1[j+1] + 1, d1[j] + cost )

copy d2 (current row) to d1 (previous row) for next iteration

return d2[n]

How well did you know this?

Not at all

Perfectly

0/1 Knapsack Problem

Given two integer arrays to represent weights and profits of ‘N’ items, we need to find a subset of these items which will give us maximum profit such that their cumulative weight is not more than a given number ‘C’. Each item can only be selected once, which means either we put an item in the knapsack or we skip it.

Let’s take the example of Merry, who wants to carry some fruits in the knapsack to get maximum profit. Here are the weights and profits of the fruits:

*Items:** { Apple, Orange, Banana, Melon }
*Weights:** { 2, 3, 1, 4 }
*Profits:** { 4, 5, 3, 7 }
*Knapsack capacity:** 5

Let’s try to put different combinations of fruits in the knapsack, such that their total weight is not more than 5:

Apple + Orange (total weight 5) => 9 profit
Apple + Banana (total weight 3) => 7 profit
Orange + Banana (total weight 4) => 8 profit
Banana + Melon (total weight 5) => 10 profit

This shows that Banana + Melon is the best combination, as it gives us the maximum profit and the total weight does not exceed the capacity.

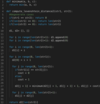
Dynamic Programming - 0/1 Knapsack-like - bottom-up DP solution. time and space complexity of O(N*C), where ‘N’ represents total items and ‘C’ is the maximum capacity.

Let’s try to populate our dp[][] array working in a bottom-up fashion. Essentially, we want to find the maximum profit for every sub-array and for every possible capacity. This means, dp[i][c] will represent the maximum knapsack profit for capacity c calculated from the first i items.

So, for each item at index i (0 <= i < items.length) and capacity c (0 <= c <= capacity), we have two options:

Exclude the item at index i. In this case, we will take whatever profit we get from the sub-array excluding this item => dp[i-1][c]
Include the item at index i; if its weight is not more than the capacity. In this case, we include its profit plus whatever profit we get from the remaining capacity and from remaining items => profit[i] + dp[i-1][c-weight[i]]

Finally, our optimal solution will be maximum of the above two values:

dp[i][c] = max (dp[i-1][c], profit[i] + dp[i-1][c-weight[i]])

How well did you know this?

Not at all

Perfectly

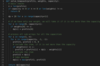
Equal Subset Sum Partition

Given a set of positive numbers, find if we can partition it into two subsets such that the sum of elements in both the subsets is equal.

Example 1
Input: {1, 2, 3, 4}

Output: True

Explanation: The given set can be partitioned into two subsets with equal sum: {1, 4} & {2, 3}

Example 2
Input: {2, 3, 4, 6}

Output: False

Explanation: The given set cannot be partitioned into two subsets with equal sum.

Dynamic Programming - 0/1 Knapsack-like

Let’s try to populate our dp[][] array from the above solution, working in a bottom-up fashion. Essentially, we want to find if we can make all possible sums with every subset. This means, dp[i][s] will be ‘true’ if we can make sum ‘s’ from the first ‘i’ numbers.

So, for each number at index ‘i’ (0 <= i < num.length) and sum ‘s’ (0 <= s <= S/2), we have two options:

Exclude the number. In this case, we will see if we can get ‘s’ from the subset excluding this number dp[i-1][s]
Include the number if its value is not more than ‘s’. In this case, we will see if we can find a subset to get the remaining sum dp[i-1][s-num[i]]

If either of the two above scenarios is true, we can find a subset of numbers with a sum equal to ‘s’.

The above solution has time and space complexity of O(N*S), where ‘N’ represents total numbers and ‘S’ is the total sum of all the numbers.

How well did you know this?

Not at all

Perfectly

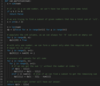
Subset Sum

Given a set of positive numbers, determine if there exists a subset whose sum is equal to a given number ‘S’.

Example 1
Input: {1, 2, 3, 7}, S=6

Output: True

The given set has a subset whose sum is ‘6’: {1, 2, 3}

Example 2
Input: {1, 2, 7, 1, 5}, S=10

Output: True

The given set has a subset whose sum is ‘10’: {1, 2, 7}

Example 3
Input: {1, 3, 4, 8}, S=6

Output: False

The given set does not have any subset whose sum is equal to ‘6’.

Dynamic Programming - 0/1 Knapsack-like. The solution has time and space complexity of O(N*S), where ‘N’ represents total numbers and ‘S’ is the required sum.

We’ll try to find if we can make all possible sums with every subset to populate the array dp[TotalNumbers][S+1].

For every possible sum ‘s’ (where 0 <= s <= S), we have two options:

Exclude the number. In this case, we will see if we can get the sum ‘s’ from the subset excluding this number => dp[index-1][s]
Include the number if its value is not more than ‘s’. In this case, we will see if we can find a subset to get the remaining sum => dp[index-1][s-num[index]]

If either of the above two scenarios returns true, we can find a subset with a sum equal to ‘s’.

How well did you know this?

Not at all

Perfectly

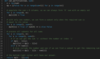
Minimum Subset Sum Difference

Given a set of positive numbers, partition the set into two subsets with a minimum difference between their subset sums.

Example 1
Input: {1, 2, 3, 9}
Output: 3
Explanation: We can partition the given set into two subsets where minimum absolute difference between the sum of numbers is ‘3’. Following are the two subsets: {1, 2, 3} & {9}.

Example 2
Input: {1, 2, 7, 1, 5}
Output: 0
Explanation: We can partition the given set into two subsets where minimum absolute difference between the sum of number is ‘0’. Following are the two subsets: {1, 2, 5} & {7, 1}.

Example 3
Input: {1, 3, 100, 4}
Output: 92
Explanation: We can partition the given set into two subsets where minimum absolute difference between the sum of numbers is ‘92’. Here are the two subsets: {1, 3, 4} & {100}.

Dynamic Programming - 0/1 Knapsack-like. time and space complexity of O(N*S), where ‘N’ represents total numbers and ‘S’ is the total sum of all the numbers.

Let’s assume ‘S’ represents the total sum of all the numbers. So what we are trying to achieve in this problem is to find a subset whose sum is as close to ‘S/2’ as possible, because if we can partition the given set into two subsets of an equal sum, we get the minimum difference i.e. zero. This transforms our problem to Subset Sum, where we try to find a subset whose sum is equal to a given number– ‘S/2’ in our case. If we can’t find such a subset, then we will take the subset which has the sum closest to ‘S/2’. This is easily possible, as we will be calculating all possible sums with every subset.

Essentially, we need to calculate all the possible sums up to ‘S/2’ for all numbers. So how do we populate the array db[TotalNumbers][S/2+1] in the bottom-up fashion?

For every possible sum ‘s’ (where 0 <= s <= S/2), we have two options:

Exclude the number. In this case, we will see if we can get the sum ‘s’ from the subset excluding this number =>dp[index-1][s]
Include the number if its value is not more than ‘s’. In this case, we will see if we can find a subset to get the remaining sum =>dp[index-1][s-num[index]]

If either of the two above scenarios is true, we can find a subset with a sum equal to ‘s’. We should dig into this before we can learn how to find the closest subset.

How well did you know this?

Not at all

Perfectly

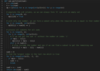
Count of Subset Sum

Given a set of positive numbers, find the total number of subsets whose sum is equal to a given number ‘S’.

Example 1
Input: {1, 1, 2, 3}, S=4
Output: 3
The given set has ‘3’ subsets whose sum is ‘4’: {1, 1, 2}, {1, 3}, {1, 3} Note that we have two similar sets {1, 3}, because we have two ‘1’ in our input.

Example 2
Input: {1, 2, 7, 1, 5}, S=9
Output: 3
The given set has ‘3’ subsets whose sum is ‘9’: {2, 7}, {1, 7, 1}, {1, 2, 1, 5}

Dynamic Programming - 0/1 Knapsack-like. Time and space complexity of O(N*S), where ‘N’ represents total numbers and ‘S’ is the desired sum.

We will try to find if we can make all possible sums with every subset to populate the array db[TotalNumbers][S+1].

So, at every step we have two options:

Exclude the number. Count all the subsets without the given number up to the given sum =>dp[index-1][sum]
Include the number if its value is not more than the ‘sum’. In this case, we will count all the subsets to get the remaining sum => dp[index-1][sum-num[index]]

To find the total sets, we will add both of the above two values:

dp[index][sum] = dp[index-1][sum] + dp[index-1][sum-num[index]])

How well did you know this?

Not at all

Perfectly

Target Sum

Given a set of positive numbers (non zero) and a target sum ‘S’. Each number should be assigned either a ‘+’ or ‘-’ sign. We need to find out total ways to assign symbols to make the sum of numbers equal to target ‘S’.

Example 1
Input: {1, 1, 2, 3}, S=1
Output: 3
Explanation: The given set has ‘3’ ways to make a sum of ‘1’: {+1-1-2+3} & {-1+1-2+3} & {+1+1+2-3}

Example 2
Input: {1, 2, 7, 1}, S=9
Output: 2
Explanation: The given set has ‘2’ ways to make a sum of ‘9’: {+1+2+7-1} & {-1+2+7+1}

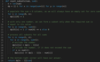
Dynamic Programming - 0/1 Knapsack-like. Time and space complexity of O(N*S), where ‘N’ represents total numbers and ‘S’ is the desired sum. We can further improve the solution to use only O(S) space.

We are asked to find two subsets of the given numbers whose difference is equal to the given target ‘S’. Take the first example above. As we saw, one solution is {+1-1-2+3}. So, the two subsets we are asked to find are {1, 3} & {1, 2} because,
(1 + 3) - (1 + 2) = 1
Now, let’s say ‘Sum(s1)’ denotes the total sum of set ‘s1’, and ‘Sum(s2)’ denotes the total sum of set ‘s2’. So the required equation is:
Sum(s1) - Sum(s2) = S
This equation can be reduced to the subset sum problem. Let’s assume that Sum(num) denotes the total sum of all the numbers, therefore:
Sum(s1) + Sum(s2) = Sum(num)
Let’s add the above tow equations:
=> Sum(s1) - Sum(s2) + Sum(s1) + Sum(s2) = S + Sum(num)

=> 2 * Sum(s1) = S + Sum(num)

=> Sum(s1) = (S + Sum(num)) / 2
This essentially converts our problem to: “Find count of subsets of the given numbers whose sum is equal to”,
=> (S + Sum(num)) / 2
Here is the code for the space-optimized solution, using only a single array:

How well did you know this?

Not at all

Perfectly

Unbounded Knapsack

Given the weights and profits of ‘N’ items, we are asked to put these items in a knapsack which has a capacity ‘C’. The goal is to get the maximum profit from the items in the knapsack. The only difference between the 0/1 Knapsack problem and this problem is that we are allowed to use an unlimited quantity of an item.

Let’s take the example of Merry, who wants to carry some fruits in the knapsack to get maximum profit. Here are the weights and profits of the fruits:

*Items:** { Apple, Orange, Melon }
*Weights:** { 1, 2, 3 }
*Profits:** { 15, 20, 50 }
*Knapsack capacity:** 5

Let’s try to put different combinations of fruits in the knapsack, such that their total weight is not more than 5.

5 Apples (total weight 5) =\> 75 profit
1 Apple + 2 Oranges (total weight 5) =\> 55 profit
2 Apples + 1 Melon (total weight 5) =\> 80 profit
1 Orange + 1 Melon (total weight 5) =\> 70 profit

This shows that 2 apples + 1 melon is the best combination, as it gives us the maximum profit and the total weight does not exceed the capacity.

Dynamic Programming - Unbounded Knapsack-like. time and space complexity of O(N*C), where ‘N’ represents total items and ‘C’ is the maximum capacity.

Let’s try to populate our dp[][] array from the above solution, working in a bottom-up fashion. Essentially, what we want to achieve is: “Find the maximum profit for every sub-array and for every possible capacity”.

So for every possible capacity ‘c’ (0 <= c <= capacity), we have two options:

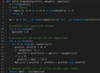
Exclude the item. In this case, we will take whatever profit we get from the sub-array excluding this item:dp[index-1][c]
Include the item if its weight is not more than the ‘c’. In this case, we include its profit plus whatever profit we get from the remaining capacity: profit[index] + dp[index][c-weight[index]]
Finally, we have to take the maximum of the above two values:
dp[index][c] = max (dp[index-1][c], profit[index] + dp[index][c-weight[index]])

How well did you know this?

Not at all

Perfectly

Rod Cutting

Given a rod of length ‘n’, we are asked to cut the rod and sell the pieces in a way that will maximize the profit. We are also given the price of every piece of length ‘i’ where ‘1 <= i <= n’.

Example

*Lengths:** [1, 2, 3, 4, 5]
*Prices:** [2, 6, 7, 10, 13]
*Rod Length:** 5

Let’s try different combinations of cutting the rod:

Five pieces of length 1 => 10 price
Two pieces of length 2 and one piece of length 1 => 14 price
One piece of length 3 and two pieces of length 1 => 11 price
One piece of length 3 and one piece of length 2 => 13 price
One piece of length 4 and one piece of length 1 => 12 price
One piece of length 5 => 13 price

This shows that we get the maximum price (14) by cutting the rod into two pieces of length ‘2’ and one piece of length ‘1’.

Dynamic Programming - Unbounded Knapsack-like. time and space complexity of O(N*C), where ‘N’ represents total items and ‘C’ is the maximum capacity.

Let’s try to populate our dp[][] array in a bottom-up fashion. Essentially, what we want to achieve is: “Find the maximum sales price for every rod length and for every possible sales price”.

So for every possible rod length ‘len’ (0<= len <= n), we have two options:

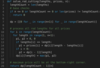
Exclude the piece. In this case, we will take whatever price we get from the rod length excluding this piece => dp[index-1][len]
Include the piece if its length is not more than ‘len’. In this case, we include its price plus whatever price we get from the remaining rod length => prices[index] + dp[index][len-lengths[index]]

Finally, we have to take the maximum of the above two values:
dp[index][len] = max (dp[index-1][len], prices[index] + dp[index][len-lengths[index]])

How well did you know this?

Not at all

Perfectly

Coin Change

Given an infinite supply of ‘n’ coin denominations and a total money amount, we are asked to find the total number of distinct ways to make up that amount.

Example

Denominations: {1,2,3}

Total amount: 5

Output: 5

Explanation: There are five ways to make the change for ‘5’, here are those ways:

{1,1,1,1,1}
{1,1,1,2}
{1,2,2}
{1,1,3}
{2,3}

Dynamic Programming - Unbounded Knapsack-like. Time and space complexity of O(C*T), where ‘C’ represents total coin denominations and ‘T’ is the total amount that we want to make change.

We will try to find if we can make all possible sums, with every combination of coins, to populate the array dp[TotalDenominations][Total+1].

So for every possible total ‘t’ (0<= t <= Total) and for every possible coin index (0 <= index < denominations.length), we have two options:

Exclude the coin. Count all the coin combinations without the given coin up to the total ‘t’ =>dp[index-1][t]
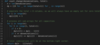
Include the coin if its value is not more than ‘t’. In this case, we will count all the coin combinations to get the remaining total: dp[index][t-denominations[index]]

Finally, to find the total combinations, we will add both the above two values:

` dp[index][t] = dp[index-1][t] + dp[index][t-denominations[index]`

How well did you know this?

Not at all

Perfectly

Minimum Coin Change

Given an infinite supply of ‘n’ coin denominations and a total money amount, we are asked to find the minimum number of coins needed to make up that amount.

Example 1
Denominations: {1,2,3}
Total amount: 5
Output: 2
Explanation: We need minimum of two coins {2,3} to make a total of ‘5’

Example 2
Denominations: {1,2,3}
Total amount: 11
Output: 4
Explanation: We need minimum four coins {2,3,3,3} to make a total of ‘11’

Dynamic Programming - Unbounded Knapsack-like. Time and space complexity of O(C*T), where ‘C’ represents total coin denominations and ‘T’ is the total amount that we want to make change.

Let’s try to populate our array dp[TotalDenominations][Total+1] for every possible total with a minimum number of coins needed.

So for every possible total ‘t’ (0<= t <= Total) and for every possible coin index (0 <= index < denominations.length), we have two options:

Exclude the coin: In this case, we will take the minimum coin count from the previous set =>dp[index-1][t]
Include the coin if its value is not more than ‘t’: In this case, we will take the minimum count needed to get the remaining total, plus include ‘1’ for the current coin =>dp[index][t-denominations[index]] + 1

Finally, we will take the minimum of the above two values for our solution:

` dp[index][t] = min(dp[index-1][t], dp[index][t-denominations[index] + 1)`

How well did you know this?

Not at all

Perfectly

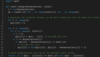
Maximum Ribbon Cut

We are given a ribbon of length ‘n’ and a set of possible ribbon lengths. Now we need to cut the ribbon into the maximum number of pieces that comply with the above-mentioned possible lengths. Write a method that will return the count of pieces.

Example 1
n: 5
Ribbon Lengths: {2,3,5}
Output: 2
Explanation: Ribbon pieces will be {2,3}.

Example 2
n: 7
Ribbon Lengths: {2,3}
Output: 3
Explanation: Ribbon pieces will be {2,2,3}.

Example 3
n: 13
Ribbon Lengths: {3,5,7}
Output: 3
Explanation: Ribbon pieces will be {3,3,7}.

Dynamic Programming - Unbounded Knapsack-like. Time and space complexity of O(L*N), where ‘L’ represents total ribbon lengths and ‘N’ is the total length that we want to cut.

Since this problem is quite similar to Minimum Coin Change, let’s jump on to the bottom-up dynamic programming solution.

Let’s try to populate our array dp[ribbonLength][total+1] for every possible ribbon length with a maximum number of pieces.

So for every possible length ‘len’ (0<= len <= total) and for every possible ribbon length index (0 <= index < ribbonLengths.length), we have two options:

Exclude the ribbon length: In this case, we will take the maximum pieces count from the previous set =>dp[index-1][len]
Include the ribbon length if its value is not more than ‘len’: In this case, we will take the maximum pieces needed to get the remaining total, plus include ‘1’ for the current ribbon length =>1 + dp[index][len-ribbonLengths[index]]

Finally, we will take the maximum of the above two values for our solution:

dp[index][t] = max(dp[index-1][len], 1 + dp[index][len-denominations[index])

How well did you know this?

Not at all

Perfectly

Fibonacci numbers

Write a function to calculate the nth Fibonacci number.

Fibonacci numbers are a series of numbers in which each number is the sum of the two preceding numbers. First few Fibonacci numbers are: 0, 1, 1, 2, 3, 5, 8, …

Mathematically we can define the Fibonacci numbers as:

Fib(n) = Fib(n-1) + Fib(n-2), for n > 1

Given that: Fib(0) = 0, and Fib(1) = 1

Dynamic Programming - Fibonacci numbers-like. Time and space complexity of O(n)

Let’s try to populate our dp[] array, working in a bottom-up fashion. Since every Fibonacci number is the sum of the previous two numbers, we can use this fact to populate our array.

Staircase

Given a stair with ‘n’ steps, implement a method to count how many possible ways are there to reach the top of the staircase, given that, at every step you can either take 1 step, 2 steps, or 3 steps.

Example 1
Number of stairs (n): 3
Number of ways: 4
Explanation: Following are the four ways we can climb : {1,1,1}, {1,2}, {2,1}, {3}

Example 2
Number of stairs (n): 4
Number of ways: 7
Explanation: Following are the seven ways we can climb : {1,1,1,1}, {1,1,2}, {1,2,1}, {2,1,1}, {2,2}, {1,3}, {3,1}

Dynamic Programming - Fibonacci numbers-like. Linear runtime. Linear or constant memory.

Let’s try to populate our dp[] array from the above solution, working in a bottom-up fashion. As we saw in the above code, every CountWaysRecursive(n) is the sum of the previous three counts. We can use this fact to populate our array.

We can optimize the space used in our previous solution. We don’t need to store all the counts up to ‘n’, as we only need three previous numbers to calculate the next count.

Number factors

Given a number ‘n’, implement a method to count how many possible ways there are to express ‘n’ as the sum of 1, 3, or 4.

Example 1

n: 4

Number of ways: 4

Explanation: Following are the four ways we can exoress ‘n’ : {1,1,1,1}, {1,3}, {3,1}, {4}

Example 2

n: 5

Number of ways: 6

Explanation: Following are the six ways we can express ‘n’ : {1,1,1,1,1}, {1,1,3}, {1,3,1}, {3,1,1}, {1,4}, {4,1}

Dynamic Programming - Fibonacci numbers-like. Time and space complexity of O(n).

Let’s try to populate our dp[] array from the above solution, working in a bottom-up fashion. As we saw in the above code, every CountWaysRecursive(n) is the sum of the three counts. We can use this fact to populate our array.

We can clearly see that this problem follows the Fibonacci number pattern. However, every number in a Fibonacci series is the sum of the previous two numbers, whereas in this problem every count is a sum of previous three numbers: previous-1, previous-3, and previous-4.

Minimum jumps to reach the end

Given an array of positive numbers, where each element represents the max number of jumps that can be made forward from that element, write a program to find the minimum number of jumps needed to reach the end of the array (starting from the first element). If an element is 0, then we cannot move through that element.

Example 1
Input: {2,1,1,1,4}
Output: 3
Explanation: Starting from index ‘0’, we can reach the last index through: 0->2->3->4

Example 2
Input: {1,1,3,6,9,3,0,1,3}
Output: 4
Explanation: Starting from index ‘0’, we can reach the last index through: 0->1->2->3->8

Dynamic Programming - Fibonacci numbers-like. time complexity of O(n²) (because of the two for loops) and space complexity of O(n) to store dp[].

Let’s try to populate our dp[] array from the above solution, working in the bottom-up fashion. As we saw in the above code, we were trying to find the minimum jumps needed to reach every index (if it is within the range) from the current index. We can use this fact to populate our array.

As we know, every index within the range of current index can be reached in one jump. Therefore, we can say that we can reach every index (within the range of current index) in:
'jumps to reach current index' + 1

So, while going through all the indexes, we will take the minimum value between the current jump-count and the jumps needed to reach the current index + 1.

Minimum jumps with fee

Given a staircase with n steps and an array of n numbers representing the fee that you have to pay if you take the step. Implement a method to calculate the minimum fee required to reach the top of the staircase. At every step, you have an option to take either 1 step, 2 steps, or 3 steps. You should assume that you are standing at the first step.

Example 1
Number of stairs (n): 6
Fee: {1,2,5,2,1,2}
Output: 3
Explanation: Starting from index ‘0’, we can reach the top through: 0->3->top The total fee we have to pay will be (1+2).

Example 2
Number of stairs (n): 4
Fee: {2,3,4,5}
Output: 5
Explanation: Starting from index ‘0’, we can reach the top through: 0->1->top The total fee we have to pay will be (2+3).

Dynamic Programming - Fibonacci numbers-like. Time and space complexity of O(n).

Let’s try to populate our dp[] array from the above solution, working in a bottom-up fashion. As we saw in the above code, every findMinFeeRecursive(n) is the minimum of the three recursive calls; we can use this fact to populate our array.

We can clearly see that this problem follows the Fibonacci number pattern. The only difference is that every Fibonacci number is a sum of the two preceding numbers, whereas in this problem every number (total fee) is the minimum of previous three numbers.

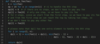
House thief

Given a number array representing the wealth of n houses, determine the maximum amount of money the thief can steal without alerting the security system.

Example 1
Input: {2, 5, 1, 3, 6, 2, 4}
Output: 15
Explanation: The thief should steal from houses 5 + 6 + 4

Example 2
Input: {2, 10, 14, 8, 1}
Output: 18
Explanation: The thief should steal from houses 10 + 8

Dynamic Programming - Fibonacci numbers-like. time and space complexity of O(n)

Let’s try to populate our dp[] array from the above solution, working in a bottom-up fashion. As we saw in the above code, every findMaxStealRecursive() is the maximum of the two recursive calls; we can use this fact to populate our array.

We don’t need to store all the previous numbers up to ‘n’, as we only need two previous numbers to calculate the next number in the sequence. Let’s use this fact to further improve our solution.

Longest Palindromic Subsequence

Given a sequence, find the length of its Longest Palindromic Subsequence (LPS). In a palindromic subsequence, elements read the same backward and forward.

A subsequence is a sequence that can be derived from another sequence by deleting some or no elements without changing the order of the remaining elements.

Example 1
Input: “abdbca”
Output: 5
Explanation: LPS is “abdba”

Example 2
Input: “cddpd”
Output: 3
Explanation: LPS is “ddd”

Example 3
Input: “pqr”
Output: 1
Explanation: LPS could be “p”, “q” or “r”

Dynamic Programming - Longest Palindromic Subsequence-like. Time and space complexity of the above algorithm is O(n²), where ‘n’ is the length of the input sequence.

Since we want to try all the subsequences of the given sequence, we can use a two-dimensional array to store our results. We can start from the beginning of the sequence and keep adding one element at a time. At every step, we will try all of its subsequences. So for every startIndex and endIndex in the given string, we will choose one of the following two options:

If the element at the startIndex matches the element at the endIndex, the length of LPS would be two plus the length of LPS till startIndex+1 and endIndex-1.
If the element at the startIndex does not match the element at the endIndex, we will take the maximum LPS created by either skipping element at the startIndex or the endIndex.

So our recursive formula would be:
if st[endIndex] == st[startIndex]
dp[startIndex][endIndex] = 2 + dp[startIndex + 1][endIndex - 1]
else
dp[startIndex][endIndex] = Math.max(dp[startIndex + 1][endIndex], dp[startIndex][endIndex - 1])

Longest Palindromic Substring

Given two strings ‘s1’ and ‘s2’, find the length of the longest substring which is common in both the strings.

Example 1
Input: s1 = “abdca” s2 = “cbda”
Output: 2
Explanation: The longest common substring is “bd”.

Example 2
Input: s1 = “passport” s2 = “ppsspt”
Output: 3
Explanation: The longest common substring is “ssp”.

Dynamic Programming - Longest Palindromic Subsequence-like. Time and space complexity of the above algorithm is O(n²), where ‘n’ is the length of the input string.

Since we want to try all the substrings of the given string, we can use a two-dimensional array to store the subproblems’ results. So dp[i][j] will be ‘true’ if the substring from index ‘i’ to index ‘j’ is a palindrome.

We can start from the beginning of the string and keep adding one element at a time. At every step, we will try all of its substrings. So for every endIndex and startIndex in the given string, we need to check the following thing:

If the element at the startIndex matches the element at the endIndex, we will further check if the remaining substring (from startIndex+1 to endIndex-1) is a substring too.

So our recursive formula will look like:

if st[startIndex] == st[endIndex], and

if the remaing string is of zero length or dp[startIndex+1][endIndex-1] is a palindrome then
dp[startIndex][endIndex] = true

Count of Palindromic Substrings

Given a string, find the total number of palindromic substrings in it. Please note we need to find the total number of substrings and not subsequences.

Example 1
Input: “abdbca”
Output: 7
Explanation: Here are the palindromic substrings, “a”, “b”, “d”, “b”, “c”, “a”, “bdb”.

Example 2
Input: = “cddpd”
Output: 7
Explanation: Here are the palindromic substrings, “c”, “d”, “d”, “p”, “d”, “dd”, “dpd”.

Example 3
Input: = “pqr”
Output: 3
Explanation: Here are the palindromic substrings,”p”, “q”, “r”.

Dynamic Programming - Longest Palindromic Subsequence-like

This problem follows the Longest Palindromic Subsequence pattern, and can be easily converted to Longest Palindromic Substring. The only difference is that instead of calculating the longest palindromic substring, we will instead count all the palindromic substrings.

Let’s jump directly to the bottom-up dynamic programming solution

The time and space complexity of the algorithm is O(n²), where ‘n’ is the length of the input string.

Minimum Deletions in a String to make it a Palindrome

Given a string, find the minimum number of characters that we can remove to make it a palindrome.

Example 1
Input: “abdbca”
Output: 1
Explanation: By removing “c”, we get a palindrome “abdba”.

Example 2
Input: = “cddpd”
Output: 2
Explanation: Deleting “cp”, we get a palindrome “ddd”.

Example 3
Input: = “pqr”
Output: 2
Explanation: We have to remove any two characters to get a palindrome, e.g. if we remove “pq”, we get palindrome “r”.

Dynamic Programming - Longest Palindromic Subsequence-like

This problem can be easily converted to the Longest Palindromic Subsequence (LPS) problem. We can use the fact that LPS is the best subsequence we can have, so any character that is not part of LPS must be removed. Please note that it is ‘Longest Palindromic SubSequence’ and not ‘Longest Palindrome Substring’.

So, our solution for a given string ‘st’ will be:
Minimum_deletions_to_make_palindrome = Length(st) - LPS(st)

The time and space complexity of the above algorithm is O(n2), where ‘n’ is the length of the input string.

Palindromic Partitioning

Given a string, we want to cut it into pieces such that each piece is a palindrome. Write a function to return the minimum number of cuts needed.

Example 1
Input: “abdbca”

Output: 3

Explanation: Palindrome pieces are “a”, “bdb”, “c”, “a”.

Example 2
Input: = “cddpd”

Output: 2

Explanation: Palindrome pieces are “c”, “d”, “dpd”.

Example 3
Input: = “pqr”

Output: 2

Explanation: Palindrome pieces are “p”, “q”, “r”.

Example 4
Input: = “pp”

Output: 0

Explanation: We do not need to cut, as “pp” is a palindrome.

Dynamic Programming - Longest Palindromic Subsequence-like

We need to build two tables, one for the isPalindrome() and one for finding the minimum cuts needed.

If you remember, we built a table in the Longest Palindromic Substring (LPS) chapter that can tell us what substrings (of the input string) are palindrome. We will use the same approach here to build the table required for isPalindrome(). For example, here is the final output from LPS for “cddpd”.

To build the second table for finding the minimum cuts, we can iterate through the first table built for isPalindrome(). At any step, if we get a palindrome, we can cut the string there. Which means minimum cuts will be one plus the cuts needed for the remaining string.

The time and space complexity of the above algorithm is O(n²), where ‘n’ is the length of the input string.

Longest Common Substring

Given two strings ‘s1’ and ‘s2’, find the length of the longest substring which is common in both the strings.

Example 1
Input: s1 = “abdca” s2 = “cbda”
Output: 2
Explanation: The longest common substring is “bd”.

Example 2
Input: s1 = “passport” s2 = “ppsspt”
Output: 3
Explanation: The longest common substring is “ssp”.

Dynamic Programming - Substring-like

Since we want to match all the substrings of the given two strings, we can use a two-dimensional array to store our results. The lengths of the two strings will define the size of the two dimensions of the array. So for every index i in string s1 and j in string s2, we have two options:

If the character at s1[i] matches s2[j], the length of the common substring would be one plus the length of the common substring till i-1 and j-1 indexes in the two strings.
If the character at the s1[i] does not match s2[j], we don’t have any common substring.

The time and space complexity of the above algorithm is O(m*n), where ‘m’ and ‘n’ are the lengths of the two input strings.

Longest Common Subsequence

Given two strings ‘s1’ and ‘s2’, find the length of the longest subsequence which is common in both the strings.

A subsequence is a sequence that can be derived from another sequence by deleting some or no elements without changing the order of the remaining elements.

Example 1
Input: s1 = “abdca” s2 = “cbda”
Output: 3
Explanation: The longest common subsequence is “bda”.

Example 2
Input: s1 = “passport” s2 = “ppsspt”
Output: 5
Explanation: The longest common subsequence is “psspt”.

Dynamic Programming - Substring-like. Time and space complexity of the above algorithm is O(m*n), where ‘m’ and ‘n’ are the lengths of the two input strings.

Since we want to match all the subsequences of the given two strings, we can use a two-dimensional array to store our results. The lengths of the two strings will define the size of the array’s two dimensions. So for every index i in string s1 and j in string s2, we will choose one of the following two options:

If the character s1[i] matches s2[j], the length of the common subsequence would be one plus the length of the common subsequence till the i-1 and j-1 indexes in the two respective strings.
If the character s1[i] does not match s2[j], we will take the longest subsequence by either skipping ith or jth character from the respective strings.

So our recursive formula would be:

if s1[i] == s2[j]

` dp[i][j] = 1 + dp[i-1][j-1]`

else

` dp[i][j] = max(dp[i-1][j], dp[i][j-1])`

Minimum Deletions and Insertions to Transform a String into another

Given strings s1 and s2, we need to transform s1 into s2 by deleting and inserting characters. Write a function to calculate the count of the minimum number of deletion and insertion operations.

Example 1
Input: s1 = “abc” s2 = “fbc”
Output: 1 deletion and 1 insertion.
Explanation: We need to delete {‘a’} and insert {‘f’} to s1 to transform it into s2.

Example 2
Input: s1 = “abdca” s2 = “cbda”
Output: 2 deletions and 1 insertion.
Explanation: We need to delete {‘a’, ‘c’} and insert {‘c’} to s1 to transform it into s2.

Example 3
Input: s1 = “passport” s2 = “ppsspt”
Output: 3 deletions and 1 insertion
Explanation: We need to delete {‘a’, ‘o’, ‘r’} and insert {‘p’} to s1 to transform it into s2.

Dynamic Programming - Substring-like. Time and space complexity of the above algorithm is O(m*n), where ‘m’ and ‘n’ are the lengths of the two input strings.

This problem can easily be converted to the Longest Common Subsequence (LCS). If we can find the LCS of the two input strings, we can easily find how many characters we need to insert and delete from s1. Here is how we can do this:

Let’s assume len1 is the length of s1 and len2 is the length of s2.
Now let’s assume c1 is the length of LCS of the two strings s1 and s2.
To transform s1 into s2, we need to delete everything from s1 which is not part of LCS, so minimum deletions we need to perform from s1 =>len1 - c1
Similarly, we need to insert everything in s1 which is present in s2 but not part of LCS, so minimum insertions we need to perform in s1 =>len2 - c1

Let’s jump directly to the bottom-up dynamic programming solution

Longest Increasing Subsequence

Given a number sequence, find the length of its Longest Increasing Subsequence (LIS). In an increasing subsequence, all the elements are in increasing order (from lowest to highest).

Example 1
Input: {4,2,3,6,10,1,12}
Output: 5
Explanation: The LIS is {2,3,6,10,12}.

Example 2
Input: {-4,10,3,7,15}
Output: 4
Explanation: The LIS is {-4,3,7,15}.

Dynamic Programming - Substring-like. The time complexity of the above algorithm is O(n²) and the space complexity is O(n).

The above algorithm tells us two things:

If the number at the current index is bigger than the number at the previous index, we increment the count for LIS up to the current index.
But if there is a bigger LIS without including the number at the current index, we take that.

So we need to find all the increasing subsequences for the number at index i, from all the previous numbers (i.e. number till index i-1), to eventually find the longest increasing subsequence.

If i represents the currentIndex and j represents the previousIndex, our recursive formula would look like:

` if num[i] > num[j] => dp[i] = dp[j] + 1 if there is no bigger LIS for ‘i’`

Maximum Sum Increasing Subsequence

Given a number sequence, find the increasing subsequence with the highest sum. Write a method that returns the highest sum.

Example 1
Input: {4,1,2,6,10,1,12}
Output: 32
Explanation: The increaseing sequence is {4,6,10,12}. Please note the difference, as the LIS is {1,2,6,10,12} which has a sum of ‘31’.

Example 2
Input: {-4,10,3,7,15}
Output: 25
Explanation: The increaseing sequences are {10, 15} and {3,7,15}.

Dynamic Programming - Substring-like. The time complexity of the above algorithm is O(n²) and the space complexity is O(n).

The above algorithm tells us two things:

If the number at the current index is bigger than the number at the previous index, we include that number in the sum for an increasing sequence up to the current index.
But if there is a maximum sum increasing subsequence (MSIS), without including the number at the current index, we take that.

So we need to find all the increasing subsequences for a number at index i, from all the previous numbers (i.e. numbers till index i-1), to find MSIS.

If i represents the currentIndex and j represents the previousIndex, our recursive formula would look like:

` if num[i] > num[j] => dp[i] = dp[j] + num[i] if there is no bigger MSIS for ‘i’`

Shortest Common Super-sequence

Given two sequences ‘s1’ and ‘s2’, write a method to find the length of the shortest sequence which has ‘s1’ and ‘s2’ as subsequences.

Example 1
Input: s1: “abcf” s2:”bdcf”
Output: 5
Explanation: The shortest common super-sequence (SCS) is “abdcf”.

Example 2
Input: s1: “dynamic” s2:”programming”
Output: 15
Explanation: The SCS is “dynprogrammicng”.

Dynamic Programming - Substring-like. The time and space complexity of the above algorithm is O(n*m).

Since we want to match all the subsequences of the given sequences, we can use a two-dimensional array to store our results. The lengths of the two strings will define the size of the array’s dimensions. So for every index i in sequence s1 and j in sequence s2, we will choose one of the following two options:

If the character s1[i] matches s2[j], the length of the SCS would be the one plus the length of the SCS till i-1 and j-1 indexes in the two strings.
If the character s1[i] does not match s2[j], we will consider two SCS: one without s1[i] and one without s2[j]. Our required SCS length will be the shortest of these two super-sequences plus one.

So our recursive formula would be:

if s1[i] == s2[j]

` dp[i][j] = 1 + dp[i-1][j-1]`

else

` dp[i][j] = 1 + min(dp[i-1][j], dp[i][j-1]) `

Minimum Deletions to Make a Sequence Sorted

Given a number sequence, find the minimum number of elements that should be deleted to make the remaining sequence sorted.

Example 1
Input: {4,2,3,6,10,1,12}
Output: 2
Explanation: We need to delete {4,1} to make the remaing sequence sorted {2,3,6,10,12}.

Example 2
Input: {-4,10,3,7,15}
Output: 1
Explanation: We need to delete {10} to make the remaing sequence sorted {-4,3,7,15}.

Example 3
Input: {3,2,1,0}
Output: 3
Explanation: Since the elements are in reverse order, we have to delete all except one to get a sorted sequence. Sorted sequences are {3}, {2}, {1}, and {0}

Dynamic Programming - Substring-like. The time complexity of the above algorithm is O(n²) and the space complexity is O(n).

we can convert this problem into a Longest Increasing Subsequence (LIS) problem. As we know that LIS will give us the length of the longest increasing subsequence (in the sorted order!), which means that the elements which are not part of the LIS should be removed to make the sequence sorted. This is exactly what we need. So we’ll get our solution by subtracting the length of LIS from the length of the input array: Length-of-input-array - LIS()

Longest Repeating Subsequence

Given a sequence, find the length of its longest repeating subsequence (LRS). A repeating subsequence will be the one that appears at least twice in the original sequence and is not overlapping (i.e. none of the corresponding characters in the repeating subsequences have the same index).

Example 1

Input: “t o m o r r o w”

Output: 2

Explanation: The longest repeating subsequence is “or” {tomorrow}.

Example 2

Input: “a a b d b c e c”

Output: 3

Explanation: The longest repeating subsequence is “a b c” {a a b d b c e c}.

Example 3

Input: “f m f f”

Output: 2

Explanation: The longest repeating subsequence is “f f” {f m f f, f m f f}. Please note the second last character is shared in LRS.

Dynamic Programming - Substring-like. The time and space complexity of the above algorithm is O(n²), where ‘n’ is the length of the input sequence.

Since we want to match all the subsequences of the given string, we can use a two-dimensional array to store our results. As mentioned above, we will be tracking two indexes to overcome the overlapping problem. So for each of the two indexes, i1 and i2, we will choose one of the following options:

If ‘i1’ and ‘i2’ are different and the character str[i1] matches the character str[i2], then the length of the LRS would be one plus the length of LRS up to i1-1 and i2-1 indexes.
If the character at str[i1] does not match str[i2], we will take the LRS by either skipping i1th or i2th character.

So our recursive formula would be:

if i1 != i2 && str[i1] == str[i2]

` dp[i1][i2] = 1 + dp[i1-1][i2-1]`

else

` dp[i1][i2] = max(dp[i1-1][i2], dp[i1][i2-1])`

Subsequence Pattern Matching

Given a string and a pattern, write a method to count the number of times the pattern appears in the string as a subsequence.

Example 1
Input: string: “baxmx”, patten: “ax”
Output: 2
Explanation: {baxmx, baxmx}.

Example 2
Input: string: “tomorrow”, pattern: “tor”
Output: 4
Explanation: Following are the four occurences: {tomorrow, tomorrow, tomorrow, tomorrow}.

Dynamic Programming - Substring-like. The time and space complexity of the above algorithm is O(m*n), where ‘m’ and ‘n’ are the lengths of the string and the pattern respectively.

Since we want to match all the subsequences of the given string, we can use a two-dimensional array to store our results. As mentioned above, we will be tracking separate indexes for the string and the pattern, so we will be doing two things for every value of strIndex and patIndex:

If the character at the strIndex (in the string) matches the character at patIndex (in the pattern), the count of the SPM would be equal to the count of SPM up to strIndex-1 and patIndex-1.
At every step, we can always skip a character from the string to try matching the remaining string with the pattern; therefore, we can add the SPM count from the indexes strIndex-1 and patIndex.

So our recursive formula would be:

if str[strIndex] == pat[patIndex] {

` dp[strIndex][patIndex] = dp[strIndex-1][patIndex-1]`

}

dp[i1][i2] += dp[strIndex-1][patIndex]

Longest Bitonic Subsequence

Given a number sequence, find the length of its Longest Bitonic Subsequence (LBS). A subsequence is considered bitonic if it is monotonically increasing and then monotonically decreasing.

Example 1

Input: {4,2,3,6,10,1,12}

Output: 5

Explanation: The LBS is {2,3,6,10,1}.

Example 2

Input: {4,2,5,9,7,6,10,3,1}

Output: 7

Explanation: The LBS is {4,5,9,7,6,3,1}.

Dynamic Programming - Substring-like. The time complexity of the algorithm is O(n²) and the space complexity is O(n).

The algorithm shows us a clear bottom-up approach. We can separately calculate LDS for every index i.e., from the beginning to the end of the array and vice versa. The required length of MBS would be the one that has the maximum sum of LDS for a given index (from both the ends).

Longest Alternating Subsequence

Given a number sequence, find the length of its Longest Alternating Subsequence (LAS). A subsequence is considered alternating if its elements are in alternating order.

A three element sequence (a1, a2, a3) will be an alternating sequence if its elements hold one of the following conditions:

{a1 > a2 a3}

Example 1
Input: {1,2,3,4}
Output: 2
Explanation: There are many LAS: {1,2}, {3,4}, {1,3}, {1,4}

Example 2
Input: {3,2,1,4}
Output: 3
Explanation: The LAS are {3,2,4} and {2,1,4}.

Example 3
Input: {1,3,2,4}
Output: 4
Explanation: The LAS is {1,3,2,4}.

Dynamic Programming - Substring-like. The time complexity of the algorithm is O(n²) and the space complexity is O(n).

The algorithm tells us three things:

We need to find an ascending and descending subsequence at every index.
While finding the next element in the ascending order, if the number at the current index is bigger than the number at the previous index, we increment the count for a LAS up to the current index. But if there is a bigger LAS without including the number at the current index, we take that.
Similarly for the descending order, if the number at the current index is smaller than the number at the previous index, we increment the count for a LAS up to the current index. But if there is a bigger LAS without including the number at the current index, we take that.

To find the largest LAS, we need to find all of the LAS for a number at index i from all the previous numbers (i.e. number till index i-1).

We can use two arrays to store the length of LAS, one for ascending order and one for descending order. (Actually, we will use a two-dimensional array, where the second dimension will be of size two).

If i represents the currentIndex and j represents the previousIndex, our recursive formula would look like:

If nums[i] is bigger than nums[j] then we will consider the LAS ending at j where the last two elements were in descending order =>

if num[i] > num[j] => dp[i][0] = 1 + dp[j][1], if there is no bigger LAS for 'i'

If nums[i] is smaller than nums[j] then we will consider the LAS ending at j where the last two elements were in ascending order =>

if num[i] dp[i][1] = 1 + dp[j][0], if there is no bigger LAS for 'i'

Edit Distance

Given strings s1 and s2, we need to transform s1 into s2 by deleting, inserting, or replacing characters. Write a function to calculate the count of the minimum number of edit operations.

Example 1
Input: s1 = “bat” s2 = “but”
Output: 1
Explanation: We just need to replace ‘a’ with ‘u’ to transform s1 to s2.

Example 2
Input: s1 = “abdca” s2 = “cbda”
Output: 2
Explanation: We can replace first ‘a’ with ‘c’ and delete second ‘c’.

Example 3
Input: s1 = “passpot” s2 = “ppsspqrt”
Output: 3
Explanation: Replace ‘a’ with ‘p’, ‘o’ with ‘q’, and insert ‘r’.

Dynamic Programming - Substring-like. The time and space complexity of the algorithm is O(n*m) where ‘m’ and ‘n’ are the lengths of the two input strings.

Since we want to match all the characters of the given two strings, we can use a two-dimensional array to store our results. The lengths of the two strings will define the size of the two dimensions of the array. So for every index i1 in string s1 and i2 in string s2, we will choose one of the following options:

If the character s1[i1] matches s2[i2], the count of the edit operations will be equal to the count of the edit operations for the remaining strings.
If the character s1[i1] does not match s2[i2], we will take the minimum count from the remaining strings after performing any of the three edit operations.

So our recursive formula would be:

if s1[i1] == s2[i2]

` dp[i1][i2] = dp[i1-1][i2-1]`

else

` dp[i1][i2] = 1 + min(dp[i1-1][i2], // delete`

` dp[i1][i2-1], // insert `

` dp[i1-1][i2-1]) // replace`

Strings Interleaving

Give three strings ‘m’, ‘n’, and ‘p’, write a method to find out if ‘p’ has been formed by interleaving ‘m’ and ‘n’. ‘p’ would be considered interleaving ‘m’ and ‘n’ if it contains all the letters from ‘m’ and ‘n’ and the order of letters is preserved too.

Example 1
Input: m=”abd”, n=”cef”, p=”abcdef”
Output: true
Explanation: ‘p’ contains all the letters from ‘m’ and ‘n’ and preserves their order too.

Example 2
Input: m=”abd”, n=”cef”, p=”adcbef”
Output: false
Explanation: ‘p’ contains all the letters from ‘m’ and ‘n’ but does not preserve the order.

Example 3
Input: m=”abc”, n=”def”, p=”abdccf”
Output: false
Explanation: ‘p’ does not contain all the letters from ‘m’ and ‘n’.

Example 4
Input: m=”abcdef”, n=”mnop”, p=”mnaobcdepf”
Output: true
Explanation: ‘p’ contains all the letters from ‘m’ and ‘n’ and preserves their order too.

Dynamic Programming - Substring-like. The time and space complexity of the above algorithm is O(m*n), where m and n are the lengths of the two interleaving strings.

Since we want to completely match m and n (the two interleaving strings) with p, we can use a two-dimensional array to store our results. The lengths of m and n will define the dimensions of the result array.

As mentioned above, we will be tracking separate indexes for m, n and p, so we will have the following options for every value of mIndex, nIndex, and pIndex:

If the character m[mIndex] matches the character p[pIndex], we will take the matching result up to mIndex-1 and nIndex.
If the character n[nIndex] matches the character p[pIndex], we will take the matching result up to mIndex and nIndex-1.

String p will be interleaving strings m and n if any of the above two options is true. This is also required as there could be some common letters between m and n.

So our recursive formula would look like:

dp[mIndex][nIndex] = false

if m[mIndex] == p[pIndex]

` dp[mIndex][nIndex] = dp[mIndex-1][nIndex]`

if n[nIndex] == p[pIndex]

` dp[mIndex][nIndex] |= dp[mIndex][nIndex-1]`

Brainscape's Knowledge GenomeTM

Dynamic Programming Strategies Flashcards

Brainscape's Knowledge Genome^TM