Array Strategies Flashcards
(12 cards)
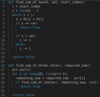
Binary Search

Given a sorted array of integers, return the index of the given key. Return -1 if not found.
Logarithmic, O(logn) Runtime, Logarithmic, O(logn) Memory
Binary search is used to find the index of an element in a sorted array. If the element doesn’t exist, that can be determined efficiently as well. The algorithm divides the input array by half at every step. After every step, either we have found the index that we are looking for or half of the array can be discarded. Hence, solution can be calculated in O(logn) time.
Here’s how the algorithm works.
At every step, consider the array between low and high indices
Calculate the mid index.
If the element at the mid index is the key, return mid.
If the element at mid is greater than the key, then reduce the array size such that high becomes mid - 1.
Index at low remains the same.
If the element at mid is less than the key, then reduce the array size such that low becomes mid + 1. Index at high remains the same.
When low is greater than high, key doesn’t exist. Return -1.
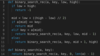
Find Maximum in Sliding Window

Given a large array of integers and a window of size w, find the current maximum value in the window as the window slides through the entire array.
O(n) runtime, O(w) memory, where ‘w’ is the window size.
The algorithm uses the deque data structure to find the maximum in a window. A deque is a double-ended queue in which push and pop operations work in O(1) at both ends. It will act as our window.
At the start of the algorithm, we search for the maximum value in the first window. The first element’s index is pushed to the front of the deque.
If an element is smaller than the one at the back of the queue, it is pushed in and becomes the new back. If the current element is larger, the back of the queue is popped repeatedly until we can find a value which is higher and then we’ll push the current element in as the new back.
As we can see, the deque stores elements in decreasing order. The front of the deque contains the index for the maximum value in that particular window.
We will repeat the following steps each time our window moves to the right:
- Remove all elements’ indices from the back of the deque which are smaller than, or equal to the current element
- remove the element index at the front if its value no longer falls in the current window
- push the current element index at the back of window
- current max is at the front
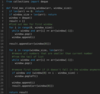
Search Rotated Array

Search for a given number in a sorted array that has been rotated by some arbitrary number. Return -1 if the number does not exist. Assume that the array does not contain duplicates.
Logarithmic, O(logn) runtime, Logarithmic, O(logn) memory
The solution is essentially binary search but with some modifications. If we look at the array in the example closely, we notice that at least one half of the array is always sorted. We can use this property to our advantage. If the number n lies within the sorted half of the array, then our problem is a basic binary search. Otherwise discard the sorted half and keep examining the unsorted half. Since we are partitioning the array in half at each step this gives us O(logn) runtime complexity.
The pythonic solution works iteratively, and so, the memory complexity of this algorithm comes down to O(1).
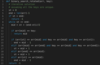
Find the Smallest Common Number
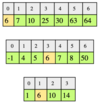
In the example below, you are given three integer arrays sorted in ascending order, and you have to find the smallest number that is common in all three arrays.
Linear, O(n) Runtime, Constant Memory
We should try to think of a way where we can take advantage of the fact that the arrays are sorted in ascending order. We will use three iterators simultaneously to traverse each of the arrays. We can start by traversing the arrays starting from the 0th index, which will have the smallest value of each array. If the values at the array indices pointed to by the three iterators are equal, that’s the solution since that will be the smallest value (as arrays are sorted in ascending order) present in all of the arrays. Then, we’ll just return the value. Otherwise, we’ll see which iterator amongst the three points to the smallest value and will increment that iterator so that it will point to the next index. If any of the three iterators reaches the end of the array while we haven’t found the common number, we’ll return -1.
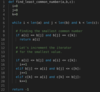
Rotate Array
Given an array of integers, rotate the array by N elements where N is an integer.
Linear, O(n) runtime, Constant complexity O(n)
The Pythonic way is super easy, it’s just the following:
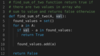
def rotate_array(arr, n):
` return arr[-n:] + arr[:-n]`
Find Low/High index

Given a sorted array of integers, return the low and high index of the given key. Return -1 if not found. The array length can be in the millions with many duplicates.
In the following example, low and high indices would be:
Key: 1, Low=0 and High=0
Key: 2, Low=1 and High=1
Key: 5, Low=2 and High=9
key: 20, Low=10 and High=10
Binary search twice, so O(logn) runtime, O(1) Complexity.
Linearly scanning the sorted array for low and high indices is highly inefficient since our array size is in millions. Instead, we will use slightly modified binary search to find the low and high indices of a given key. We need to do binary search twice; once for finding the low index and once for finding the high index.
Let’s look at the algorithm for finding the low index.
- At every step, consider the array between low and high indices
- Calculate the mid index.
- If element at mid index is less than the key, low becomes mid + 1 (to move towards start of range)
- If element at mid is greater or equal to the key, high becomes mid - 1. Index at low remains the same.
- When low is greater than high, low would be pointing to the first occurrence of the key.
- If element at low does not match the key, return -1.
Similarly, we can find the high index by slightly modifying the above condition to switch low index to mid+1 when element at mid index is less than or equal to the key and to switch the high index to mid-1 when element at mid is greater than the key.
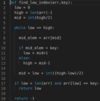
Move zeros to left

Given an integer array, move all elements that are equal to 0 to the left while maintaining the order of other elements in the array.
Linear Runtime, Constant Memory
We will keep two markers (read_index and write_index) and point them to the end of the array. Here is an overview of the algorithm.
While moving read_index towards the start of the array:
if read_index points to ‘0’, skip
if read_index points to non-zero, write to write_index and decrement write_index
Find maximum single sell profit

Given a list of daily stock prices (integers for simplicity), return the buy and sell prices for making the maximum profit. We need to maximize the single buy/sell profit. If we can’t make any profit, we’ll try to minimize the loss.
Linear Runtime, Constant Memory
There is a tricky linear solution to this problem that requires maintaining current buy price (which is the smallest number seen so far), current profit, and global max profit as we iterate through the entire array of stock prices. At each iteration, we will compare the current profit with the global profit and update the global profit accordingly.
Basic algorithm is as follows:
current profit = INT_MIN
current buy = stock_prices[0]
global sell = stock_prices[1]
global profit = global sell - current buy
For i = 1 to stock_prices.length:
current profit = stock_prices[i] - current buy
if current profit is greater than global profit
then update global profit to current profit and update global sell to stock_prices[i]
if stock_prices[i] is less than current buy then update current buy to stock_prices[i]
return global profit and global sell
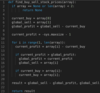
Implement Quicksort

Given an integer array, sort it in ascending order using quicksort.
Linearithmic O(nlogn) Runtime, Logarithmic O(logn) Memory
Here is an overview of how the quicksort algorithm works.
Select a pivot element from the array. We can pick the first element as the pivot if we follow Hoare’s algorithm. Another common approach is to select a random element as the pivot.
Reorder the array by comparing with the pivot element such that smaller values end up at the left side, and larger values end up at the right side of the pivot.
Now, the pivot element is in its correct sorted position.
Applying the above steps, we can recursively sort the sublists on the right and left sides of the pivot.
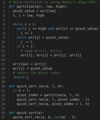
Merge Overlapping Intervals
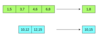
You are given an array (list) of interval pairs as input where each interval has a start and end timestamp. The input array is sorted by starting timestamps. You are required to merge overlapping intervals and return output array (list).
Linear Runtime, Linear Memory
This problem can be solved in a simple linear scan algorithm. We know that input is sorted by starting timestamps. Here is the approach we are following. List of input intervals is given, and we’ll keep merged intervals in the output list For each interval in the input list if the input interval is overlapping with the last interval in output list then we’ll merge these two intervals and update the last interval of output list with merged interval otherwise, we’ll add an input interval to the output list.
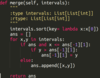
Sum of Two Values

Given an array of integers and a value, determine if there are any two integers in the array whose sum is equal to the given value.
Linear Runtime, Linear Memory
In this solution, we’ll use the following algorithm to find a pair that add up to the target (say ‘val’). Scan the whole array once and store visited elements in a hash set. During scan, for every element ‘e’ in the array, we check if ‘val’ - ‘e’ is present in the hash set i.e. ‘val’ - ‘e’ is already visited. If ‘val’ - ‘e’ is found in the hash set, it means there is a pair (e, val - e) in array whose sum is equal to the given val. If we have exhausted all elements in the array and didn’t find any such pair, the function will return false.
Sum of Three Values

Given an array of integers and a value, determine if there are any three integers in the array whose sum equals the given value.
Consider this array and the target sums.
Quadratic, O(n2) Memory, Constant O(1) Runtiime
To understand this solution better, we recommend taking a look at “Sum of Two Values”.
In this solution, we first sort the array. Then we fix one element ‘e’, and try to find a pair (a, b) in the remaining array such that required_sum - e = a + b.
We start with the first element e in the array (at index i = 0) and try to find such a pair (a, b) in the remaining array (i.e A[i + 1] to A[n - 1]) that satisfies the condition: a+b = required_sum - e. We can find such a pair in linear time. If we find such a pair, we have found the solution: a, b and e and thus, we can stop the iteration.
Otherwise, we repeat the above steps for all elements e at index i = 1 to n - 3, until we find a pair that meets the condition.