InPlace Reversal of LinkedList Flashcards
(5 cards)
Reverse a LinkedList
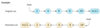
Given the head of a Singly LinkedList, reverse the LinkedList. Write a function to return the new head of the reversed LinkedList.
To reverse a LinkedList, we need to reverse one node at a time. We will start with a variable current which will initially point to the head of the LinkedList and a variable previous which will point to the previous node that we have processed; initially previous will point to null.
In a stepwise manner, we will reverse the current node by pointing it to the previous before moving on to the next node. Also, we will update the previous to always point to the previous node that we have processed.
The time complexity of our algorithm will be O(N) where ‘N’ is the total number of nodes in the LinkedList.
We only used constant space, therefore, the space complexity of our algorithm is O(1).
Reverse a Sub-list
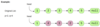
Given the head of a LinkedList and two positions ‘p’ and ‘q’, reverse the LinkedList from position ‘p’ to ‘q’.
The problem follows the In-place Reversal of a LinkedList pattern. We can use a similar approach as discussed in Reverse a LinkedList. Here are the steps we need to follow:
- Skip the first p-1 nodes, to reach the node at position p.
- Remember the node at position p-1 to be used later to connect with the reversed sub-list.
- Next, reverse the nodes from p to q using the same approach discussed in Reverse a LinkedList.
- Connect the p-1 and q+1 nodes to the reversed sub-list.
The time complexity of our algorithm will be O(N) where ‘N’ is the total number of nodes in the LinkedList.
We only used constant space, therefore, the space complexity of our algorithm is O(1).
Reverse every K-element Sub-list

Given the head of a LinkedList and a number ‘k’, reverse every ‘k’ sized sub-list starting from the head.
If, in the end, you are left with a sub-list with less than ‘k’ elements, reverse it too.
The problem follows the In-place Reversal of a LinkedList pattern and is quite similar to Reverse a Sub-list. The only difference is that we have to reverse all the sub-lists. We can use the same approach, starting with the first sub-list (i.e. p=1, q=k) and keep reversing all the sublists of size ‘k’.
The time complexity of our algorithm will be O(N) where ‘N’ is the total number of nodes in the LinkedList.
We only used constant space, therefore, the space complexity of our algorithm is O(1).
Reverse alternating K-element Sub-list

Given the head of a LinkedList and a number ‘k’, reverse every alternating ‘k’ sized sub-list starting from the head.
If, in the end, you are left with a sub-list with less than ‘k’ elements, reverse it too.
The problem follows the In-place Reversal of a LinkedList pattern and is quite similar to Reverse every K-element Sub-list. The only difference is that we have to skip ‘k’ alternating elements. We can follow a similar approach, and in each iteration after reversing ‘k’ elements, we will skip the next ‘k’ elements.
The time complexity of our algorithm will be O(N) where ‘N’ is the total number of nodes in the LinkedList.
We only used constant space, therefore, the space complexity of our algorithm is O(1).

Rotate a LinkedList
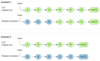
Given the head of a Singly LinkedList and a number ‘k’, rotate the LinkedList to the right by ‘k’ nodes.
Another way of defining the rotation is to take the sub-list of ‘k’ ending nodes of the LinkedList and connect them to the beginning. Other than that we have to do three more things:
- Connect the last node of the LinkedList to the head, because the list will have a different tail after the rotation.
- The new head of the LinkedList will be the node at the beginning of the sublist.
- The node right before the start of sub-list will be the new tail of the rotated LinkedList.
The time complexity of our algorithm will be O(N) where ‘N’ is the total number of nodes in the LinkedList.
We only used constant space, therefore, the space complexity of our algorithm is O(1).



