Merge Intervals Problems Flashcards
Merge Intervals
Given a list of intervals, merge all the overlapping intervals to produce a list that has only mutually exclusive intervals.
Example 1
Intervals: [[1,4], [2,5], [7,9]]
Output: [[1,5], [7,9]]
Explanation: Since the first two intervals [1,4] and [2,5] overlap, we merged them into one [1,5].
Example 2
Intervals: [[6,7], [2,4], [5,9]]
Output: [[2,4], [5,9]]
Explanation: Since the intervals [6,7] and [5,9] overlap, we merged them into one [5,9].
Example 3
Intervals: [[1,4], [2,6], [3,5]]
Output: [[1,6]]
Explanation: Since all the given intervals overlap, we merged them into one.
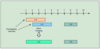
Let’s take the example of two intervals (‘a’ and ‘b’) such that a.start <= b.start. There are three possible scenarios:
Our goal is to merge the intervals whenever they overlap. For the above-mentioned two overlapping scenarios (2 and 3), this is how we will merge them:
The diagram above clearly shows a merging approach. Our algorithm will look like this:
Sort the intervals on the start time to ensure a.start <= b.start
If ‘a’ overlaps ‘b’ (i.e. b.start <= a.end), we need to merge them into a new interval ‘c’ such that:
c.start = a.start c.end = max(a.end, b.end)
Insert Interval
Given a list of non-overlapping intervals sorted by their start time, insert a given interval at the correct position and merge all necessary intervals to produce a list that has only mutually exclusive intervals.
Example 1
Input: Intervals=[[1,3], [5,7], [8,12]], New Interval=[4,6]
Output: [[1,3], [4,7], [8,12]]
Explanation: After insertion, since [4,6] overlaps with [5,7], we merged them into one [4,7].
Example 2
Input: Intervals=[[1,3], [5,7], [8,12]], New Interval=[4,10]
Output: [[1,3], [4,12]]
Explanation: After insertion, since [4,10] overlaps with [5,7] & [8,12], we merged them into [4,12].
Example 3
Input: Intervals=[[2,3],[5,7]], New Interval=[1,4]
Output: [[1,4], [5,7]]
Explanation: After insertion, since [1,4] overlaps with [2,3], we merged them into one [1,4].
If the given list was not sorted, we could have simply appended the new interval to it and used the merge() function from Merge Intervals. But since the given list is sorted, we should try to come up with a solution better than O(N * logN)
When inserting a new interval in a sorted list, we need to first find the correct index where the new interval can be placed. In other words, we need to skip all the intervals which end before the start of the new interval. So we can iterate through the given sorted listed of intervals and skip all the intervals with the following condition:
intervals[i].end
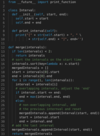
Once we have found the correct place, we can follow an approach similar to Merge Intervals to insert and/or merge the new interval. Let’s call the new interval ‘a’ and the first interval with the above condition ‘b’. There are five possibilities:
The diagram above clearly shows the merging approach. To handle all four merging scenarios, we need to do something like this:
c.start = min(a.start, b.start) c.end = max(a.end, b.end)
Our overall algorithm will look like this:
Skip all intervals which end before the start of the new interval, i.e., skip all intervals with the following condition:
intervals[i].end
Let’s call the last interval ‘b’ that does not satisfy the above condition. If ‘b’ overlaps with the new interval (a) (i.e. b.start <= a.end), we need to merge them into a new interval ‘c’:
c.start = min(a.start, b.start) c.end = max(a.end, b.end)
We will repeat the above two steps to merge ‘c’ with the next overlapping interval.
Intervals Intersection
Given two lists of intervals, find the intersection of these two lists. Each list consists of disjoint intervals sorted on their start time.
Example 1
Input: arr1=[[1, 3], [5, 6], [7, 9]], arr2=[[2, 3], [5, 7]]
Output: [2, 3], [5, 6], [7, 7]
Explanation: The output list contains the common intervals between the two lists.
Example 2
Input: arr1=[[1, 3], [5, 7], [9, 12]], arr2=[[5, 10]]
Output: [5, 7], [9, 10]
Explanation: The output list contains the common intervals between the two lists.
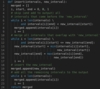
This problem follows the Merge Intervals pattern. As we have discussed under Insert Interval, there are five overlapping possibilities between two intervals ‘a’ and ‘b’:
So there are four scenarios when the two intervals overlap (2-5). Close observation will reveal that whenever the two intervals overlap, one of the interval’s start time lies within the other interval. This rule can help us identify if any two intervals overlap or not.
Secondly, if we have found that two intervals overlap, how can we find the overlapped part?
Again from the above diagram, the overlapping interval will be equal to:
start = max(a.start, b.start) end = min(a.end, b.end)
That is, the highest start time and the lowest end time will be the overlapping interval.
So our algorithm will be to iterate through both the lists together to see if any two intervals overlap. If two intervals overlap, we will insert the overlapped part into a result list and move on to the next interval which is finishing early.
As we are iterating through both the lists once, the time complexity of the above algorithm is O(N + M), where ‘N’ and ‘M’ are the total number of intervals in the input arrays respectively.
Ignoring the space needed for the result list, the algorithm runs in constant space O(1).
Conflicting Appointments
Given an array of intervals representing ‘N’ appointments, find out if a person can attend all the appointments.
Example 1
Appointments: [[1,4], [2,5], [7,9]]
Output: false
Explanation: Since [1,4] and [2,5] overlap, a person cannot attend both of these appointments.
Example 2
Appointments: [[6,7], [2,4], [8,12]]
Output: true
Explanation: None of the appointments overlap, therefore a person can attend all of them.
Example 3
Appointments: [[4,5], [2,3], [3,6]]
Output: false
Explanation: Since [4,5] and [3,6] overlap, a person cannot attend both of these appointments.
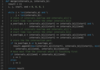
The problem follows the Merge Intervals pattern. We can sort all the intervals by start time and then check if any two intervals overlap. A person will not be able to attend all appointments if any two appointments overlap.
The time complexity of the above algorithm is O(N*logN), where ‘N’ is the total number of appointments. Though we are iterating the intervals only once, our algorithm will take O(N * logN) since we need to sort them in the beginning.
The space complexity of the above algorithm will be O(N), which we need for sorting. For Java, Arrays.sort() uses Timsort, which needs O(N) space.
Minimum Meeting Rooms

Given a list of intervals representing the start and end time of ‘N’ meetings, find the minimum number of rooms required to hold all the meetings.
Example 1
Meetings: [[1,4], [2,5], [7,9]]
Output: 2
Explanation: Since [1,4] and [2,5] overlap, we need two rooms to hold these two meetings. [7,9] can occur in any of the two rooms later.
Example 2
Meetings: [[6,7], [2,4], [8,12]]
Output: 1
Explanation: None of the meetings overlap, therefore we only need one room to hold all meetings.
Example 3
Meetings: [[1,4], [2,3], [3,6]]
Output:2
Explanation: Since [1,4] overlaps with the other two meetings [2,3] and [3,6], we need two rooms to hold all the meetings.
Example 4
Meetings: [[4,5], [2,3], [2,4], [3,5]]
Output: 2
Explanation: We will need one room for [2,3] and [3,5], and another room for [2,4] and [4,5].
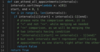
we need to keep track of the ending time of all the meetings currently happening so that when we try to schedule a new meeting, we can see what meetings have already ended. We need to put this information in a data structure that can easily give us the smallest ending time. A Min Heap would fit our requirements best.
So our algorithm will look like this:
- Sort all the meetings on their start time.
- Create a min-heap to store all the active meetings. This min-heap will also be used to find the active meeting with the smallest end time.
- Iterate through all the meetings one by one to add them in the min-heap. Let’s say we are trying to schedule the meeting m1.
- Since the min-heap contains all the active meetings, so before scheduling m1 we can remove all meetings from the heap that have ended before m1, i.e., remove all meetings from the heap that have an end time smaller than or equal to the start time of m1.
- Now add m1 to the heap.
- The heap will always have all the overlapping meetings, so we will need rooms for all of them. Keep a counter to remember the maximum size of the heap at any time which will be the minimum number of rooms needed.
The time complexity of the above algorithm is O(N*logN), where ‘N’ is the total number of meetings. This is due to the sorting that we did in the beginning. Also, while iterating the meetings we might need to poll/offer meeting to the priority queue. Each of these operations can take O(logN). Overall our algorithm will take O(NlogN).
The space complexity of the above algorithm will be O(N) which is required for sorting. Also, in the worst case scenario, we’ll have to insert all the meetings into the Min Heap (when all meetings overlap) which will also take O(N) space. The overall space complexity of our algorithm is O(N).
Maximum CPU Load
We are given a list of Jobs. Each job has a Start time, an End time, and a CPU load when it is running. Our goal is to find the maximum CPU load at any time if all the jobs are running on the same machine.
Example 1
Jobs: [[1,4,3], [2,5,4], [7,9,6]]
Output: 7
Explanation: Since [1,4,3] and [2,5,4] overlap, their maximum CPU load (3+4=7) will be when both the jobs are running at the same time i.e., during the time interval (2,4).
Example 2
Jobs: [[6,7,10], [2,4,11], [8,12,15]]
Output: 15
Explanation: None of the jobs overlap, therefore we will take the maximum load of any job which is 15.
Example 3
Jobs: [[1,4,2], [2,4,1], [3,6,5]]
Output: 8
Explanation: Maximum CPU load will be 8 as all jobs overlap during the time interval [3,4].
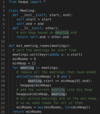
The problem follows the Merge Intervals pattern and can easily be converted to Minimum Meeting Rooms. Similar to ‘Minimum Meeting Rooms’ where we were trying to find the maximum number of meetings happening at any time, for ‘Maximum CPU Load’ we need to find the maximum number of jobs running at any time. We will need to keep a running count of the maximum CPU load at any time to find the overall maximum load.
The time complexity of the above algorithm is O(N*logN), where ‘N’ is the total number of jobs. This is due to the sorting that we did in the beginning. Also, while iterating the jobs, we might need to poll/offer jobs to the priority queue. Each of these operations can take O(logN). Overall our algorithm will take O(NlogN).
The space complexity of the above algorithm will be O(N), which is required for sorting. Also, in the worst case, we have to insert all the jobs into the priority queue (when all jobs overlap) which will also take O(N) space. The overall space complexity of our algorithm is O(N).
Employee Free Time
For ‘K’ employees, we are given a list of intervals representing the working hours of each employee. Our goal is to find out if there is a free interval that is common to all employees. You can assume that each list of employee working hours is sorted on the start time.
Example 1
Input: Employee Working Hours=[[[1,3], [5,6]], [[2,3], [6,8]]]
Output: [3,5]
Explanation: Both the employess are free between [3,5].
Example 2
Input: Employee Working Hours=[[[1,3], [9,12]], [[2,4]], [[6,8]]]
Output: [4,6], [8,9]
Explanation: All employess are free between [4,6] and [8,9].
Example 3
Input: Employee Working Hours=[[[1,3]], [[2,4]], [[3,5], [7,9]]]
Output: [5,7]
Explanation: All employess are free between [5,7].
One simple solution can be to put the working hours of all employees in a list and sort them on the start time. Then we can iterate through the list to find the gaps. Let’s dig deeper. Sorting the intervals of the above example will give us:
[1,3], [2,4], [6,8], [9,12]
We can now iterate through these intervals, and whenever we find non-overlapping intervals (e.g., [2,4] and [6,8]), we can calculate a free interval (e.g., [4,6]). This algorithm will take O(N * logN) time, where ‘N’ is the total number of intervals. This time is needed because we need to sort all the intervals. The space complexity will be O(N), which is needed for sorting. Can we find a better solution?
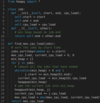
Using a Heap to Sort the Intervals
One fact that we are not utilizing is that each employee list is individually sorted!
How about we take the first interval of each employee and insert it in a Min Heap. This Min Heap can always give us the interval with the smallest start time. Once we have the smallest start-time interval, we can then compare it with the next smallest start-time interval (again from the Heap) to find the gap. This interval comparison is similar to what we suggested in the previous approach.
Whenever we take an interval out of the Min Heap, we can insert the next interval of the same employee. This also means that we need to know which interval belongs to which employee.
The time complexity of the above algorithm is O(N*logK), where ‘N’ is the total number of intervals and ‘K’ is the total number of employees. This is due to the fact that we are iterating through the intervals only once (which will take O(N)), and every time we process an interval, we remove (and can insert) one interval in the Min Heap, (which will take O(logK). At any time the heap will not have more than ‘K’ elements.
The space complexity of the above algorithm will be O(K) as at any time the heap will not have more than ‘K’ elements.