Topological Sort (Graph) Strategies

Question 1

Answer 1

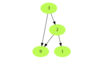
The basic idea behind the topological sort is to provide a partial ordering among the vertices of the graph such that if there is an edge from U to V then U≤V i.e., U comes before V in the ordering. Here are a few fundamental concepts related to topological sort:

1. Source: Any node that has no incoming edge and has only outgoing edges is called a source.
2. Sink: Any node that has only incoming edges and no outgoing edge is called a sink.
3. So, we can say that a topological ordering starts with one of the sources and ends at one of the sinks.
4. A topological ordering is possible only when the graph has no directed cycles, i.e. if the graph is a Directed Acyclic Graph (DAG). If the graph has a cycle, some vertices will have cyclic dependencies which makes it impossible to find a linear ordering among vertices.

To find the topological sort of a graph we can traverse the graph in a Breadth First Search (BFS) way. We will start with all the sources, and in a stepwise fashion, save all sources to a sorted list. We will then remove all sources and their edges from the graph. After the removal of the edges, we will have new sources, so we will repeat the above process until all vertices are visited.

This is how we can implement this algorithm:

a. Initialization

We will store the graph in Adjacency Lists, which means each parent vertex will have a list containing all of its children. We will do this using a HashMap where the ‘key’ will be the parent vertex number and the value will be a List containing children vertices.

To find the sources, we will keep a HashMap to count the in-degrees i.e., count of incoming edges of each vertex. Any vertex with ‘0’ in-degree will be a source.

b. Build the graph and find in-degrees of all vertices

We will build the graph from the input and populate the in-degrees HashMap.

c. Find all sources

All vertices with ‘0’ in-degrees will be our sources and we will store them in a Queue.

d. Sort

For each source, do the following things:

Add it to the sorted list.

Get all of its children from the graph.

Decrement the in-degree of each child by 1.

If a child’s in-degree becomes ‘0’, add it to the sources Queue.

Repeat step 1, until the source Queue is empty.

In step ‘d’, each vertex will become a source only once and each edge will be accessed and removed once. Therefore, the time complexity of the above algorithm will be O(V+E), where ‘V’ is the total number of vertices and ‘E’ is the total number of edges in the graph.

The space complexity will be O(V+E), since we are storing all of the edges for each vertex in an adjacency list.

Answer 2

This problem is asking us to find out if it is possible to find a topological ordering of the given tasks. The tasks are equivalent to the vertices and the prerequisites are the edges.

We can use a similar algorithm as described in Topological Sort to find the topological ordering of the tasks. If the ordering does not include all the tasks, we will conclude that some tasks have cyclic dependencies.

In step ‘d’, each task can become a source only once and each edge (prerequisite) will be accessed and removed once. Therefore, the time complexity of the above algorithm will be O(V+E), where ‘V’ is the total number of tasks and ‘E’ is the total number of prerequisites.

The space complexity will be O(V+E), since we are storing all of the prerequisites for each task in an adjacency list.

Question 3

Tasks Scheduling Order

There are ‘N’ tasks, labeled from ‘0’ to ‘N-1’. Each task can have some prerequisite tasks which need to be completed before it can be scheduled. Given the number of tasks and a list of prerequisite pairs, write a method to find the ordering of tasks we should pick to finish all tasks.

Example 1
Input: Tasks=3, Prerequisites=[0, 1], [1, 2]
Output: [0, 1, 2]
Explanation: To execute task ‘1’, task ‘0’ needs to finish first. Similarly, task ‘1’ needs to finish before ‘2’ can be scheduled. A possible scheduling of tasks is: [0, 1, 2]

Example 2
Input: Tasks=3, Prerequisites=[0, 1], [1, 2], [2, 0]
Output: []
Explanation: The tasks have cyclic dependency, therefore they cannot be scheduled.

Example 3
Input: Tasks=6, Prerequisites=[2, 5], [0, 5], [0, 4], [1, 4], [3, 2], [1, 3]
Output: [0 1 4 3 2 5]
Explanation: A possible scheduling of tasks is: [0 1 4 3 2 5]

Answer 3

This problem is similar to Tasks Scheduling, the only difference being that we need to find the best ordering of tasks so that it is possible to schedule them all.

In step ‘d’, each task can become a source only once and each edge (prerequisite) will be accessed and removed once. Therefore, the time complexity of the above algorithm will be O(V+E), where ‘V’ is the total number of tasks and ‘E’ is the total number of prerequisites.

The space complexity will be O(V+E), since we are storing all of the prerequisites for each task in an adjacency list.

Question 4

All Tasks Scheduling Orders

There are ‘N’ tasks, labeled from ‘0’ to ‘N-1’. Each task can have some prerequisite tasks which need to be completed before it can be scheduled. Given the number of tasks and a list of prerequisite pairs, write a method to print all possible ordering of tasks meeting all prerequisites.

Example 1
Input: Tasks=3, Prerequisites=[0, 1], [1, 2]
Output: [0, 1, 2]
Explanation: There is only possible ordering of the tasks.

Example 2
Input: Tasks=4, Prerequisites=[3, 2], [3, 0], [2, 0], [2, 1]
Output:
1) [3, 2, 0, 1]
2) [3, 2, 1, 0]
Explanation: There are two possible orderings of the tasks meeting all prerequisites.

Example 3
Input: Tasks=6, Prerequisites=[2, 5], [0, 5], [0, 4], [1, 4], [3, 2], [1, 3]
Output:
1) [0, 1, 4, 3, 2, 5]
2) [0, 1, 3, 4, 2, 5]
3) [0, 1, 3, 2, 4, 5]
4) [0, 1, 3, 2, 5, 4]
5) [1, 0, 3, 4, 2, 5]
6) [1, 0, 3, 2, 4, 5]
7) [1, 0, 3, 2, 5, 4]
8) [1, 0, 4, 3, 2, 5]
9) [1, 3, 0, 2, 4, 5]
10) [1, 3, 0, 2, 5, 4]
11) [1, 3, 0, 4, 2, 5]
12) [1, 3, 2, 0, 5, 4]
13) [1, 3, 2, 0, 4, 5]

Answer 4

This problem is similar to Tasks Scheduling Order, the only difference is that we need to find all the topological orderings of the tasks.

At any stage, if we have more than one source available and since we can choose any source, therefore, in this case, we will have multiple orderings of the tasks. We can use a recursive approach with Backtracking to consider all sources at any step.

If we don’t have any prerequisites, all combinations of the tasks can represent a topological ordering. As we know, that there can be N! combinations for ‘N’ numbers, therefore the time and space complexity of our algorithm will be O(V! * E) where ‘V’ is the total number of tasks and ‘E’ is the total prerequisites. We need the ‘E’ part because in each recursive call, at max, we remove (and add back) all the edges.

Question 5

Alien Dictionary

There is a dictionary containing words from an alien language for which we don’t know the ordering of the characters. Write a method to find the correct order of characters in the alien language.

Example 1
Input: Words: [“ba”, “bc”, “ac”, “cab”]
Output: bac
Explanation: Given that the words are sorted lexicographically by the rules of the alien language, so from the given words we can conclude the following ordering among its characters:
1. From “ba” and “bc”, we can conclude that ‘a’ comes before ‘c’.
2. From “bc” and “ac”, we can conclude that ‘b’ comes before ‘a’
From the above two points we can conclude that the correct character order is: “bac”

Example 2
Input: Words: [“cab”, “aaa”, “aab”]
Output: cab
Explanation: From the given words we can conclude the following ordering among its characters:
1. From “cab” and “aaa”, we can conclude that ‘c’ comes before ‘a’.
2. From “aaa” and “aab”, we can conclude that ‘a’ comes before ‘b’
From the above two points, we can conclude that the correct character order is: “cab”

Example 3
Input: Words: [“ywx”, “xww”, “xz”, “zyy”, “zwz”]
Output: yxwz
Explanation: From the given words we can conclude the following ordering among its characters:
1. From “ywx” and “xww”, we can conclude that ‘y’ comes before ‘x’.
2. From “xww” and “xz”, we can conclude that ‘w’ comes before ‘z’
3. From “xz” and “zyy”, we can conclude that ‘x’ comes before ‘z’
4. From “zyy” and “zwz”, we can conclude that ‘y’ comes before ‘w’
From the above two points we can conclude that the correct character order is: “yxwz”

Answer 5

Since the given words are sorted lexicographically by the rules of the alien language, we can always compare two adjacent words to determine the ordering of the characters.

This makes the current problem similar to Tasks Scheduling Order, the only difference being that we need to build the graph of the characters by comparing adjacent words first, and then perform the topological sort for the graph to determine the order of the characters.

In step ‘d’, each task can become a source only once and each edge (a rule) will be accessed and removed once. Therefore, the time complexity of the above algorithm will be O(V+E), where ‘V’ is the total number of different characters and ‘E’ is the total number of the rules in the alien language. Since, at most, each pair of words can give us one rule, therefore, we can conclude that the upper bound for the rules is O(N) where ‘N’ is the number of words in the input. So, we can say that the time complexity of our algorithm is O(V+N).

The space complexity will be O(V+N), since we are storing all of the rules for each character in an adjacency list.

Question 6

Reconstructing a Sequence

Given a sequence originalSeq and an array of sequences, write a method to find if originalSeq can be uniquely reconstructed from the array of sequences.

Unique reconstruction means that we need to find if originalSeq is the only sequence such that all sequences in the array are subsequences of it.

Example 1
Input: originalSeq: [1, 2, 3, 4], seqs: [[1, 2], [2, 3], [3, 4]]
Output: true
Explanation: The sequences [1, 2], [2, 3], and [3, 4] can uniquely reconstruct [1, 2, 3, 4], in other words, all the given sequences uniquely define the order of numbers in the ‘originalSeq’.

Example 2
Input: originalSeq: [1, 2, 3, 4], seqs: [[1, 2], [2, 3], [2, 4]]
Output: false
Explanation: The sequences [1, 2], [2, 3], and [2, 4] cannot uniquely reconstruct [1, 2, 3, 4]. There are two possible sequences we can construct from the given sequences: 1) [1, 2, 3, 4] 2) [1, 2, 4, 3]

Example 3
Input: originalSeq: [3, 1, 4, 2, 5], seqs: [[3, 1, 5], [1, 4, 2, 5]]
Output: true
Explanation: The sequences [3, 1, 5] and [1, 4, 2, 5] can uniquely reconstruct [3, 1, 4, 2, 5]. Given a sequence originalSeq and an array of sequences, write a method to find if originalSeq can be uniquely reconstructed from the array of sequences.

Answer 6

Since each sequence in the given array defines the ordering of some numbers, we need to combine all these ordering rules to find two things:

1. Is it possible to construct the originalSeq from all these rules?
2. Are these ordering rules not sufficient enough to define the unique ordering of all the numbers in the originalSeq? In other words, can these rules result in more than one sequence?

This makes the current problem similar to Tasks Scheduling Order with two differences:

1. We need to build the graph of the numbers by comparing each pair of numbers in the given array of sequences.
2. We must perform the topological sort for the graph to determine two things:

• Can the topological ordering construct the originalSeq?
• That there is only one topological ordering of the numbers possible. This can be confirmed if we do not have more than one source at any time while finding the topological ordering of numbers.

In step ‘d’, each number can become a source only once and each edge (a rule) will be accessed and removed once. Therefore, the time complexity of the above algorithm will be O(V+E), where ‘V’ is the count of distinct numbers and ‘E’ is the total number of the rules. Since, at most, each pair of numbers can give us one rule, we can conclude that the upper bound for the rules is O(N) where ‘N’ is the count of numbers in all sequences. So, we can say that the time complexity of our algorithm is O(V+N).

The space complexity will be O(V+N), since we are storing all of the rules for each number in an adjacency list.

Question 7

Minimum Height Trees

We are given an undirected graph that has characteristics of a k-ary tree. In such a graph, we can choose any node as the root to make a k-ary tree. The root (or the tree) with the minimum height will be called Minimum Height Tree (MHT). There can be multiple MHTs for a graph. In this problem, we need to find all those roots which give us MHTs. Write a method to find all MHTs of the given graph and return a list of their roots.

Example 1
Input: vertices: 5, Edges: [[0, 1], [1, 2], [1, 3], [2, 4]]
Output: [1, 2]
Explanation: Choosing ‘1’ or ‘2’ as roots give us MHTs. In the below diagram, we can see that the height of the trees with roots ‘1’ or ‘2’ is three which is minimum.

Answer 7

From the above-mentioned examples, we can clearly see that any leaf node (i.e., node with only one edge) can never give us an MHT because its adjacent non-leaf nodes will always give an MHT with a smaller height. All the adjacent non-leaf nodes will consider the leaf node as a subtree. Let’s understand this with another example. Suppose we have a tree with root ‘M’ and height ‘5’. Now, if we take another node, say ‘P’, and make the ‘M’ tree as its subtree, then the height of the overall tree with root ‘P’ will be ‘6’ (=5+1). Now, this whole tree can be considered a graph, where ‘P’ is a leaf as it has only one edge (connection with ‘M’). This clearly shows that the leaf node (‘P’) gives us a tree of height ‘6’ whereas its adjacent non-leaf node (‘M’) gives us a tree with smaller height ‘5’ - since ‘P’ will be a child of ‘M’.

This gives us a strategy to find MHTs. Since leaves can’t give us MHT, we can remove them from the graph and remove their edges too. Once we remove the leaves, we will have new leaves. Since these new leaves can’t give us MHT, we will repeat the process and remove them from the graph too. We will prune the leaves until we are left with one or two nodes which will be our answer and the roots for MHTs.

We can implement the above process using the topological sort. Any node with only one edge (i.e., a leaf) can be our source and, in a stepwise fashion, we can remove all sources from the graph to find new sources. We will repeat this process until we are left with one or two nodes in the graph, which will be our answer.

In step ‘d’, each node can become a source only once and each edge will be accessed and removed once. Therefore, the time complexity of the above algorithm will be O(V+E), where ‘V’ is the total nodes and ‘E’ is the total number of the edges.

The space complexity will be O(V+E), since we are storing all of the edges for each node in an adjacency list.