Subset Problems Flashcards
(9 cards)
Subsets
Given a set with distinct elements, find all of its distinct subsets.
Example 1
Input: [1, 3]
Output: [], [1], [3], [1,3]
Example 2
Input: [1, 5, 3]
Output: [], [1], [5], [3], [1,5], [1,3], [5,3], [1,5,3]
To generate all subsets of the given set, we can use the Breadth First Search (BFS) approach. We can start with an empty set, iterate through all numbers one-by-one, and add them to existing sets to create new subsets.
Since, in each step, the number of subsets doubles as we add each element to all the existing subsets, the time complexity of the above algorithm is O(2N), where ‘N’ is the total number of elements in the input set. This also means that, in the end, we will have a total of O(2N) subsets.
All the additional space used by our algorithm is for the output list. Since we will have a total of O(2N) subsets, the space complexity of our algorithm is also O(2N).
Subsets With Duplicates
Given a set of numbers that might contain duplicates, find all of its distinct subsets.
Example 1
Input: [1, 3, 3]
Output: [], [1], [3], [1,3], [3,3], [1,3,3]
Example 2
Input: [1, 5, 3, 3]
Output: [], [1], [5], [3], [1,5], [1,3], [5,3], [1,5,3], [3,3], [1,3,3], [3,3,5], [1,5,3,3]
This problem follows the Subsets pattern and we can follow a similar Breadth First Search (BFS) approach. The only additional thing we need to do is handle duplicates. Since the given set can have duplicate numbers, if we follow the same approach discussed in Subsets, we will end up with duplicate subsets, which is not acceptable. To handle this, we will do two extra things:
Sort all numbers of the given set. This will ensure that all duplicate numbers are next to each other.
Follow the same BFS approach but whenever we are about to process a duplicate (i.e., when the current and the previous numbers are same), instead of adding the current number (which is a duplicate) to all the existing subsets, only add it to the subsets which were created in the previous step.
Permutations
Given a set of distinct numbers, find all of its permutations.
Permutation is defined as the re-arranging of the elements of the set. For example, {1, 2, 3} has the following six permutations:
- {1, 2, 3}
- {1, 3, 2}
- {2, 1, 3}
- {2, 3, 1}
- {3, 1, 2}
- {3, 2, 1}
If a set has ‘n’ distinct elements it will have n! permutations.
Example 1
Input: [1,3,5]
Output: [1,3,5], [1,5,3], [3,1,5], [3,5,1], [5,1,3], [5,3,1]
This problem follows the Subsets pattern and we can follow a similar Breadth First Search (BFS) approach. However, unlike Subsets, every permutation must contain all the numbers.
We know that there are a total of N! permutations of a set with ‘N’ numbers. In the algorithm above, we are iterating through all of these permutations with the help of the two ‘for’ loops. In each iteration, we go through all the current permutations to insert a new number in them on line 17 (line 23 for C++ solution). To insert a number into a permutation of size ‘N’ will take O(N), which makes the overall time complexity of our algorithm O(N*N!).
All the additional space used by our algorithm is for the result list and the queue to store the intermediate permutations. If you see closely, at any time, we don’t have more than N! permutations between the result list and the queue. Therefore the overall space complexity to store N! permutations each containing N elements will be O(N*N!).

String Permutations by changing case
Given a string, find all of its permutations preserving the character sequence but changing case.
Example 1
Input: “ad52”
Output: “ad52”, “Ad52”, “aD52”, “AD52”
Example 2
Input: “ab7c”
Output: “ab7c”, “Ab7c”, “aB7c”, “AB7c”, “ab7C”, “Ab7C”, “aB7C”, “AB7C”
This problem follows the Subsets pattern and can be mapped to Permutations.
Following a BFS approach, we will consider one character at a time. Since we need to preserve the character sequence, we can start with the actual string and process each character (i.e., make it upper-case or lower-case) one by one.
Since we can have 2N permutations at the most and while processing each permutation we convert it into a character array, the overall time complexity of the algorithm will be O(N*2N).
All the additional space used by our algorithm is for the output list. Since we can have a total of O(2N) permutations, the space complexity of our algorithm is O(N*2N).
Balanced Parentheses
For a given number ‘N’, write a function to generate all combination of ‘N’ pairs of balanced parentheses.
Example 1
Input: N=2
Output: (()), ()()
Example 2
Input: N=3
Output: ((())), (()()), (())(), ()(()), ()()()
This problem follows the Subsets pattern and can be mapped to Permutations. We can follow a similar BFS approach.
Let’s take Example-2 mentioned above to generate all the combinations of balanced parentheses. Following a BFS approach, we will keep adding open parentheses ( or close parentheses ). At each step we need to keep two things in mind:
- We can’t add more than ‘N’ open parenthesis.
- To keep the parentheses balanced, we can add a close parenthesis ) only when we have already added enough open parenthesis (. For this, we can keep a count of open and close parenthesis with every combination.
Let’s try to estimate how many combinations we can have for ‘N’ pairs of balanced parentheses. If we don’t care for the ordering - that ) can only come after ( - then we have two options for every position, i.e., either put open parentheses or close parentheses. This means we can have a maximum of 2N combinations. Because of the ordering, the actual number will be less than 2N.
If you see the visual representation of Example-2 closely you will realize that, in the worst case, it is equivalent to a binary tree, where each node will have two children. This means that we will have 2N leaf nodes and 2N-1 intermediate nodes. So the total number of elements pushed to the queue will be 2N + 2N-1, which is asymptotically equivalent to O(2N). While processing each element, we do need to concatenate the current string with ( or ). This operation will take O(N), so the overall time complexity of our algorithm will be O(N*2N). This is not completely accurate but reasonable enough to be presented in the interview.
The actual time complexity ( O(4n/√n) ) is bounded by the Catalan number and is beyond the scope of a coding interview. See more details here.
Space complexity
All the additional space used by our algorithm is for the output list. Since we can’t have more than O(2N) combinations, the space complexity of our algorithm is O(N*2N).
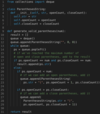
Unique Generalized Abbreviations
Given a word, write a function to generate all of its unique generalized abbreviations.
Generalized abbreviation of a word can be generated by replacing each substring of the word by the count of characters in the substring. Take the example of “ab” which has four substrings: “”, “a”, “b”, and “ab”. After replacing these substrings in the actual word by the count of characters we get all the generalized abbreviations: “ab”, “1b”, “a1”, and “2”.
Example 1
Input: “BAT”
Output: “BAT”, “BA1”, “B1T”, “B2”, “1AT”, “1A1”, “2T”, “3”
Example 2
Input: “code”
Output: “code”, “cod1”, “co1e”, “co2”, “c1de”, “c1d1”, “c2e”, “c3”, “1ode”, “1od1”, “1o1e”, “1o2”, “2de”, “2d1”, “3e”, “4”
This problem follows the Subsets pattern and can be mapped to Balanced Parentheses. We can follow a similar BFS approach.
Let’s take Example-1 mentioned above to generate all unique generalized abbreviations. Following a BFS approach, we will abbreviate one character at a time. At each step we have two options:
- Abbreviate the current character, or
- Add the current character to the output and skip abbreviation.
Since we had two options for each character, we will have a maximum of 2N combinations. If you see the visual representation of Example-1 closely you will realize that it is equivalent to a binary tree, where each node has two children. This means that we will have 2N leaf nodes and 2N-1 intermediate nodes, so the total number of elements pushed to the queue will be 2N + 2N-1, which is asymptotically equivalent to O(2N). While processing each element, we do need to concatenate the current string with a character. This operation will take O(N), so the overall time complexity of our algorithm will be O(N*2N).
All the additional space used by our algorithm is for the output list. Since we can’t have more than O(2N) combinations, the space complexity of our algorithm is O(N*2N).

Evaluate Expression
Given an expression containing digits and operations (+, -, *), find all possible ways in which the expression can be evaluated by grouping the numbers and operators using parentheses.
Example 1
Input: “1+2*3”
Output: 7, 9
Explanation: 1+(2*3) => 7 and (1+2)*3 => 9
Example 2
Input: “2*3-4-5”
Output: 8, -12, 7, -7, -3
Explanation: 2*(3-(4-5)) => 8, 2*(3-4-5) => -12, 2*3-(4-5) => 7, 2*(3-4)-5 => -7, (2*3)-4-5 => 8
This problem follows the Subsets pattern and can be mapped to Balanced Parentheses. We can follow a similar BFS approach.
Let’s take Example-1 mentioned above to generate different ways to evaluate the expression.
- We can iterate through the expression character-by-character.
- we can break the expression into two halves whenever we get an operator (+, -, *).
- The two parts can be calculated by recursively calling the function.
- Once we have the evaluation results from the left and right halves, we can combine them to produce all results.
The time complexity of this algorithm will be exponential and will be similar to Balanced Parentheses. Estimated time complexity will be O(N*2N) but the actual time complexity ( O(4n/√n) ) is bounded by the Catalan number and is beyond the scope of a coding interview. See more details here.
The space complexity of this algorithm will also be exponential, estimated at O(2N) though the actual will be O(4n/√n).
The problem has overlapping subproblems, as our recursive calls can be evaluating the same sub-expression multiple times. To resolve this, we can use memoization and store the intermediate results in a HashMap. In each function call, we can check our map to see if we have already evaluated this sub-expression before. Here is the memoized version of our algorithm; please see highlighted changes:
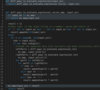
Structurally Unique Binary Search Trees
Given a number ‘n’, write a function to return all structurally unique Binary Search Trees (BST) that can store values 1 to ‘n’?
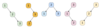
Example 1
Input: 2
Output: 2
Explanation: Here are all the structurally unique BSTs storing all numbers from 1 to 2:
Example 2
Input: 3
Output: 5
Explanation: Here are all the structurally unique BSTs storing all numbers from 1 to 3:
The time complexity of this algorithm will be exponential and will be similar to Balanced Parentheses. Estimated time complexity will be O(n*2n)but the actual time complexity ( O(4n/√n) ) is bounded by the Catalan number and is beyond the scope of a coding interview. See more details here.
The space complexity of this algorithm will be exponential too, estimated at O(2n), but the actual will be O(4n/√n).
Memoized version
Since our algorithm has overlapping subproblems, can we use memoization to improve it? We could, but every time we return the result of a subproblem from the cache, we have to clone the result list because these trees will be used as the left or right child of a tree. This cloning is equivalent to reconstructing the trees, therefore, the overall time complexity of the memoized algorithm will also be the same.
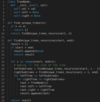
Count of Structurally Unique Binary Search Trees
Given a number ‘n’, write a function to return the count of structurally unique Binary Search Trees (BST) that can store values 1 to ‘n’.
Example 1
Input: 2
Output: 2
Explanation: As we saw in the previous problem, there are 2 unique BSTs storing numbers from 1-2.
Example 2
Input: 3
Output: 5
Explanation: There will be 5 unique BSTs that can store numbers from 1 to 5.
This problem is similar to Structurally Unique Binary Search Trees. Following a similar approach, we can iterate from 1 to ‘n’ and consider each number as the root of a tree and make two recursive calls to count the number of left and right sub-trees.
The time complexity of this algorithm will be exponential and will be similar to Balanced Parentheses. Estimated time complexity will be O(n*2n) but the actual time complexity O(4n/√n) ) is bounded by the Catalan number and is beyond the scope of a coding interview. See more details here.
The space complexity of this algorithm will be exponential too, estimated O(2n) but the actual will be O(4n/√n).
Our algorithm has overlapping subproblems as our recursive call will be evaluating the same sub-expression multiple times. To resolve this, we can use memoization and store the intermediate results in a HashMap. In each function call, we can check our map to see if we have already evaluated this sub-expression before.
The time complexity of the memoized algorithm will be O(n2), since we are iterating from ‘1’ to ‘n’ and ensuring that each sub-problem is evaluated only once. The space complexity will be O(n) for the memoization map.