Module 07: Rotational Motion Flashcards by carla klaasen

Lesson 7.1 Angular Quantities, Constant Angular Acceleration, and Rolling

What is translational motion?

Translational Motion: object’s center of mass plus rotational motion about the center

How well did you know this?

Not at all

Perfectly

Lesson 7.1 Angular Quantities, Constant Angular Acceleration, and Rolling

What is purely rotational motion?

Purely Rotational Motion:

All the points in the object move in a circle

The Center of the circles all lie on one line called the axis of rotation
The Axis of rotation is perpendicular to the center

All the points in an object rotate about a fixed axis moves in a circle

Straight-line drawn from the axis to any point in the object sweeps out the same angle in the same time interval.

How well did you know this?

Not at all

Perfectly

Lesson 7.1 Angular Quantities, Constant Angular Acceleration, and Rolling

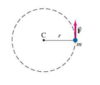
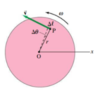
What is the angular position?

Angular Position: How far it rotates.

Specify the Θ of some particular line in the object (with respect to a reference line such as the x-axis)

A point in the object (P) moves through an angle Θ when it travels the distance (l) measured along the circumference of its circular path.

Use radians: Θ = l/r, where r = radius and l = arc length subtended by the angle

if l = r then Θ = 1 radians
Dimensionless, since it is a ratio of two lengths

How well did you know this?

Not at all

Perfectly

Lesson 7.1 Angular Quantities, Constant Angular Acceleration, and Rolling

How do radians and degrees relate to each other?

1 revolution = 360° = 2π
Radians to Degrees:

x° = rad/π * 180°

Degrees to Radians:

rad = π/180° * x°

How well did you know this?

Not at all

Perfectly

Lesson 7.1 Angular Quantities, Constant Angular Acceleration, and Rolling

What is angular displacement?

ΔΘ = Θ₂ - Θ₁

How well did you know this?

Not at all

Perfectly

Lesson 7.1 Angular Quantities, Constant Angular Acceleration, and Rolling

What is the angular velocity (ω)?

Average Angular Velocity:

ω = ΔΘ/Δt

Instantaneous Angular Velocity:

ω = lim_{(Δt - 0)} ΔΘ/Δt

Radians per second (rad/s)
Not all points in a rigid object rotate with the same angular velocity
Angular velocity is always perpendicular to the plane of rotation

How well did you know this?

Not at all

Perfectly

Lesson 7.1 Angular Quantities, Constant Angular Acceleration, and Rolling

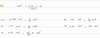
1. (I) Express the following angles in radians: (a) 45.0°, (b) 60.0°, (c) 90.0°, (d) 360.0°, and (e) 445°. Give as numerical values and as fractions of π.

How well did you know this?

Not at all

Perfectly

Lesson 7.1 Angular Quantities, Constant Angular Acceleration, and Rolling

What is the angular acceleration (α)?

Average Angular Acceleration:

α = Δω/Δt

Instantaneous Angular Acceleration:

α = lim_{(Δt - 0)} Δω/Δt

Acceleration same for all points
Radians per second squared (rad/s²)

How well did you know this?

Not at all

Perfectly

Lesson 7.1 Angular Quantities, Constant Angular Acceleration, and Rolling

What is linear velocity?

Each point has a linear velocity and acceleration

Can relate the linear quantities to angular quantities for a rigid object rotating about a fixed axis

If an object rotates with angular velocity, any point will have a linear velocity
Direction of linear velocity is tangent to the circular path
Magnitude of linear velocity:

v = Δl/Δt = r ΔΘ/Δt = rω

If the angular velocity of a rotating object changes, the object as a whole has an angular acceleration

How well did you know this?

Not at all

Perfectly

Lesson 7.1 Angular Quantities, Constant Angular Acceleration, and Rolling

What is linear acceleration?

If the angular velocity of a rotating object changes, the object as a whole has an angular acceleration

Linear acceleration is tangent to the point’s circular path

How well did you know this?

Not at all

Perfectly

Lesson 7.1 Angular Quantities, Constant Angular Acceleration, and Rolling

What is total linear acceleration?

Total Linear Acceleration of a point is the vector sum of two components:a = a_tan + a_R

a_R is the radial component - the “centripetal” acceleration and direction is towards the center of the circular path

How well did you know this?

Not at all

Perfectly

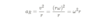
Lesson 7.1 Angular Quantities, Constant Angular Acceleration, and Rolling

What is the frequency of rotation?

Number of complete revolutions (rev) per second
One revolution = 2π radians
1 Hz = 1 rev / s

f = ω / 2π

How well did you know this?

Not at all

Perfectly

Lesson 7.1 Angular Quantities, Constant Angular Acceleration, and Rolling

What is rolling without slipping?

Rolling without slipping depends on static friction between object and ground

Friction is static because the object’s point of constant is at rest at each moment
Depends on both translational and rotational movement

v = rω

(Only is there is no slipping)

How well did you know this?

Not at all

Perfectly

Lesson 7.1 Angular Quantities, Constant Angular Acceleration, and Rolling

3. (I) A laser beam is directed at the Moon, 380,000 km from Earth. The beam diverges at an angle (Fig. 8–40) of 1.4 × 10^–5 rad. What diameter spot will it make on the Moon?

How well did you know this?

Not at all

Perfectly

Lesson 7.1 Angular Quantities, Constant Angular Acceleration, and Rolling

5. (II) The platter of the hard drive of a computer rotates at 7200 rpm (rpm = revolutions per minute = rev/min). (a) What is the angular velocity (rad/s) of the platter? (b) If the reading head of the drive is located 3.00 cm from the rotation axis, what is the linear speed of the point on the platter just below it? (c) If a single bit requires 0.50 m of length along the direction of motion, how many bits per second can the writing head write when it is 3.00 cm from the axis?

How well did you know this?

Not at all

Perfectly

Lesson 7.1 Angular Quantities, Constant Angular Acceleration, and Rolling

7. (II) (a) A grinding wheel 0.35 m in diameter rotates at 2200 rpm. Calculate its angular velocity in rad/s. (b) What are the linear speed and acceleration of a point on the edge of the grinding wheel?

How well did you know this?

Not at all

Perfectly

Lesson 7.1 Angular Quantities, Constant Angular Acceleration, and Rolling

9. (II) Calculate the angular velocity (a) of a clock’s second hand, (b) its minute hand, and (c) its hour hand. State in rad/s. (d) What is the angular acceleration in each case?

How well did you know this?

Not at all

Perfectly

Lesson 7.1 Angular Quantities, Constant Angular Acceleration, and Rolling

17. (I) An automobile engine slows down from 3500 rpm to 1200 rpm in 2.5 s. Calculate (a) its angular acceleration, assumed constant, and (b) the total number of revolutions the engine makes in this time.

How well did you know this?

Not at all

Perfectly

Lesson 7.1 Angular Quantities, Constant Angular Acceleration, and Rolling

19. (I) Pilots can be tested for the stresses of flying high-speed jets in a whirling “human centrifuge,” which takes 1.0 min to turn through 23 complete revolutions before reaching its final speed. (a) What was its angular acceleration (assumed constant), and (b) what was its final angular speed in rpm?

How well did you know this?

Not at all

Perfectly

Lesson 7.1 Angular Quantities, Constant Angular Acceleration, and Rolling

21. (II) A wheel 31 cm in diameter accelerates uniformly from 240 rpm to 360 rpm in 6.8 s. How far will a point on the edge of the wheel have traveled in this time?

How well did you know this?

Not at all

Perfectly

Lesson 7.1 Angular Quantities, Constant Angular Acceleration, and Rolling

23. (II) A small rubber wheel is used to drive a large pottery wheel. The two wheels are mounted so that their circular edges touch. The small wheel has a radius of 2.0 cm and accelerates at the rate of 7.2 rad/s², and it is in contact with the pottery wheel (radius 27.0 cm) without slipping. Calculate (a) the angular acceleration of the pottery wheel, and (b) the time it takes the pottery wheel to reach its required speed of 65 rpm.

How well did you know this?

Not at all

Perfectly

Lesson 7.2 Toque

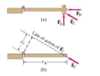
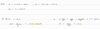
How does force relate to making an object roll?

Making an object start rolling requires a force
Direction important

F_A: perpendicular to the door

greater the magnitude, the faster it will open

F_B:

not open as quickly
$r_A$ is the lever arm

How well did you know this?

Not at all

Perfectly

Lesson 7.2 Toque

What is angular acceleration?

The angular acceleration is proportional to the (1) magnitude of the force and (2) directly proportional to the perpendicular distance from the axis of rotation to the line along which the force acts

“Distance” is the lever arm or moment arm (r)
Angular Acceleration is proportional to the product of the force times the lever arm
Product is the moment of the force and called the TORQUE (𝜏)

Hence, the angular acceleration is directly proportional to the net applied torque:

α ∝ 𝜏

Analogue with Newton’s Second Law

How well did you know this?

Not at all

Perfectly

Lesson 7.2 Toque

What is torque in relation to angular acceleration?

Product is the moment of the force and is called the TORQUE (𝜏)

Hence, the angular acceleration is directly proportional to the net applied torque:

α ∝ 𝜏

How well did you know this?

Not at all

Perfectly

# Lesson 7.2 Toque What is the lever arm and line of action?

**Lever Arm**: perpendicular distance from the axis of rotation to the line of action of the force (direction of the force) F_C: line along the direction of Fc (line of action) * Another line perpendicular to line of action * Magnitude of torque: *r_CF_C* Line of action of FD passes through the hinge, lever arm = 0 Hence, zero torque & zero angular acceleration

# Lesson 7.2 Toque What is the magnitude of the Torque about a Given Axis?

**𝜏 = r⊥F** * r⊥ is the lever arm (distance from axis is perpendicular to the line of action)

# Lesson 7.2 Toque How can torque be resolved through components?

Another way determine to torque is - Resolve the force into components parallel and perpendicular to the line

# Lesson 7.2 Toque What happens when there is more than one torque?

α proportional to the net torque * If all the torques are in the same direction: **sum of the torques** * If the torques are in opposite directions: **difference of the torques**

# Lesson 7.2 Toque What is the direction of torque?

* (CW) clockwise is negative * (CCW) counterclockwise is positive

# Lesson 7.2 Toque **25.** (II) Calculate the net torque about the axle of the wheel shown in Fig. 8–42. Assume that a friction torque of 0.60 m • N opposes the motion.

# Lesson 7.2 Toque **27.** (II) Two blocks, each of mass m, are attached to the ends of a massless rod which pivots as shown in Fig. 8–43. Initially the rod is held in the horizontal position and then released. Calculate the magnitude and direction of the net torque on this system when it is first released.

# Lesson 7.2 Toque **29.****\*** (II) Determine the net torque on the 2.0-m-long uniform beam shown in Fig. 8–45. All forces are shown. Calculate about (a) point C, the CM, and (b) point P at one end.

# Lesson 7.3 Rotational Dynamics How do translational motion and acceleration relate?

* Angular Acceleration and Net Torque: α ∝ Σ𝜏 * Corresponds to Newton’s Second Law: α ∝ ΣF **Translational Motion**: Acceleration is proportional to the net force and inversely proportional to the inertia of the object (m): **α = ΣF/m**

# Lesson 7.3 Rotational Dynamics Describe the force of a particle of mass revolved around a circle (r) at the end of a string:

* Force tangent to the center * Torque: **𝜏 = Fr** * Linear force (Newton’s Second Law): ΣF= ma * Tangential linear acceleration: a_tan =rα Thus: **F = ma = mrα** Torque: **𝜏 = rF = r(mrα) = mr²α** Direct relationship between Angular Acceleration and applied Torque mr² = *rotational inertia* of the particle and is the MOMENT of INERTIA

# Lesson 7.3 Rotational Dynamics What is the relationship between angular acceleration and torque?

Torque: **𝜏 = rF = r(mrα) = mr²α** * Direct relationship between Angular Acceleration and applied Torque * mr² = rotational inertia of the particle and is the MOMENT of INERTIA

# Lesson 7.3 Rotational Dynamics What is the **sum of torques** and **moment of inertia** of rotating rigid objects?

**Rotating rigid object** (Wheel as consisting of many particles located at various distances from the axis of rotation): Sum of various torques: Σ𝜏 = (Σmr²)α * α - the same for all the particles * Σmr²- the sum of the masses of each particle in the object \* square of the distance * Σmr²= m₁r₁² + m₂r₂² + m₃r₃² + ... Thus, **Moment of Inertia** (rotational inertia) I of the object: I = Σmr²= m₁r₁² + m₂r₂² + m₃r₃² + ... Combining the two equations: Σ𝜏 =Iα * The rotational equivalent of Newton’s Second Law * Valid of a fixed axis

# Lesson 7.3 Rotational Dynamics **31.** (I) Estimate the moment of inertia of a bicycle wheel 67 cm in diameter. The rim and tire have a combined mass of 1.1 kg. The mass of the hub (at the center) can be ignored (why?).

# Lesson 7.3 Rotational Dynamics **33.** (II) An oxygen molecule consists of two oxygen atoms whose total mass is 5.3 × 10^–26 kg and whose moment of inertia about an axis perpendicular to the line joining the two atoms, midway between them, is 1.9 × 10^–46 kg • m². From these data, estimate the effective distance between the atoms.

# Lesson 7.3 Rotational Dynamics **35.** (II) The forearm in Fig. 8–46 accelerates a 3.6-kg ball at 7.0 m/s2 by means of the triceps muscle, as shown. Calculate (a) the torque needed, and (b) the force that must be exerted by the triceps muscle. Ignore the mass of the arm.

# Lesson 7.3 Rotational Dynamics **37.** (II) A softball player swings a bat, accelerating it from rest to 2.6 rev/s in a time of 0.20 s. Approximate the bat as a 0.90-kg uniform rod of length 0.95 m, and compute the torque the player applies to one end of it.

# Lesson 7.3 Rotational Dynamics **39.** (II) Calculate the moment of inertia of the array of point objects shown in Fig. 8–47 about (a) the y axis, and (b) the x axis. Assume m = 2.2 kg, M = 3.4 kg, and the objects are wired together by very light, rigid pieces of wire. The array is rectangular and is split through the middle by the x axis. (c) About which axis would it be harder to accelerate this array?

# Lesson 7.3 Rotational Dynamics **41.** (II) A dad pushes tangentially on a small hand-driven merry-go-round and is able to accelerate it from rest to a frequency of 15 rpm in 10.0 s. Assume the merry-go-round is a uniform disk of radius 2.5 m and has a mass of 560 kg, and two children (each with a mass of 25 kg) sit opposite each other on the edge. (a) Calculate the torque required to produce the acceleration, neglecting frictional torque. (b) What force is required at the edge?

# Lesson 7.3 Rotational Dynamics **43.** (II) Let us treat a helicopter rotor blade as a long thin rod, as shown in Fig. 8–49. (a) If each of the three rotor helicopter blades is 3.75 m long and has a mass of 135 kg, calculate the moment of inertia of the three rotor blades about the axis of rotation. (b) How much torque must the motor apply to bring the blades from rest up to a speed of 6.0 rev/s in 8.0 s?

# Lesson 7.4 Rotational Kinetic Energy What is **rotational kinetic energy**?

* Rotational Objects (rigid rotating objects) * Joules * Total kinetic energy is the sum of the energies: KE = Σ(1/2mv²) = Σ(1/2mr²ω²) = 1/2(Σmv²)ω² Since I = Σmr² KE_r = 1/2Iω²

# Lesson 7.4 Rotational Kinetic Energy What type of kinetic energy does an object while its CM undergoes translational motion?

Object while its CM undergoes translational motion will have both translational and rotational kinetic energy: **KE = 1/2Mv²_CM + 1/2I_CMω²** * M = total mass * v²_CM = linear velocity of the center of the mass * I_CM= Moment of Inertia * ω = Angular velocity

# Lesson 7.4 Rotational Kinetic Energy What is to work done by torque?

* Work done on an object rotating about a fixed axis * Work: W = FΔl * Small Angle: ΔΘ = Δl/r Hence, W = FΔl = W = FrΔΘ * Torque: 𝜏 = rF Then, W = 𝜏ΔΘ Power(Rate of Work): **P = W/Δt = 𝜏ΔΘ/Δt = 𝜏ω** * Similar to the translational version (P=Fv)

# Lesson 7.4 Rotational Kinetic Energy **49.** (I) An automobile engine develops a torque of 265 m • N at 3350 rpm. What is the horsepower of the engine?

# Lesson 7.4 Rotational Kinetic Energy **51.** (I) Calculate the translational speed of a cylinder when it reaches the foot of an incline 7.20 m high. Assume it starts from rest and rolls without slipping.

# Lesson 7.4 Rotational Kinetic Energy **53.** (II) Estimate the kinetic energy of the Earth with respect to the Sun as the sum of two terms, (a) that due to its daily rotation about its axis, and (b) that due to its yearly revolution about the Sun. [Assume the Earth is a uniform sphere with mass = 6.0 × 10²⁴ kg, radius = 6.4 × 10⁶ m, and is 1.5 × 10⁸ km from the Sun.]

# Lesson 7.4 Rotational Kinetic Energy **55.** (II) A merry-go-round has a mass of 1440 kg and a radius of 7.50 m. How much net work is required to accelerate it from rest to a rotation rate of 1.00 revolution per 7.00 s? Assume it is a solid cylinder.

# Lesson 7.4 Rotational Kinetic Energy **57.** (II) A ball of radius r rolls on the inside of a track of radius R (see Fig. 8–53). If the ball starts from rest at the vertical edge of the track, what will be its speed when it reaches the lowest point of the track, rolling without slipping?

# Lesson 7.5 Angular Momentum What is **Angular Momentum** (L)?

Linear momentum: *p=mv* Symmetrical object rotating about a fixed axis through the CM: *L=Iω* SI units: kg \* m²/s

# Lesson 7.5 Angular Momentum What is Newton’s Second Law for Rotation?

Σ𝜏 = ΔL / Δt * Σ𝜏 = net torque * ΔL = Change in Angular Momentum * Σ𝜏 = Iα is a special case where the moment of inertia is constant

# Lesson 7.5 Angular Momentum What is the conservation of angular momentum?

The total angular momentum of a rotating object remains constant if the net torque acting on it is zero * If there is zero torque, the object is rotating about a fixed axis: *Iω = I₀ω₀ = constant*

# Lesson 7.5 Angular Momentum **61.** (I) (a) What is the angular momentum of a 2.8-kg uniform cylindrical grinding wheel of radius 28 cm when rotating at 1300 rpm? (b) How much torque is required to stop it in 6.0 s?

# Lesson 7.5 Angular Momentum **63.** (II) A nonrotating cylindrical disk of moment of inertia I is dropped onto an identical disk rotating at angular speed w. Assuming no external torques, what is the final common angular speed of the two disks?

# Lesson 7.5 Angular Momentum **65.** (II) A figure skater can increase her spin rotation rate from an initial rate of 1.0 rev every 1.5 s to a final rate of 2.5 rev/s. If her initial moment of inertia was 4.6 kg • m², what is her final moment of inertia? How does she physically accomplish this change?

# Lesson 7.5 Angular Momentum **67.** (II) A person of mass 75 kg stands at the center of a rotating merry-go-round platform of radius 3.0 m and moment of inertia 820 kg • m². The platform rotates without friction with angular velocity 0.95 rad/s. The person walks radially to the edge of the platform. (a) Calculate the angular velocity when the person reaches the edge. (b) Calculate the rotational kinetic energy of the system of platform plus person before and after the person’s walk.

# Lesson 7.5 Angular Momentum **69.** (II) A 4.2-m-diameter merry-go-round is rotating freely with an angular velocity of 0.80 rad/s. Its total moment of inertia is 1360 kg • m². Four people standing on the ground, each of mass 65 kg, suddenly step onto the edge of the merry-go-round. (a) What is the angular velocity of the merry-go-round now? (b) What if the people were on it initially and then jumped off in a radial direction (relative to the merry-go-round)?

**b**. The angular velocity of the merry-go-round will stay the same because the people are jumping in the radial direction, so along or “with” the curved path of the merry-go-round, so they will not provide any resistant force against the movement of the merry-go-round, so its angular velocity will remain the same as before the people stepped onto the merry-go-round.

# Quiz 7.2 A car is traveling along a freeway at 65 mph. What is the linear speed, relative to the highway, of each of the following points on one of its tires? * *(a)** the highest point on the tire * *(b)** the lowest point on a tire * *(c)** the center of the tire

**(a)** v = 2rω = 130 mph (r = 2R) **(b)** v = 0 = 65 mph (r = R) **(c)** v = rω = (r = 0)

# Quiz 7.2 A chicken is running in a circular path with an angular speed of 1.52 rad/s. How long does it take the chicken to complete one revolution? 1. 4.13 s 2. 118 s 3. 4.77 s 4. 8.26 s 5. 2.07 s

1. 4.13 s

# Quiz 7.2 Suppose a uniform solid sphere of mass M and radius R rolls without slipping down an inclined plane starting from rest. The linear velocity of the sphere at the bottom of the incline depends on 1. the radius of the sphere. 2. both the mass and the radius of the sphere. 3. the mass of the sphere. 4. neither the mass nor the radius of the sphere.

4. neither the mass nor the radius of the sphere

# Quiz 7.2 At a certain instant, a compact disc is rotating at 210 rpm. What is its angular speed in rad/s? 1. 660 rad/s 2. 69 rad/s 3. 22 rad/s 4. 45 rad/s 5. 11 rad/s

3. 22 rad/s

# Quiz 7.2 An electrical motor spins at a constant 2695.0. If the rotor radius is 7.165 cm, what is the linear acceleration of the edge of the rotor? 1. 281.6 m/s² 2. 5707 m/s² 3. 28.20 m/s² 4. 572,400 m/s²

2. 5707 m/s²

# Quiz 7.2 What is the angular speed, in rad/s, of a flywheel turning at 813.0 rpm? 1. 13.53 rad/s 2. 95.33 rad/s 3. 85.14 rad/s 4. 63.84 rad/s

3. 85.14 rad/s

# Quiz 7.2 Through how many degrees does a 33 rpm turntable rotate in 0.32 s? 1. 63° 2. 46° 3. 74° 4. 35°

1. 63°

# Quiz 7.2 A bicycle wheel has an outside diameter of 66 cm. Through what distance does a point on the rim move as the wheel rotates through an angle of 70°?

The distance will be 40 cm.

# Quiz 7.2 Two equal-magnitude forces are applied to a door at the doorknob. The first force is applied perpendicular to the door, and the second force is applied at 30° to the plane of the door. Which force exerts the greater torque about the door hinge? 1. the second force (applied at an angle) 2. the first force (applied perpendicular to the door) 3. Both forces exert zero torque. 4. Both forces exert equal non-zero torques.

2. the first force (applied perpendicular to the door)

# Quiz 7.2 An artificial satellite in a low orbit circles the earth every 98 minutes. What is its angular speed in rad/s?

The angular speed is 1.1×10^-3 rad/s

# Quiz 7.2 As shown in the figure, a given force is applied to a rod in several different ways. In which case is the torque about the pivot P due to this force the greatest? 3 2 1 5 4

# Quiz 7.2 Consider a solid uniform sphere of radius R and mass M rolling without slipping. Which form of its kinetic energy is larger, translational or rotational? 1. Translational kinetic energy is larger. 2. Rotational kinetic energy is larger. 3. You need to know the speed of the sphere to tell. 4. Both are equal.

1. Translational kinetic energy is larger

# Quiz 7.2 A solid sphere, solid cylinder, and a hollow pipe all have equal masses and radii. If the three of them are released simultaneously at the top of an inclined plane and do not slip, which one will reach the bottom first? 1. sphere 2. pipe 3. cylinder 4. The pipe and cylinder arrive together before the sphere. 5. They all reach the bottom at the same time.

1. sphere

# Quiz 7.2 Express the angular speed of an old 33 1/3 rpm LP in rad/s.

# Quiz 7.2 When Mary is 3.00 m from the center of a merry-go-round, her tangential speed is a constant 1.88 m/s. * *(a)** What is her angular speed in rad/s? * *(b)** What is the magnitude of her linear acceleration?

**Part B:** ## Footnote Linear acceleration = a_tan+ a_radial a_tan = Since the tangential speed is constant, the tangential acceleration is zero a_radial = w²r = 1.18 rad/s² Therefore, Linear acceleration = 0 + 1.18 rad/s² = **1.18 m/s²**

# Module 07 Exam (1) A solid sphere, solid cylinder, and a hollow pipe all have equal masses and radii. If the three of them are released simultaneously at the top of an inclined plane and do not slip, which one will reach the bottom first? 1. sphere 2. cylinder 3. They all reach the bottom at the same time. 4. pipe 5. The pipe and cylinder arrive together before the sphere.

1. sphere

# Module 07 Exam When you ride a bicycle, in what direction is the angular velocity of the wheels? 1. up 2. to your left 3. backwards 4. forwards 5. to your right

2. to your left

# Module 07 Exam The sun subtends an angle of 0.00928 rad when viewed from the surface of the earth, and its distance from Earth is 1.5 × 10¹¹ m. What is the diameter of the sun?

=(9.28×10^-3rad)(1.5×10¹¹m) =**1.4×10⁹m**

# Module 07 Exam Through how many degrees does a 33 rpm turntable rotate in 1. 74° 2. 46° 3. 35° 4. 63°

4. 63°

# Module 07 Exam Express the angular speed of an old 33 1/3 rpm LP in rad/s.

3.5 ^rad/_sec

# Module 07 Exam A cylinder of radius 8.0 cm rolls 20 cm in 5.0 s without slipping. Through how many degrees does the cylinder turn during this time?

# Module 07 Exam A bicycle wheel has an initial angular speed of 7.2 rad/s. After turning through one-half of a revolution, the angular speed is reduced to 2.2 rad/s. If the angular acceleration of the wheel was constant during the motion, how long will it take the wheel to make the one-half revolution?

# Module 07 Exam How long does it take for a rotating object to speed up from 15.0 rad/s to 33.3 rad/s if it has a uniform angular acceleration of 3.45 rad/s²? 1. 10.6 s 2. 4.35 s 3. 5.30 s 4. 9.57 s 5. 63.1 s

3. 5.30 s

# Module 07 Exam A machinist turns on the power on to a grinding wheel at time t = 0 s. The wheel accelerates uniformly from rest for 10 s and reaches the operating angular speed of 96 rad/s. The wheel is run at that angular velocity for 40 s and then power is shut off. The wheel slows down uniformly at 1.5 rad/s² until the wheel stops. For how long a time after the power is shut off does it take the wheel to stop? 1. 70 s 2. 64 s 3. 66 s 4. 68 s 5. 62 s

2. 64 s

# Module 07 Exam A centrifuge in a medical laboratory rotates at a rotational speed of 3600 rev/min. When switched off, it makes 50 complete turns at a constant angular acceleration before coming to rest. * *(a)** What was the magnitude of the angular acceleration of the centrifuge as it slowed down? * *(d)** How long did it take for the centrifuge to come to rest after being turned off?

**(a)** The angular acceleration is approximately 230rad/s² **(b)** The centrifuge takes approximately 1.7 seconds to come to rest

# Module 07 Exam In the figure, a weightlifter's barbell consists of two identical small but dense spherical weights, each of mass 50 kg. These weights are connected by a thin 0.96-m rod with a mass of 24 kg. Find the moment of inertia of the barbell through the axis perpendicular to the rod at its center, assuming the two weights are small enough to be treated as point masses.

# Module 07 Exam A solid uniform disk of diameter 3.20 m and mass 42 kg rolls without slipping to the bottom of a hill, starting from rest. If the angular speed of the disk is 4.27 rad/s at the bottom, how high did it start on the hill? 1. 2.68 m 2. 3.14 m 3. 3.57 m 4. 4.28 m

3. 3.57 m

# Module 07 Exam A solid uniform ball with a mass of 125 g is rolling without slipping along the horizontal surface of a table with a speed of 4.5 m/s when it rolls off the edge and falls towards the floor, 1.1 m below. What is the rotational kinetic energy of the ball just before it hits the floor? 1. 1.1 J 2. 0.73 J 3. This question cannot be answered without knowing the radius of the ball. 4. 0.51 J 5. 2.6 J

4. **0.51 J**

# Module 07 Exam A string is wrapped tightly around a fixed pulley that has a moment of inertia of 0.0352 kg ∙ m² and a radius of 12.5 cm. A mass of 423 g is attached to the free end of the string. With the string vertical and taut, the mass is gently released so it can descend under the influence of gravity. As the mass descends, the string unwinds and causes the pulley to rotate, but does not slip on the pulley. What is the speed of the mass after it has fallen through 1.25 m? 1. 3.94 m/s 2. 4.95 m/s 3. 1.97 m/s 4. 2.28 m/s 5. 2.00 m/s

3. **1.97 m/s**

# Module 07 Exam A string is wrapped tightly around a fixed frictionless pulley that has a moment of inertia of 0.0352 kg ∙ m² and a radius of 12.5 cm. The string is pulled away from the pulley with a constant force of 5.00 N, causing the pulley to rotate. What is the speed of the string after it has unwound 1.25 m if the string does not slip on the pulley? 1. 3.18 m/s 2. 4.95 m/s 3. 1.18m/s 4. 2.09 m/s 5. 2.36 m/s

5. **2.36 m/s** W_total = KE * Fx = 1/2 Iw²* * v = wr*

# Module 07 Exam An Atwood machine consists of a mass of 3.5 kg connected by a light string to a mass of 6.0 kg over a frictionless pulley with a moment of inertia of 0.0352 kg ∙ m²and a radius of 12.5 cm. If the system is released from rest, what is the speed of the masses after they have moved through 1.25 m if the string does not slip on the pulley? 1. 2.0 m/s 2. 4.0 m/s 3. 2.3 m/s 4. 6.0 m/s 5. 5.0 m/s

3. **2.3 m/s**

# Module 07 Exam The figure shows two blocks connected by a light cord over a pulley. This apparatus is known as an Atwood's machine. There is no slipping between the cord and the surface of the pulley. The pulley itself has negligible friction and it has a radius of 0.12 m and a mass of 10.3 kg. We can model this pulley as a solid uniform disk. At the instant that the heavier block has descended 1.5 m starting from rest, what is the speed of the lighter block?

# Module 07 Exam A solid uniform sphere is rolling without slipping along a horizontal surface with a speed of 5.5 m/s when it starts up a ramp that makes an angle of 25° with the horizontal. What is the speed of the sphere after it has rolled 3.0 m up as measured along the surface of the ramp? 1. 3.5 m/s 2. 1.9 m/s 3. 8.0 m/s 4. 4.0 m/s 5. 2.2 m/s

1. 3.5 m/s

# Module 07 Exam A solid uniform ball of mass 1.0 kg and radius 1.0 cm starts from rest and rolls down a 1.0-m high ramp. There is enough friction on the ramp to prevent the ball from slipping as it rolls down. * *(a)** What is the forward speed of the ball when it reaches the bottom of the ramp? * *(b)** What would be the forward speed of the ball if there were no friction on the ramp? * *(c)** Since the ball starts from the same height in both cases, why is the speed different?

**(c)** In part A, the object is not slipping meaning there is static friction and the motion depends on both translational and rotational movement. Therefore, the kinetic energy in part A is both translational and rotational. Comparatively, when there is slipping and the force of friction is zero, there is only translational motion, so the speeds are different in each case because the kinetic energy is made up of different components depending on how friction influences the movement of the ball.

# Module 07 Exam A force of 17 N is applied to the end of a 0.63-m long torque wrench at an angle 45° from a line joining the pivot point to the handle. What is the magnitude of the torque about the pivot point produced by this force? 1. 10.7 N ∙ m 2. 12.0 N ∙ m 3. 9.7 N ∙ m 4. 7.6 N ∙ m

4. 7.6 N ∙ m

# Module 07 Exam A particular motor can provide a maximum torque of 110 N ∙ m. Assuming that all of this torque is used to accelerate a solid, uniform, cylindrical flywheel of mass 10.0 kg and radius 3.00 m, how long will it take for the flywheel to accelerate from rest to 8.13 rad/s? 1. 4.03 s 2. 3.33 s 3. 2.83 s 4. 4.36 s

2. **3.33 s**

# Module 07 Exam A uniform rod is 2.0 m long. It is hinged to a wall at its left end, and held in a horizontal position at its right end by a vertical very light string, as shown in the figure. What is the angular acceleration of the rod at the moment after the string is released if there is no friction in the hinge? 1. 3.3 rad/s² 2. 11 rad/s² 3. It cannot be calculated without knowing the mass of the rod. 4. 15 rad/s² 5. 7.4 rad/s²

5. 7.4 rad/s²

# Module 07 Exam A uniform solid cylinder of mass 10 kg can rotate about a frictionless axle through its center O, as shown in the cross-sectional view in the figure. A rope wrapped around the outer radius R1 = 1.0 m exerts a force of magnitude F1 = 5.0 N to the right. A second rope wrapped around another section of radius R2 = 0.50 m exerts a force of magnitude F2 = 6.0 N downward. What is the angular acceleration of the cylinder? 1. 1.0 rad/s² 2. 0.80 rad/s² 3. 0.60 rad/s² 4. 0.40 rad/s²

4. 0.40 rad/s²

# Module 07 Exam The rotating systems shown in the figure differ only in that the two identical movable masses are positioned a distance r from the axis of rotation (left), or a distance r/2 from the axis of rotation (right). If you release the hanging blocks simultaneously from rest, and call tL the time taken by the block on the left and tR the time taken by the block on the right to reach the bottom, respectively, then 1. tL = tR. 2. tL \> tR. 3. tL

2. tL \> tR.

# Module 07 Exam A 385-g tile hangs from one end of a string that goes over a pulley with a moment of inertia of 0.0125 kg \* m² and a radius of 15.0 cm. A mass of 710 g hangs from the other end of the string. When the tiles are released, the larger one accelerates downward while the lighter one accelerates upward. The pulley has no friction in its axle and turns without the string slipping. What is the tension in the string on the side of the 710-g tile? 1. 6.87 N 2. 4.41 N 3. 3.68 N 4. 5.59 N 5. 9.77 N

**4.** 5.59 N

# Module 07 Exam A ballerina spins initially at 1.5 rev/s when her arms are extended. She then draws in her arms to her body and her moment of inertia becomes 0.88 kg ∙ m², and her angular speed increases to 4.0 rev/s. What was her initial moment of inertia?

# Module 07 Exam In a certain cyclotron, a proton of mass 1.67 × 10^-27 kg moves in a circle of diameter 1.6 m with an angular speed of 2.0 × 10⁶ rad/s. What is the angular momentum of the proton? 1. 1.8 × 10^-21 kg ∙ m²/s 2. 3.2 × 10^-21 kg ∙ m²/s 3. 1.3 × 10^-21 kg ∙ m²/s 4. 2.1 × 10^-21 kg ∙ m²/s

**4.** 2.1 × 10^-21 kg ∙ m²/s

# Module 07 Exam Three solid, uniform, cylindrical flywheels, each of mass 65.0 kg and radius 1.47 m, rotate independently around a common axis through their centers. Two of the flywheels rotate in one direction at 8.94 rad/s, but the other one rotates in the opposite direction at 3.42 rad/s. Calculate the magnitude of the net angular momentum of the system. 1. 975 kg ∙ m²/s 2. 940 kg ∙ m²/s 3. 1500 kg ∙ m²/s 4. 1020 kg ∙ m²/s

4. 1020 kg ∙ m²/s

# Module 07 Exam A uniform ball with diameter of 10 cm rolls without slipping on a horizontal tabletop. The moment of inertia of the ball about an axis through its center is 2.2 × 10^-3 kg ∙ m², and the translational speed of its center is 0.45 m/s. (a) What is its angular speed of the ball about its center of mass? (b) What is the rotational kinetic energy of the ball? (c) What is the ball's angular momentum about its center of mass?

# Module 07 Exam A solid wooden door, 90 cm wide by 2.0 m tall, has a mass of 35 kg. It is open and at rest. A small 500-g ball is thrown perpendicular to the door with a speed of 20 m/s and hits the door 60 cm from the hinged side, causing it to begin turning. The ball rebounds along the same line with a speed of 16.0 m/s relative to the ground. How much energy is lost during this collision? 1. 16 J 2. 30 J 3. 4.8 J 4. 15 J 5. 13 J

2. 30 J