Module 00: Introduction, Measurement, and Estimation Flashcards
Lesson 0.1 - Measurement, Uncertainty, Significant Figures Lesson 0.2 - Units, Standards, SI, and Converting Units
Lesson 0,1
What is the purpose of Physics?
The search for order in our observations of the natural world
Lesson 0,1
How do theories and observations relate to each other?
Observations - one side of the scientific process
Theories: explain and order the observations
Observations inspire the theory but it is based on the results of observations and experimentation
Lesson 0,1
How verifiable are theories, laws, and principles?
- No measurement is perfect, so exact confirmation is impossible
- Not possible to test all circumstances
Result: replace one theory with a new one if it yields better results
Lesson 0,1
What is a model and what is its purpose? `
Definition: kind of analogy or mental image of phenomena in terms of something already familiar
Purpose: Approximate mental or visual picture
Lesson 0,1
Difference between a theory and a model:
The theory is broader, more detailed than a model, and can be quantitatively tested.
Lesson 0,1
Define a Law:
Certain a concise but general statement about how nature behaves.
Descriptive: they do not say how nature should behave, but rather are meant to describe how nature cases possible
In general, a scientific law is the description of an observed phenomenon. It doesn’t explain why the phenomenon exists or what causes it. The explanation for a phenomenon is called a scientific theory.
How not Why
Lesson 0,1
How do you determine the percent uncertainty?
Ratio of the uncertainty to the measured values multiplied by 100.
for example: For 8.8 +- 0.1
= 0.1/8.8 * 100% = 1%
Lesson 0,1
What is the scientific figure of the following number: 32.21
4 sig figs
Lesson 0,1
What is the scientific figure of the following number: 0.062
2 (the zeros are placeholders)
Lesson 0,1
What is the scientific figure of the following number: 80
1 (the zero is a placeholder unless there is a decimal)
Lesson 0,1
What is the rule when multiplying or dividing scientific figures?
The Final result should have no more digits than the numerical value of the value with the fewest significant figures.
Lesson 0,1
What is the percent accuracy vs. the significant figures?
Use the significant figure rule but consider the % uncertainty too, and add an extra digit if it gives a more realistic estimate of uncertainty
Lesson 0.2
Why are standards (or units) important?
Makes sure there is a uniform method of measuring something
Lesson 0.2
What is the conversion factor from inches to meters?
1 inch = 2.54 centimeters
Lesson 0.2
What is the standard unit of mass?
kilograms (kg)
Lesson 0.2
What is the atomic mass in kg?
1 u = 1.6605 x 10-27kg
Lesson 0.2
What is SI (Systeme International or International System)?
- Standard length: meter
- Standard time: second
- Standard mass: kilograms
MKS system (meter-second-kilogram)
Lesson 0.2
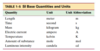
What are base and derivative quantities?
- Base quantity: defined in terms of a standard
- Derived quantities: all other quantities defined in terms of these seven base quantities
Lesson 0.2
What is an operational definition?
To define any quantity, whether base or derived, use a special rule or procedure.
Lesson 0.2
What is the conversion factor for feet to inches?
1 foot = 12 inches
Lesson 0.2
What are the three dimentions?
(1) mass, (2) length, and (3) time
Lesson 0.2
What are the steps of dimensional analysis?
Step 01: Identify what you know and what you need
Step 02: Set up conversion factors
Step 03: Cancel units and check
Step 04: Multiply the number
Practice Questions
- (I) How many significant figures do each of the following numbers have: (a) 214, (b) 81.60, (c) 7.03, (d) 0.03, (e) 0.0086, (f) 3236, and (g) 8700?
- 3 Significant Figures: 214
- 4 Significant Figures: 81.60
- 3 Significant Figures: 7.03
- 1 Significant Figure: 0.03
- 2 Significant Figures: 0.0086
- 4 Significant Figures: 3236
- 2 Significant Figures: 8700
Practice Questions
- (I) Write the following numbers in powers of 10 notation: (a) 1.156, (b) 21.8, (c) 0.0068, (d) 328.65, (e) 0.219, and (f) 444.
- 1.156 x 100
- 2.18 x 101
- 6.8 x 10-3
- 3.2865 x 102
- 2.19 x 10-1
- 4.44 x 102
Practice Questions
- (I) Write out the following numbers in full with the correct number of zeros: (a) 8.69 × 104, (b) 9.1 × 103, (c) 8.8 × 10–1, (d) 4.76 × 102, and (e) 3.62 × 10–5.
- 86900
- 9100
- 0.88
- 476
- 0.0000362
Practice Questions
- (II) The age of the universe is thought to be about 14 billion years. Assuming two significant figures, write this in powers of 10 in: (a) years (b) seconds
- 14,000,000,000 = 1.4 x 1010 years
- 4.4 x 1017 seconds
Practice Questions
- (II) What is the percent uncertainty in the measurement 5.48 ± 0.25 m?
4.6 %
Practice Questions
- (II) Time intervals measured with a stopwatch typically have an uncertainty of about 0.2 s, due to human reaction time at the start and stop moments. What is the percent uncertainty of a hand-timed measurement of (a) 5.5 s, (b) 55 s, (c) 5.5 min?
Attachment
Practice Questions
- Add (9.2 × 103 s) + (8.3 × 104 s) + (0.008 × 106 s).
= 9200s + 83000s + 8000s = 100200s = 1.002 x 105 = 1.00 x 105 s (Round to one digit since the value with the fewest significant figures, 0.008, only has one significant figure)
Practice Questions
- Multiply 3.079 × 102 m by 0.068 × 10–1 m, taking into account significant figures
307.9m * 0.0068m = 2.09372m = 2.1 m2 (Round to two digits since the value with the fewest significant figures, 0.0068, only has two significant figures)
Practice Questions
- (II) What, approximately, is the percent uncertainty for a measurement given as 1.57 m2?
Assuming that the uncertainty is one or a few units in the last digit specified, then the 1.57 will have an uncertainty of 1.57 0.01, so the measurement is likely between 1.56 and 1.58. Hence, the percent uncertainty is 0.6%
Lab Experiment: Introduction to Experimental Errors and Uncertainty
_____ describes the range of values within which the true value lies.
Uncertainty
Lab Experiment: Introduction to Experimental Errors and Uncertainty
Random error can be eliminated by performing multiple measurements on an object
True or False
False
Lab Experiment: Introduction to Experimental Errors and Uncertainty
Percent uncertainty is a measure of the _____ of a device
precision
Lab Experiment: Introduction to Experimental Errors and Uncertainty
What are true values?
True Values: Time, Distance, and Mass
- Important reference in scientific communities
- compared to known quantities for the purpose of understanding functions and processes in science
Lab Experiment: Introduction to Experimental Errors and Uncertainty
What are Error and Uncertainty?
Error: Difference between a measured value and true value
- Never perfect because measuring devices have limitations
Uncertainty: Parameter describing the range of values within which the true value lies
- Measured and uncertainty must have the same decimal places
- (measured value ± uncertainty range)proper units
Lab Experiment: Introduction to Experimental Errors and Uncertainty
What is a Systematic Error?
- Caused by improperly calibrated equipment and/or poor instruments
- results in consistently high or low values
- these errors are easily corrected by recalibrating devices, improving reading techniques, and applying a correction factor to previously recorded measurements
Lab Experiment: Introduction to Experimental Errors and Uncertainty
What is Random Error?
- Limitations of the measurements device and results in measurements
- results in unpredictable high and low values
- easy to detect statistically but impossible to correct or eliminate. However, performing multiple trials with the same device reduces the uncertainty created by this type of error.
Lab Experiment: Introduction to Experimental Errors and Uncertainty
What is the difference between Accuracy and Precision?
Accuracy:
- How close a measured value is to the true value
- Reported quantitatively as percent error
- Correlated to systematic error because measurements differ from the true value as a result of this error type
Precision:
- How close two or more independent measurements agree with each other
- Reported quantitatively as percent uncertainty
- correlated to random error because measurements vary from each other as a result of this error type
Lab Experiment: Introduction to Experimental Errors and Uncertainty
What is percent Error?
Increases as the difference between the measured value and expected value increases
Lab Experiment: Introduction to Experimental Errors and Uncertainty
What is Percent Uncertainty?
increases as the difference between independent measurements increases
Lab Experiment: Measurement Techniques
What are base, standard, and derived units?
Base Units: All measurements quantities
must be compared to standards understood and referenced throughout the scientific community
Standard Units: used for measurement in physics adhere to the System International (SI) framework established in 1960
Derived Units: further quantification of an object’s properties
Lab Experiment: Measurement Techniques
What is a meter stick?
- measure larger objects (like a motorcycle) and their properties (like the distance a motorcycle travels)
- lack the precision required for measuring smaller objects, such as a grain of sand
most meter sticks are in 1 mm or 0.1 mm graduations
Lab Experiment: Measurement Techniques
What is a Vernier Caliper?
- precision instrument consisting of a main scale containing one jaw and Vernier scale containing a second jaw that slides along the main scale
- The divisions on the Vernier scale indicate the least count or smallest quantity that the instrument can be resolve range between 0.1 mm (about the thickness of a sheet of paper) and 0.05 mm (about the size of the smallest cells in the human body)
- The span between the inner jaws measures the inside diameter between two surfaces. The distance between the outer jaws measures the exterior diameters and lengths of objects.
- Lastly, the depth probe measures interior depths and lengths of hollow or tubular objects like a soda can
- Before measuring an object, the jaws are closed and the alignment of the “0” mark on both the Vernier scale and main scale is noted to determine the zero error
- This number indicates the offset of the tool: any offset must be recorded and applied to future measurements. Exterior measurements of an object are taken with a Vernier caliper by first securing the object between the outer jaws. The position of the zero mark on the Vernier scale is noted relative to the main scale and rounded down to the next-smallest mark on the main scale. See Figure 3 for an illustration of the Vernier zero mark positioned between the 20 and 21 mm marks on the main scale. Each Vernier mark is then observed to determine which mark coincides (the Vernier coincidence) with a main scale mark. The number of this Vernier mark represents the fraction of the main scale division that must be added to the recorded measurement. See Figure 3 for an illustration of the Vernier 5 mark that coincides with the main scale 40 mark, resulting in a measurement of 20.50 mm.
- As with a meter stick, multiple trials are conducted when measuring objects with Vernier calipers to reduce random error.
Lab Experiment: Measurement Techniques
What are the volume formulas for:
(1) cube,
(2) sphere,
(3) cylinder
Cube: V=a3
Must measure one edge
Sphere: V = (4/3)πr3
Must measure the diameter
Cylinder: V=πr2h
Must measure the diameter and the height
Lab Experiment: Measurement Techniques
What is density?
🔬 Density: ratio of the mass of an object to the volume it occupies.
- Ratio is the compactness of the substance
- Intrinsic property (not vary with amount of a substance)
- useful to identify unknown materials by not 100% credited since difference substances are close to each other
- Units: g/cm3
Formula: ρ=m/V
