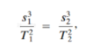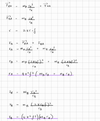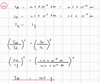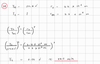Module 03: Motion and Gravitation

Question 1

Lesson 3.1: Uniform Circular Motion

What is uniform circular motion?

Answer 1

An object that moves in a circle at a constant speed (v)

1. Magnitude of the velocity remains constant
2. Direction of the velocity continuously changes as it goes around a circle

Question 2

Lesson 3.1: Uniform Circular Motion

Describe acceleration in a uniform circular motion:

Answer 2

Constantly accelerating:

• Defined as the rate of change of velocity, a change in direction of velocity is an acceleration, just like a change in magnitude.
• Constantly accelerating even when speed is constant

Question 3

Lesson 3.1: Uniform Circular Motion

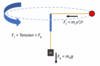
How do you calculate acceleration in Uniform Circular Motion (when t != 0)?

Answer 3

Question 4

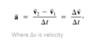
Lesson 3.1: Uniform Circular Motion

What is Centripetal (Radial) Acceleration?

Answer 4

🔬 Centripetal (Radial) Acceleration: (a_R)Directed along the radius, towards the centre of the circle

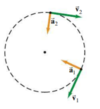
When ∆t is very small (approaching zero):

1. ∆l and ∆Θ are also very small
2. v2 will be almost parallel to v1 & ∆v will be essentially perpendicular to them (towards the centre of the circle)

Question 5

Lesson 3.1: Uniform Circular Motion

How do you calculate the magnitude of radial acceleration?

Answer 5

Question 6

Lesson 3.1: Uniform Circular Motion

What is the formula to determine radial acceleration?

Answer 6

Question 7

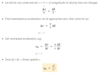
Lesson 3.1: Uniform Circular Motion

How does velocity change depending on speed and radius?

Answer 7

(1) Greater the speed (v) - the faster the velocity changes direction
(2) Larger the radius - the less rapidly the velocity changes direction

Question 8

Lesson 3.1: Uniform Circular Motion

Describe the acceleration and velocity vectors of uniform circular motion:

Answer 8

1. Acceleration vector points towards the center of the circle (v is constant)
2. Velocity vector points in the direction of motion (Tangential to the circle)

Perpendicular to each other

Question 9

Lesson 3.1: Uniform Circular Motion

What are frequencies and periods in a circular motion and how does it relate to speed?

Answer 9

Circular motion described in terms of …

1. Frequency (f): number of revolutions per second
2. Period (T): time required to complete one revolution

Relationship: T = 1/f

Speed travels a distance 2πr in one revolution:

Question 10

Lesson 3.1: Uniform Circular Motion

What is centripetal force and how is it calculated?

Answer 10

(According to Newton’s Second Law [ΣF = ma]) a net force is necessary to give it centripetal acceleration

Calculate the magnitude needed where ΣF_R = ma_R and where a_R = v²/r:

ΣF_R=ma_R=m(v²/r)

Net force directed towards the centre of the circle - called centripetal force

Question 11

Lesson 3.1: Uniform Circular Motion

What are the problem-solving steps to solve uniform circular motion questions?

Answer 11

1. Draw a FBD: show all forces (tension in a cord, gravity from Earth, normal force, friction) but not something that doesn’t belong (like centrifugal force)

2. Determine which forces act to provide the centripetal acceleration. The component that acts radially, towards or away from the centre of the circular path.
   Sum of these forces provides the centripetal acceleration: a_R = v²/r
3. Choose a convenient coordinate system
4. Apply Newton’s second law to the radial component: ΣF_R=ma_R=m(v²/r)

Question 12

Lesson 3.1: Uniform Circular Motion

Describe what happens when a car traveled around a curve?

Answer 12

• Feels like you are thrust outwards towards the right side door
• You move in a straight line, whereas the car moves in a curved path
• To make you go in the curved path, the seat (friction) and door of the car (direct contact) exert force on you
• The car also has a force exerted on it towards the centre of the curve if it is to move that curve

Question 13

Lesson 3.1: Uniform Circular Motion

What friction applies when a car is breaking?

Answer 13

• Wheels travel without slipping or sliding, the bottom of the tires rest against the road The friction force the road exerts is static
• If static friction is less than mv²/r and the car skid out of control = friction force becomes kinetic friction (smaller than static friction)
• Worse when the wheels lock: (when rolling, static friction exists) tires slide and friction force (kinetic) is less
• The direction also changes:
  Static friction can point perpendicular to the velocity
  The force no longer points towards the centre of the circle, and car continues in a curved path

Question 14

Lesson 3.1: Uniform Circular Motion

How do banked curves help reduce the chance of skidding?

Answer 14

• Normal force exerted by a banked road (perpendicular to the road) will have a component towards the centre of the circle - reducing friction
• Given banking angle Θ, one speed for which no friction at all is required
• When the horizontal component of the normal force towards the centre of the curve, F_NsinΘ = to the force required to give the vehicle its centripetal acceleration:

F_NsinΘ = mv²/r

Question 15

Lesson 3.2: Law of Universal Gravitation

Describe the centripetal acceleration of the moon due to the Earth’s gravity:

Answer 15

Question 16

Lesson 3.2: Law of Universal Gravitation

How is the gravitational force related to the distance from Earth’s centre?

Answer 16

Question 17

Lesson 3.2: Law of Universal Gravitation

How does gravity relate to distance and the mass of an object?

Answer 17

Question 18

Lesson 3.2: Law of Universal Gravitation

What is the Law of Universal Gravitation?

Answer 18

🔬 Law of Universal Gravitation: Every particle in the universe attracts every other particle with a force that is proportional to the product of their masses and inversely proportional to the square of the distance between them.

Magnitude of Gravitational Force:

• m₁ and m₂ are masses, r is the distance, and G is the universal constant (measured experimentally)
• G = 6.67 * 10^-11 N*m²/kg²

Question 19

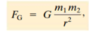
Lesson 3.2: Law of Universal Gravitation

How can you determine the Force of Gravity on an Object on the Earth’s Surface?

Answer 19

Question 20

How are satellites put into orbit?

Answer 20

• Put into orbit by accelerating it to a sufficiently high tangential speed
  
  • If its too high, it will escape
  • If its too low, it will return to earth
• Put into circular motion - because it requires the least takeoff speed

Question 21

How are satellites kept in space by their high speed?

Answer 21

Satellite in orbit is falling (accelerating) towards Earth, but its high tangential speed keeps it from hitting Earth

Needed acceleration = v²/r

Newton’s law of universal gravitation: (Apply Newton’s second law ΣF_R = ma_R in the radial direction)

• Height: r = r_E + h

Question 22

How does apparent weightlessness occur in an elevator?

Answer 22

If the elevator is in freefall

then a = -g and w=mg-mg=0

The bag appears to be weightless

Called = APPARENT WEIGHTLESSNESS

Question 23

What is Kepler’s First Law?

Answer 23

The path of each planet around the Sun is an ellipse with the Sun at one focus

Question 24

What is Kepler’s Second Law?

Answer 24

Each planet moves so that an imaginary line drawn from the Sun to the planet sweeps out equal areas in equal periods of time

Question 25

What is Kepler’s Third Law?

Answer 25

The ratio of squares of the period T of any two planets revolving around the Sun

• The mean distance equals the semimajor axis s]
• T1 and T2 are the periods, and s1 and s2 represent their mean distances from the Sun:

Question 26

Lesson 3.1 Questions

1. (I) A child sitting 1.20 m from the center of a merry-go-round moves with a speed of 1.10 m/s. Calculate (a) the centripetal acceleration of the child and (b) the net horizontal force exerted on the child (mass = 22.5 kg).

Answer 26

Question 27

Lesson 3.1 Questions

3. (I) A horizontal force of 310 N is exerted on a 2.0-kg ball as it rotates (at arm’s length) uniformly in a horizontal circle of radius 0.90 m. Calculate the speed of the ball.

Answer 27

Question 28

Lesson 3.1 Questions

5. (II) A 0.55-kg ball, attached to the end of a horizontal cord, is revolved in a circle of radius 1.3 m on a frictionless horizontal surface. If the cord will break when the tension in it exceeds 75 N, what is the maximum speed the ball can have?

Answer 28

Question 29

Lesson 3.1 Questions

7. (II) A car drives straight down toward the bottom of a valley and up the other side on a road whose bottom has a radius of curvature of 115 m. At the very bottom, the normal force on the driver is twice his weight. At what speed was the car traveling?

Answer 29

Question 30

Lesson 3.1 Questions

11. (II) How many revolutions per minute would a 25-m-diameter Ferris wheel need to make for the passengers to feel “weightless” at the topmost point?

Answer 30

Question 31

Lesson 3.1 Questions

13. (II) A proposed space station consists of a circular tube that will rotate about its center (like a tubular bicycle tire), Fig. 5–39. The circle formed by the tube has a diameter of 1.1 km. What must be the rotation speed (revolutions per day) if an effect nearly equal to gravity at the surface of the Earth (say, 0.90 g) is to be felt?

Answer 31

Question 32

Lesson 3.1 Questions

17. (II) Two blocks, with masses m_A and m_B, are connected to each other and to a central post by thin rods as shown in Fig. 5–41. The blocks revolve about the post at the same frequency f (revolutions per second) on a frictionless horizontal surface at distances r_A and r_B from the post. Derive an algebraic expression for the tension in each rod.

Answer 32

Question 33

Lesson 3.2 Questions

29. (I) At the surface of a certain planet, the gravitational acceleration g has a magnitude of 12.0 m/s². A 24.0-kg brass ball is transported to this planet. What is (a) the mass of the brass ball on the Earth and on the planet, and (b) the weight of the brass ball on the Earth and on the planet?

Answer 33

Question 34

Lesson 3.2 Questions

33. (II) Calculate the acceleration due to gravity on the Moon, which has radius 1.74 × 10⁶ m and mass 7.35 × 10²² kg.

Answer 34

Question 35

Lesson 3.2 Questions

35. (II) Given that the acceleration of gravity at the surface of Mars is 0.38 of what it is on Earth, and that Mars’ radius is 3400 km, determine the mass of Mars.

Answer 35

Question 36

Lesson 3.2 Questions

37. (II) A hypothetical planet has a mass 2.80 times that of Earth, but has the same radius. What is g near its surface?

Answer 36

Question 37

Lesson 3.2 Questions

39. (II) Calculate the effective value of g, the acceleration of gravity, at (a) 6400 m, and (b) 6400 km, above the Earth’s surface.

Answer 37

Question 38

Lesson 3.3 Questions

45. (I) A space shuttle releases a satellite into a circular orbit 780 km above the Earth. How fast must the shuttle be moving (relative to Earth’s center) when the release occurs?

Answer 38

Question 39

Lesson 3.3 Questions

47. (II) You know your mass is 62 kg, but when you stand on a bathroom scale in an elevator, it says your mass is 77 kg. What is the acceleration of the elevator, and in which direction?

Answer 39

Question 40

Lesson 3.3 Questions

49. (II) Calculate the period of a satellite orbiting the Moon, 95 km above the Moon’s surface. Ignore effects of the Earth. The radius of the Moon is 1740 km.

Answer 40

Question 41

Lesson 3.3 Questions

51. (II) What will a spring scale read for the weight of a 58.0-kg woman in an elevator that moves (a) upward with constant speed 5.0 m/s, (b) downward with constant speed 5.0 m/s, (c) with an upward acceleration 0.23 g, (d) with a downward acceleration 0.23 g, and (e) in free fall?

Answer 41

Question 42

Lesson 3.3 Questions

57. (I) Neptune is an average distance of 4.5 × 10⁹ km from the Sun. Estimate the length of the Neptunian year using the fact that the Earth is 1.50 × 10⁸ km from the Sun on average.

Answer 42

Question 43

Lesson 3.3 Questions

59. (I) Use Kepler’s laws and the period of the Moon (27.4 d) to determine the period of an artificial satellite orbiting very near the Earth’s surface.

Answer 43

Question 44

Lesson 3.3 Questions

61. (II) Our Sun revolves about the center of our Galaxy (m_G » 4 × 10⁴¹ kg) at a distance of about 3 × 10⁴ light-years [1 ly = (3.00 × 10⁸ m/s) • (3.16 × 10⁷ s/yr) • (1.00 yr)]. What is the period of the Sun’s orbital motion about the center of the Galaxy?

Answer 44

Question 45

Lesson 3.3 Questions

65. (II) Halley’s comet orbits the Sun roughly once every 76 years. It comes very close to the surface of the Sun on its closest approach (Fig. 5–45). Estimate the greatest distance of the comet from the Sun. Is it still “in” the solar system? What planet’s orbit is nearest when it is out there?

Answer 45

Question 46

Lab Experiment: Centripetal Acceleration

Define uniform circular motion:

Answer 46

Uniform Circular Motion: Object travels in a circular path at a constant speed, while their direction of velocity changes

Question 47

Lab Experiment: Centripetal Acceleration

What is centripetal acceleration?

Answer 47

Centripetal Acceleration: change in velocity - always points towards the center of the circular path traveled by the object.

Question 48

Lab Experiment: Centripetal Acceleration

What is the rotational axis?

Answer 48

Rotational Axis: Center point of the circular path, perpendicular to the plane of rotation

Question 49

Lab Experiment: Centripetal Acceleration

What is tangential velocity?

Question 50

Lab Experiment: Centripetal Acceleration

What is centripetal force?

Answer 50

Experienced by an object in uniform circular motion:

F_c = ma_c = mv² / r

Question 51

Lab Experiment: Centripetal Acceleration

How do you determine the speed for centripetal force?

Answer 51

• Angular Displacement: Angle, Θ, measured in radians, related to the degrees by the following conversion:

1 rev = 2π radians

• Arc Length (s): distance traced out in a circular path after creating a subtended angle, Θ.

s = Θr

• Circumference: (C) C = Θ_{1 rev}r = 2πr
• Speed determined using the circumference and the period:

v= displacement / time= 2πr / T = C / T

Question 52

Lab Experiment: Centripetal Acceleration

What is tension?

Answer 52

Tension: is a force transmitted through a string that allows a force to act over a distance

Tension = F_g = mg = F_c

Question 53

Determine the force providing the centripetal force for: a car making a turn

Answer 53

static friction between the car tire and the road

Question 54

Determine the force providing the centripetal force for child swinging around a pole.

Answer 54

the pulling force of the child’s arms

Question 55

Determine the force providing the centripetal force for a person sitting on a bench facing the center of a carousel

Answer 55

the normal force of the bench and the person’s back and/or the friction force of the bench seat and the person’s bottom

Question 56

Determine the force providing the centripetal force for a rock swinging on a string

Answer 56

d. the tension of the string

Question 57

Determine the force providing the centripetal force for the Earth Orbiting the Sun:

Answer 57

the gravitational force of the Sun on the Earth

Question 58

A car goes around a circular curve on a horizontal road at constant speed. What is the direction of the friction force on the car due to the road?

1. tangent to the curve opposite to the direction of the car’s motion
2. perpendicular to the curve inward
3. perpendicular to the curve outward
4. tangent to the curve in the forward direction
5. There is no friction on the car because its speed is constant.

Answer 58

2. perpendicular to the curve inward

Question 59

Module 03 Exam

When an object moves in uniform circular motion, the direction of its acceleration is

1. in the same direction as its velocity vector.
2. in the opposite direction of its velocity vector.
3. is directed away from the center of its circular path.
4. depends on the speed of the object.
5. is directed toward the center of its circular path.

Answer 59

5. is directed toward the center of its circular path

Question 60

Module 03 Exam

Two small objects, with masses m and M, are originally a distance r apart, and the magnitude of the gravitational force on each one is F. The masses are changed to 2m and 2M, and the distance is changed to 4r. What is the magnitude of the new gravitational force?

Answer 60

F/4

Question 61

Module 03 Exam

A spaceship is traveling to the Moon. At what point is it beyond the pull of Earth’s gravity?

1. when it is half-way there
2. when it gets above the atmosphere
3. It is never beyond the pull of Earth’s gravity.
4. when it is closer to the Moon than it is to Earth

Answer 61

3. It is never beyond the pull of Earth’s gravity

Question 62

Module 03 Exam

Planet A has twice the mass of Planet B. From this information, what can we conclude about the acceleration due to gravity at the surface of Planet A compared to that at the surface of Planet B?

1. The acceleration due to gravity on Planet A must be twice as great as the acceleration due to gravity on Planet B.
2. The acceleration due to gravity on Planet A is the same as the acceleration due to gravity on Planet B.
3. The acceleration due to gravity on Planet A must be four times as great as the acceleration due to gravity on Planet B.
4. The acceleration due to gravity on Planet A is greater than the acceleration due to gravity on Planet B, but we cannot say how much greater.
5. We cannot conclude anything about the acceleration due to gravity on Planet A without knowing the radii of the two planets.

Answer 62

5. We cannot conclude anything about the acceleration due to gravity on Planet A without knowing the radii of the two planets

Question 63

Module 03 Exam

Halley’s Comet is in a highly elliptical orbit around the sun. Therefore the orbital speed of Halley’s Comet, while traveling around the sun,

1. is constant.
2. decreases as it nears the Sun.
3. increases as it nears the Sun.
4. is zero at two points in the orbit.

Answer 63

3. increases as it nears the Sun

Question 64

Module 03 Exam

The curved section of a horizontal highway is a circular unbanked arc of radius 740 m. If the coefficient of static friction between this roadway and typical tires is 0.40, what would be the maximum safe driving speed for this horizontal curved section of highway?

Answer 64

54 m/s

Question 65

Module 03 Exam

A jet plane flying 600 m/s experiences an acceleration of 4.0 g when pulling out of a circular dive. What is the radius of curvature of the circular part of the path in which the plane is flying?

Answer 65

9200 m

Question 66

Module 03 Exam

One way that future space stations may create artificial gravity is by rotating the station. Consider a cylindrical space station 380 m in diameter that is rotating about its longitudinal axis. Astronauts walk on the inside surface of the space station. How long will it take for each rotation of the cylinder if it is to provide “normal” gravity for the astronauts?

Answer 66

28 s

Question 67

Module 03 Exam

A 2.0-kg ball is moving with a constant speed of 5.0 m/s in a horizontal circle whose diameter is 1.0 m. What is the magnitude of the net force on the ball?

Answer 67

100 N

Question 68

Module 03 Exam

A small 175-g ball on the end of a light string is revolving uniformly on a frictionless surface in a horizontal circle of diameter 1.0 m. The ball makes 2.0 revolutions every 1.0 s.

• *(a)** What are the magnitude and direction of the acceleration of the ball?
• *(b)** Find the tension in the string.

Answer 68

Question 69

Module 03 Exam

A future use of space stations may be to provide hospitals for severely burned persons. It is very painful for a badly burned person on Earth to lie in bed. In a space station, the effect of gravity can be reduced or even eliminated. How long should each rotation take for a doughnut-shaped hospital of 200-m radius so that persons on the outer perimeter would experience 1/10 the normal gravity of Earth?

Answer 69

1.5 min

Question 70

Module 03 Exam

A curved portion of highway has a radius of curvature of 65 m. As a highway engineer, you want to bank this curve at the proper angle for a steady speed of 22 m/s.

(a) What banking angle should you specify for this curve?
(b) At the proper banking angle, what normal force and what friction force does the highway exert on a 750-kg car going around the curve at the proper speed?

Answer 70

Since the curved portion of the highway is at the proper banking angle, there will be no force of friction if the car goes around the path.

Question 71

Module 03 Exam

What is the magnitude of the gravitational force that two small 7.00-kg balls exert on each other when they are 35.0 cm apart? (G = 6.67 × 10-11 N ∙ m2/kg2)

Answer 71

Question 72

Module 03 Exam

Two identical tiny balls of highly compressed matter are 1.50 m apart. When released in an orbiting space station, they accelerate toward each other at 2.00 cm/s2. What is the mass of each of them? (G = 6.67 × 10-11 N ∙ m2/kg2)

Answer 72

Question 73

Module 03 Exam

As a 70-kg person stands at the seashore gazing at the tides (which are caused by the Moon), how large is the gravitational force on that person due to the Moon? The mass of the Moon is 7.35 × 1022 kg, the distance to the Moon is 3.82 × 108 m, and G = 6.67 × 10-11 N ∙ m2/kg2.

Answer 73

0.0024 N

Question 74

Module 03 Exam

A very dense 1500-kg point mass (A) and a dense 1200-kg point mass (B) are held in place 1.00 m apart on a frictionless table. A third point mass is placed between the other two at a point that is 20.0 cm from B along the line connecting A and B. When the third mass is suddenly released, find the magnitude and direction (toward A or toward B) of its initial acceleration. (G = 6.67 × 10-11 N ∙ m2/kg2)

Answer 74

Question 75

Module 03 Exam

The mass of the Moon is 7.4 × 10²² kg, its radius is 1.74 × 10³ km, and it has no atmosphere. What is the acceleration due to gravity at the surface of the Moon? (G = 6.67 × 10-11 N ∙ m2/kg2)

Answer 75

1.6 m/s²

Question 76

Module 03 Exam

The mass of Pluto is 1.31 × 10²² kg and its radius is 1.15 × 10⁶ m. What is the acceleration of a freely-falling object at the surface of Pluto if it has no atmosphere? (G = 6.67 × 10-11 N ∙ m2/kg2)

Answer 76

0.661 m/s²

Question 77

Module 03 Exam

The earth has radius R. A satellite of mass 100 kg is in orbit at an altitude of 3R above the earth’s surface. What is the satellite’s weight at the altitude of its orbit?

Answer 77

61 N

Question 78

Module 03 Exam

A spherically symmetric planet has four times the earth’s mass and twice its radius. If a jar of peanut butter weighs 12 N on the surface of the Earth, how much would it weigh on the surface of this planet?

Answer 78

12 N

Question 79

Module 03 Exam

A 2.10-kg hammer is transported to the Moon. The radius of the Moon is 1.74 × 10⁶ m, its mass is 7.35 × 10²² kg, and G = 6.67 × 10-11 N ∙ m2/kg2. How much does the hammer weigh on Earth and on the Moon?

Answer 79

Question 80

Module 03 Exam

The captain of a spaceship orbiting planet X discovers that to remain in orbit at from the planet’s center, she needs to maintain a speed of 68m/s What is the mass of planet X? (G = 6.67 × 10-11 N ∙ m2/kg2)

Answer 80

2.8 × 10¹⁹ kg

Question 81

Module 03 Exam

You are the science officer on a visit to a distant solar system. Prior to landing on a planet you measure its diameter to be 1.8 × 107 m. You have previously determined that the planet orbits 2.9 × 1011 m from its star with a period of 402 earth days. Once on the surface you find that the acceleration due to gravity is 19.5 m/s2. What are the masses of (a) the planet and (b) the star? (G = 6.67 × 10-11 N ∙ m2/kg2)

Answer 81

(a) 2.4 kg × 10²⁵ kg,
(b) 1.2 kg × 1031 kg

Question 82

Module 03 Exam

In another solar system, a planet has a moon that is 4.0 × 10⁵ m in diameter. Measurements reveal that this moon takes 3.0 x 10⁵ s to make each orbit of diameter 1.8 × 10⁸ m. What is the mass of the planet? (G = 6.67 × 10-11 N ∙ m2/kg2)

Answer 82

4.8 × 10²⁴ kg

Question 83

Module 03 Exam

The International Space Station is orbiting at an altitude of about 370 km above the earth’s surface. The mass of the earth is 5.97 × 1024 kg, the radius of the earth is 6.38 × 106 m, and G = 6.67 × 10-11 N ∙ m2/kg2. Assume a circular orbit.

(a) What is the period of the International Space Station’s orbit?
(b) What is the speed of the International Space Station in its orbit?

Answer 83

Question 84

Module 03 Exam

A satellite of mass 500 kg orbits the earth with a period of 6,000 s. The earth has a mass of 5.97 × 1024 kg, a radius of 6.38 × 106 m, and G = 6.67 × 10-11 N ∙ m2/kg2.

(a) Calculate the magnitude of the earth’s gravitational force on the satellite.
(b) Determine the altitude of the satellite above the earth’s surface.

Answer 84

Question 85

Module 03 Exam

A large telescope of mass 8410 kg is in a circular orbit around the earth, making one revolution every 927 minutes. What is the magnitude of the gravitational force exerted on the satellite by the earth? (G = 6.67 × 10-11 N ∙ m2/kg2, Mearth = 6.0 × 1024 kg)

Answer 85

Question 86

Module 03 Exam

The innermost satellite of Jupiter orbits the planet with a radius of 422 × 103 km and a period of 1.77 days. What is the mass of Jupiter? (G = 6.67 × 10-11 N ∙ m2/kg2)

Answer 86

1.89 × 10²⁷ kg

Question 87

Module 03 Exam

It takes the planet Jupiter 12 years to orbit the sun once in a nearly circular orbit. Assuming that Jupiter’s orbit is truly circular, what is the distance from Jupiter to the sun, given that the distance from the earth to the sun is 1.5 × 1011 m?

Answer 87

7.9 × 10¹¹ m