Module 06: Oscillations

Question 1

Lesson 6.1 Simple Harmonic Motion (Part 1)

What is Periodic Motion?

Answer 1

🔬 Periodic Motion: Objects vibrates or oscillate back and forth, over the same path, with each oscillation taking the same amount of time

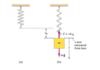
Ex: uniform coil spring

• Ignore mass
• Horizontally mounted
• Equilibrium Position: Spring’s natural length

Question 2

Lesson 6.1 Simple Harmonic Motion (Part 1)

What is the restoring force?

Answer 2

Restoring Force: Mass moved left/right, compressing the spring or stretching the string, the spring exerts a force on the mass that acts in the direction of returning mass to the equilibrium position

• Directly proportional to the displacement
• Opposite side as displacement

Question 3

Lesson 6.1 Simple Harmonic Motion (Part 1)

What is Hooke’s Law and its relation to Restoring Force?

Answer 3

• F = -kx*
• (Only use when the spring is not compressed to where it is touching or stretched more than max elasticity)*
• k - spring constant (N/m)
• Directly proportional with force needed to stretch spring

To stretch the spring in direction x, an external force must be exerted on free end of the spring with a magnitude of at least:

F_ext = +kx

Question 4

Lesson 6.1 Simple Harmonic Motion (Part 1)

What is displacement?

Answer 4

The distance x of the mass from the equilibrium point at any moment

Question 5

Lesson 6.1 Simple Harmonic Motion (Part 1)

What is amplitude?

Answer 5

Maximum distance (greatest distance from equilibrium point)

Question 6

Lesson 6.1 Simple Harmonic Motion (Part 1)

What is a cycle?

Answer 6

One cycle refers to the complete to-and-from motion from some point back to the same point

Question 7

Lesson 6.1 Simple Harmonic Motion (Part 1)

What is the period (T)?

Answer 7

Time required to complete one cycle

Question 8

Lesson 6.1 Simple Harmonic Motion (Part 1)

What is the frequency (f)?

Answer 8

Number of complete cycles per second Hertz (Hz), where 1 Hz = 1 cycle per second (s^-1)

f = 1/T

Question 9

Lesson 6.1 Simple Harmonic Motion (Part 1)

How does vertical oscillation compare to horizontal oscillation?

Answer 9

• Same as horizontal spring
• The length of vertical spring with a mass m on the end will be longer at equilibrium than when that same spring is horizontal.
• Equilibrium: ΣF = 0 = mg - kx₀

1. Spring stretches an extra amount x₀=mg/k to be in equilibrium
2. If x is measured from this new equilibrium position, can be used directly with the same value of k

Question 10

Lesson 6.1 Simple Harmonic Motion (Part 1)

What is the potential energy of a string?

Answer 10

Potential Energy is stored in a stretched or compressed string:

Elastic Potential Energy:

PE = 1/2kx²

Total Mechanical Energy (sum of kinetic and potential energies):

E = 1/2mv² + 1/2kx²

Question 11

Lesson 6.1 Simple Harmonic Motion (Part 1)

What is simple harmonic motion (SHM)?

Answer 11

Simple Harmonic Motion (SHM): Any oscillating system for which the net restoring force is directly proportional to the negative of the displacement (Also called a simple harmonic oscillator (SHO)).

• Only if friction is negligible - total mechanical energy stays constant
• As mass oscillates, the energy continuously changes from potential to kinetic energy

Question 12

Lesson 6.1 Simple Harmonic Motion (Part 1)

What is the total mechanical energy of a simple harmonic oscillator?

Answer 12

Total Mechanical Energy of a simple harmonic oscillator is proportional to the square of the amplitude

Question 13

Lesson 6.1 Simple Harmonic Motion (Part 1)

What happens in simple harmonic motion at the extreme points?

Answer 13

At extreme points: x = A and x= -A

• Energy is stored as potential energy
• Mass stops for an instant as it changes direction, so v=0 and

E = 1/2m(0)² + 1/2kA² = 1/2kA²

Question 14

Lesson 6.1 Simple Harmonic Motion (Part 1)

What happens in simple harmonic motion at the equilibrium points?

Answer 14

At equilibrium points: x=0

• Energy is exclusively kinetic
• Maximum speed during motion, so v_max and

E = 1/2mv_max² + 1/2k(0)² = 1/2mv_max²

Question 15

Lesson 6.1 Simple Harmonic Motion (Part 1)

What happens in simple harmonic motion at the intermediate points?

Answer 15

• Energy is partially kinetic and potential energy
• Energy is conserved

1/2mv² + 1/2kx² = 1/2kA²

Question 16

Lesson 6.1 Simple Harmonic Motion (Part 1)

What is velocity? (as a function of position)

Answer 16

Question 17

Lesson 6.2 Simple Harmonic Motion (Part 2)

What is the period of a Simple Harmonic Oscillator?

Answer 17

Period of a Simple Harmonic Oscillator found to depend on

1. stiffness of spring
2. Mass of the oscillator
3. Not depend on the amplitude

Increases alongside the mass and decreases alongside the spring constant

Force is directly proportional to the spring constant (so also acceleration)

Question 18

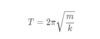
Lesson 6.2 Simple Harmonic Motion (Part 2)

What is the frequency of a Simple Harmonic Oscillator?

Answer 18

Question 19

Lesson 6.2 Simple Harmonic Motion (Part 2)

What is the time of a Simple Harmonic Oscillator?

Answer 19

Question 20

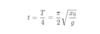
Lesson 6.2 Simple Harmonic Motion (Part 2)

How do you use derivatives to find distance, velocity, and acceleration?

Answer 20

where ω = 2πf

x(t) = Acos(ωt)

v(t) = x(t)’ = -Aω sin(ωt)

a(t) = x(t)’’ = -Aω² cos(ωt)

Question 21

Lesson 6.2 Simple Harmonic Motion (Part 2)

Describe position as a function of time:

Describe in terms of the frequency and period.

Answer 21

• Object’s position on the x axis: x = Acos θ
• Mass rotating with angular velocity ω, so θ = ωt, where theta is in radians. Then x = Acos ωt
• Angular velocity is in radians, so ω =2πf.

Therefore (in terms of frequency):

x = Acos(2πft)

And (in terms of the period):

x = Acos(2πt)/T

Question 22

Lesson 6.2 Simple Harmonic Motion (Part 2)

What is sinusoidal motion?

Answer 22

At x=Acos ωt

Assume oscillation starts from rest (v = 0) at its maximum displacement (x = A) at t = 0

• Same shape as cosine curve shown - shifted to the right by a quarter cycle
• Sine and cosine curves are being sinusoidal
• Simple harmonic motion is therefore also sinusoidal

Question 23

Lesson 6.2 Simple Harmonic Motion (Part 2)

Velocity and Acceleration curves as derivates of distance:

Answer 23

Question 24

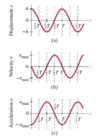
Lesson 6.2 Simple Harmonic Motion (Part 2)

Describe velocity as a function of distance:

Answer 24

• The magnitude of v is v_max sinθ
• And θ = ωt = 2­πft

Question 25

Lesson 6.2 Simple Harmonic Motion (Part 2)

What is maximum velocity?

Answer 25

Question 26

Lesson 6.2 Simple Harmonic Motion (Part 2)

Describe acceleration as a function of time:

Answer 26

• Max speed is larger if the amplitude is larger
• Newton’s second law gives the acceleration as a function of time:

Question 27

Lesson 6.2 Simple Harmonic Motion (Part 2)

What is maximum acceleration?

Answer 27

Question 28

Lesson 6.2 Simple Harmonic Motion (Part 2)

1. (I) If a particle undergoes SHM with amplitude 0.21 m, what is the total distance it travels in one period?

Answer 28

Question 29

Lesson 6.2 Simple Harmonic Motion (Part 2)

3. (II) An elastic cord is 61 cm long when a weight of 75 N hangs from it but is 85 cm long when a weight of 210 N hangs from it. What is the “spring” constant k of this elastic cord?

Answer 29

Question 30

Lesson 6.2 Simple Harmonic Motion (Part 2)

5. (II) A fisherman’s scale stretches 3.6 cm when a 2.4-kg fish hangs from it. (a) What is the spring stiffness constant and (b) what will be the amplitude and frequency of oscillation if the fish is pulled down 2.1 cm more and released so that it oscillates up and down?

Answer 30

Question 31

Lesson 6.2 Simple Harmonic Motion (Part 2)

7. (II) A mass m at the end of a spring oscillates with a frequency of 0.83 Hz. When an additional 780-g mass is added to m, the frequency is 0.60 Hz. What is the value of m?

Answer 31

Question 32

Lesson 6.2 Simple Harmonic Motion (Part 2)

9. (II) Figure 11–51 shows two examples of SHM, labeled A and B. For each, what is (a) the amplitude, (b) the frequency, and (c) the period?

Answer 32

Question 33

Lesson 6.2 Simple Harmonic Motion (Part 2)

11. (II) At what displacement of a SHO is the energy half kinetic and half potential?

Answer 33

Question 34

Lesson 6.2 Simple Harmonic Motion (Part 2)

13. (II) A 1.65-kg mass stretches a vertical spring 0.215 m. If the spring is stretched an additional 0.130 m and released, how long does it take to reach the (new) equilibrium position again?

Answer 34

Question 35

Lesson 6.2 Simple Harmonic Motion (Part 2)

15. (II) A 0.25-kg mass at the end of a spring oscillates 2.2 times per second with an amplitude of 0.15 m. Determine (a) the speed when it passes the equilibrium point, (b) the speed when it is 0.10 m from equilibrium, (c) the total energy of the system, and (d) the equation describing the motion of the mass, assuming that at t = 0, x was a maximum.

Answer 35

Question 36

Lesson 6.2 Simple Harmonic Motion (Part 2)

17. (II) If one oscillation has 3.0 times the energy of a second one of equal frequency and mass, what is the ratio of their amplitudes?

Answer 36

Question 37

Lesson 6.2 Simple Harmonic Motion (Part 2)

19. (II) A mass resting on a horizontal, frictionless surface is attached to one end of a spring; the other end is fixed to a wall. It takes 3.6 J of work to compress the spring by 0.13 m. If the spring is compressed, and the mass is released from rest, it experiences a maximum acceleration of 12 m/s². Find the value of (a) the spring constant and (b) the mass.

Answer 37

Question 38

Lesson 6.2 Simple Harmonic Motion (Part 2)

21. (II) At t = 0, an 885-g mass at rest on the end of a horizontal spring (k = 184 N/m) is struck by a hammer which gives it an initial speed of 2.26 m/s. Determine (a) the period and frequency of the motion, (b) the amplitude, (c) the maximum acceleration, (d) the total energy, and (e) the kinetic energy when x = 0.40A where A is the amplitude.

Answer 38

Question 39

Lesson 6.3 Simple Pendulum

What is a simple pendulum?

Answer 39

🔬 Simple Pendulum consists of a small object suspended from the end of a lightweight cord

• The cord does not stretch
• Mass can be ignored
• Negligible friction resembles the simple harmonic motion

Question 40

Lesson 6.3 Simple Pendulum

Describe the displacement of a pendulum along the arc given by s = lΘ.

Answer 40

Displacement (s) of the pendulum along the arc given by s = lΘ

• Θ is the angle (in radians) that the cord makes with the vertical
• l is the length of the cord

If the restoring force is proportional to s or Θ, the motion will be simple harmonic

Question 41

Lesson 6.3 Simple Pendulum

What is the restoring force in a simple pendulum? How does it change for small angles?

Answer 41

Restoring Force: net force on the bob = the components of the weight tangent to the arc

F = -mg sinΘ

• Opposite direction to the angular displacement
• Proportional to sine of Θ and not Θ itself - motion is not SHM
  
  • If Θ is very small, then sine of Θ is nearly equal to Θ

Hence, for very small angles:

F = -mgsin Θ ≈ -mgΘ

If s = lΘ or Θ = s/l:

F ≈ -mg/l * s

• Thus for small displacement, the motion is modelled as being approximately simple harmonic*
• The approximate equation fits Hooke’s Law (F=-kx) where s is in the place of x and k=mg/l

Question 42

Lesson 6.3 Simple Pendulum

What is the period of a small pendulum?

Answer 42

Question 43

Lesson 6.3 Simple Pendulum

Period of a Pendulum for the acceleration due to Gravity:

Answer 43

Question 44

Lesson 6.3 Simple Pendulum

What is the frequency of a small pendulum?

Answer 44

• The period and frequency do not depend on mass
• The period does not depend on the amplitude

Question 45

Lesson 6.3 Simple Pendulum

27. (I) A pendulum has a period of 1.85 s on Earth. What is its period on Mars, where the acceleration of gravity is about 0.37 that on Earth?

Answer 45

Question 46

Lesson 6.3 Simple Pendulum

28. (I) How long must a simple pendulum be if it is to make exactly one swing per second? (That is, one complete oscillation takes exactly 2.0 s.)

Answer 46

Question 47

Lesson 6.3 Simple Pendulum

29. (I) A pendulum makes 28 oscillations in exactly 50 s. What is its (a) period and (b) frequency?

Answer 47

Question 48

Lesson 6.3 Simple Pendulum

30. (II) What is the period of a simple pendulum 47 cm long (a) on the Earth, and (b) when it is in a freely falling elevator?

Answer 48

If the pendulum’s period is infinity on an elevator in freefall it will not oscillate back and forth and will be pushed into the opposite direction of gravity (so onto the ceiling), which would go on for infinity or until the elevator is no longer in freefall.

Question 49

Lesson 6.3 Simple Pendulum

31*. (II) Your grandfather clock’s pendulum has a length of 0.9930 m. If the clock runs slow and loses 21 s per day, how should you adjust the length of the pendulum?

Answer 49

If the pendulum’s period is infinity on an elevator in freefall it will not oscillate back and forth and will be pushed into the opposite direction of gravity (so onto the ceiling), which would go on for infinity or until the elevator is no longer in freefall.

Question 50

Lesson 6.4 Oscillations and Resonance

What is damped harmonic motion?

Answer 50

Damped Harmonic Motion - The amplitude of any real oscillating spring slowly decreases in time until the oscillations stop altogether

• Damping due to resistance in air and internal resistance
• Energy dissipated to thermal energy - decreases the amplitude
• SHM is easier to work with, so if sampling is not large, the oscillations can be thought of as SHM

Question 51

Lesson 6.4 Oscillations and Resonance

What are heavily damped systems?

Answer 51

No longer resemble SHM

Three common cases exist:

(A) Underdamped - the system makes several oscillations become coming to rest

(B) Critical Damping - The displacement reaches zero in a short time (shock absorbers in cars)

(C) Overdamped - Damping is so large there are no oscillations and the system take a long time to come to a rest

Question 52

Lesson 6.4 Oscillations and Resonance

What is force oscillation?

Answer 52

Force Oscillation: System has an external force applied to it which then has its own frequency

• Mass then oscillates at the external frequency of the external force:

Question 53

Lesson 6.4 Oscillations and Resonance

For forced oscillation with only light damping…

Answer 53

• The amplitude of oscillation is found to depend on the difference between f and f₀
• Maximum when the frequency of the external force equals the natural frequency of the system: f = f₀
• When the external frequency f is near natural frequency, f ≈ f₀, the amplitude can become large is damping is small

Question 54

Lesson 6.4 Oscillations and Resonance

What is resonance and resonance frequency?

Answer 54

Resonance: Effect of increasing amplitude at f = f₀

Resonant Frequency: Natural oscillation frequency f₀ of a system

Question 55

Quiz 6.2

A sewing machine needle moves in simple harmonic motion with a frequency of 2.5 Hz and an amplitude of 1.27 cm.

• *(a)** How long does it take the tip of the needle to move from the highest point to the lowest point in its travel?
• *(b)** How long does it take the needle tip to travel a total distance of 11.43 cm?

Answer 55

(a) 0.20 s

(b) 0.90 s

Question 56

Quiz 6.2

If a floating log is seen to bob up and down 15 times in 1.0 min as waves pass by you, what are the frequency and period of the wave?

Answer 56

Question 57

Quiz 6.2

A guitar string is set into vibration with a frequency of 512 Hz. How many oscillations does it undergo each minute?

1. 26.8
2. 30,700
3. 512
4. 1610
5. 8.53

Answer 57

the frequency is 512 1/s * 60s/1min = 30,700 oscillations/min (Option 2)

Question 58

Quiz 6.2

A point on the string of a violin moves up and down in simple harmonic motion with an amplitude of 1.24 mm and a frequency of 875 Hz.

• *(a)** What is the maximum speed of that point in SI units?
• *(b)** What is the maximum acceleration of the point in SI units?

Answer 58

(a) 6.82 m/s
(b) 3.75 × 10⁴ m/s2

Question 59

Quiz 6.2

The quartz crystal in a digital watch has a frequency of 32.8 kHz. What is its period of oscillation?

1. 95.8 µs
2. 30.5 µs
3. 15.3 µs
4. 0.191 ms
5. 9.71 µs

Answer 59

2. 30.5 µs

Question 60

Quiz 6.2

An object is undergoing simple harmonic motion of amplitude 2.3 m. If the maximum velocity of the object is 10 m/s, what is the object’s angular frequency?

1. 3.5 rad/s
2. 4.0 rad/s
3. 4.8 rad/s
4. 4.3 rad/s

Answer 60

4. 4.3 rad/s

Question 61

Quiz 6.2

A sewing machine needle moves up and down in simple harmonic motion with an amplitude of 1.27 cm and a frequency of 2.55 Hz. What are the (a) maximum speed and (b) maximum acceleration of the tip of the needle?

Answer 61

(a) 20.3 cm/s

(b) 326 cm/s²

Question 62

Quiz 6.2

An object that hangs from the ceiling of a stationary elevator by an ideal spring oscillates with a period T. If the elevator accelerates upward with acceleration 2g, what will be the period of oscillation of the object?

1. T
2. 4T
3. T/4
4. T/2
5. 2T

Answer 62

1. T

Question 63

Quiz 6.2

The figure shows a graph of the position x as a function of time t for a system undergoing simple harmonic motion. Which one of the following graphs represents the velocity of this system as a function of time?

Answer 63

graph b

Question 64

Quiz 6.2

A simple harmonic oscillator oscillates with frequency f when its amplitude is A. If the amplitude is now doubled to 2A, what is the new frequency?

1. 2f
2. f/4
3. 4f
4. f/2
5. f

Answer 64

5. f

Question 65

Quiz 6.2

The figure shows a graph of the position x as a function of time t for a system undergoing simple harmonic motion. Which one of the following graphs represents the acceleration of this system as a function of time?

Answer 65

graph a

Question 66

Quiz 6.2

The total mechanical energy of a simple harmonic oscillating system is

1. a minimum when it passes through the equilibrium point.
2. zero when it reaches the maximum displacement.
3. zero as it passes the equilibrium point.
4. a non-zero constant.
5. a maximum when it passes through the equilibrium point.

Answer 66

4. a non-zero constant

Question 67

Quiz 6.2

If a pendulum makes 12 complete swings in 8.0 s, what are its (a) frequency and (b) period?

Answer 67

(a) 1.5 Hz

(b) 0.67 s

Question 68

Quiz 6.2

If the frequency of a system undergoing simple harmonic motion doubles, by what factor does the maximum value of acceleration change?

1. 2
2. 4
3. 2/π

Answer 68

2. 4

Question 69

Quiz 6.2

A leaky faucet drips 40 times in 30.0 seconds.

What is the frequency of the dripping?

1. 0.63 Hz
2. 1.3 Hz
3. 1.6 Hz
4. 0.75 Hz

Answer 69

Frequency = Number # oscillations / time

Frequency = 40 / 30.0s = 1.3 Hz (Option 2)

Question 70

Module 6 Exam

A ball swinging at the end of a massless string, as shown in the figure, undergoes simple harmonic motion. At what point (or points) is the magnitude of the instantaneous acceleration of the ball the greatest?

A and B

B

A and C

C

A and D

Answer 70

A and D

Question 71

Module 6 Exam

Grandfather clocks are designed so they can be adjusted by moving the weight at the bottom of the pendulum up or down. Suppose you have a grandfather clock at home that runs fast. Which of the following adjustments of the weight would make it more accurate? (There could be more than one correct choice.)

1. Decrease the amplitude of swing by a small amount.
2. Lower the weight.
3. Add more mass to the weight.
4. Remove some mass from the weight.
5. Raise the weight.

Answer 71

2. Lower the weight

Question 72

Module 6 Exam

A pendulum of length L is suspended from the ceiling of an elevator. When the elevator is at rest the period of the pendulum is T. How does the period of the pendulum change when the elevator moves upward with constant velocity?

1. The period increases if the upward acceleration is more than g/2 but decreases if the upward acceleration is less than g/2.
2. The period becomes zero.
3. The period decreases.
4. The period does not change.
5. The period increases.

Answer 72

4. The period does not change.

Question 73

Module 6 Exam

A pendulum of length L is suspended from the ceiling of an elevator. When the elevator is at rest the period of the pendulum is T. How would the period of the pendulum change if the supporting chain were to break, putting the elevator into freefall?

1. The period decreases slightly.
2. The period does not change.
3. The period increases slightly.
4. The period becomes infinite because the pendulum would not swing.
5. The period becomes zero.

Answer 73

4. The period becomes infinite because the pendulum would not swing

Question 74

Module 6 Exam

A simple pendulum and a mass oscillating on an ideal spring both have period T in an elevator at rest. If the elevator now moves downward at a uniform 2 m/s, what is true about the periods of these two systems?

1. Both periods would remain the same.
2. Both periods would decrease.
3. The period of the pendulum would decrease but the period of the spring would stay the same.
4. The period of the pendulum would increase but the period of the spring would stay the same.
5. Both periods would increase.

Answer 74

1. Both periods would remain the same

Question 75

Module 6 Exam

If a floating log is seen to bob up and down 15 times in 1.0 min as waves pass by you, what are the frequency and period of the wave?

Answer 75

Frequency = num # oscillations / time = 15 / 60 sec = 0.25 Hz

Period = 1/f = 1/0.25 = 4 sec

Question 76

Module 6 Exam

The quartz crystal in a digital watch has a frequency of 32.8 kHz. What is its period of oscillation?

1. 9.71 µs
2. 0.191 ms
3. 30.5 µs
4. 95.8 µs
5. 15.3 µs

Answer 76

3. 30.5 µs

Question 77

Module 6 Exam

*11* A sewing machine needle moves in simple harmonic motion with a frequency of 2.5 Hz and an amplitude of 1.27 cm.

• *(a)** How long does it take the tip of the needle to move from the highest point to the lowest point in its travel?
• *(b)** How long does it take the needle tip to travel a total distance of 11.43 cm?

Answer 77

***********

Question 78

Module 6 Exam

If a pendulum makes 12 complete swings in 8.0 s, what are its (a) frequency and (b) period?

Answer 78

Frequency = num # oscillations / time = 12 / 8.0sec = 1.5 Hz

Period = 1/f =1 / 1.5Hz = 0.67sec

Question 79

Module 6 Exam

A point on the string of a violin moves up and down in simple harmonic motion with an amplitude of 1.24 mm and a frequency of 875 Hz.

• *(a)** What is the maximum speed of that point in SI units?
• *(b)** What is the maximum acceleration of the point in SI units?

Answer 79

(a) 6.82 m/s

(b) 3.75 × 10⁴ m/s²

Question 80

Module 6 Exam

The position of a cart that is oscillating on a spring is given by the equation x = (12.3 cm) cos[(1.26 s^-1)t]. When t = 0.805 s, what are the (a) velocity and (b) acceleration of the cart?

Answer 80

(a) -13.2 cm/s

(b) -10.3 cm/s²

Question 81

Module 6 Exam

An air-track cart is attached to a spring and completes one oscillation every 5.67 s in simple harmonic motion. At time t = 0.00 s the cart is released at the position x = +0.250 m. What is the position of the cart when t = 29.6 s?

1. x = 0.342 m
2. x = -0.218 m
3. x = 0.0461 m
4. x = 0.218 m
5. x = 0.210 m

Answer 81

3. x = 0.0461 m

Question 82

Module 6 Exam

An object is oscillating on a spring with a period of 4.60 s. At time t = 0.00 s the object has zero speed and is at x = 8.30 cm. What is the acceleration of the object at t = 2.50 s?

1. 14.9 cm/s²
2. 11.5 cm/s²
3. 0.784 cm/s²
4. 1.33 cm/s²
5. 0.00 cm/s²

Answer 82

1. 14.9 cm/s²

Question 83

Module 6 Exam

The position of an object that is oscillating on an ideal spring is given by x = (17.4 cm) cos[(5.46 s-1)t]. Write an expression for the acceleration of the particle as a function of time using the cosine function.

Answer 83

a = - (519 cm/s²) cos[(5.46 s^-1)t]

Question 84

Module 6 Exam

A 0.150-kg air track cart is attached to an ideal spring with a force constant (spring constant) of 3.58 N/m and undergoes simple harmonic oscillations. What is the period of the oscillations?

1. 1.14 s
2. 1.29 s
3. 2.57 s
4. 0.263 s
5. 0.527 s

Answer 84

2. 1.29 s

Question 85

Module 6 Exam

* 19 * A 1.15-kg beaker (including its contents) is placed on a vertical spring scale. When the system is sent into vertical vibrations, it obeys the equation y = (2.3 cm)cos(17.4 s^-1 t). What is the force constant (spring constant) of the spring scale, assuming it to be ideal?

Answer 85

(Possible Answer): 796.49 N/m

Question 86

Module 6 Exam

An object of mass m = 8.0 kg is attached to an ideal spring and allowed to hang in the earth’s gravitational field. The spring stretches 2.2 cm before it reaches its equilibrium position. If it were now allowed to oscillate by this spring, what would be its frequency?

1. 1.6 Hz
2. 0.28 x 10^-3 Hz
3. 0.52 Hz
4. 3.4 Hz

Answer 86

4. 3.4 Hz

Question 87

Module 6 Exam

A 2.0-kg block on a frictionless table is connected to two springs whose opposite ends are fixed to walls, as shown in the figure. The springs have force constants (springconstants) k1 and k2. What is the oscillation angular frequency of the block if k1 = 7.6 N/m and k2 = 5.0 N/m?

1. 3.5 rad/s
2. 0.40 rad/s
3. 0.56 rad/s
4. 2.5 rad/s

Answer 87

4. 2.5 rad/s

Question 88

Module 6 Exam

A block attached to an ideal spring of force constant (spring constant) 15 N/m executes simple harmonic motion on a frictionless horizontal surface. At time t = 0 s, the block has a displacement of -0.90 m, a velocity of -0.80 m/s, and an acceleration of +2.9 m/s2 . The mass of the block is closest to

1. 4.7 kg
2. 9.4 kg
3. 2.6 kg
4. 2.3 kg

Answer 88

1. 4.7 kg

Question 89

Module 6 Exam

* 23 * A 0.39-kg block on a horizontal frictionless surface is attached to an ideal spring whose force constant (spring constant) is 570 N/m. The block is pulled from its equilibrium position at x = 0.000 m to a displacement x = +0.080 m and is released from rest. The block then executes simple harmonic motion along the horizontal x-axis. When the position of the block is x = 0.057 m, its kinetic energy is closest to

1. 1 J.
2. 95 J.
3. 0 J.
4. 90 J.
5. 84 J.

Answer 89

Might be … 0.9 J

1/2kA² = 1/2kx² = 1/2mv²

Question 90

Module 6 Exam

An object of mass 6.8 kg is attached to an ideal spring of force constant (spring constant) 1720 N/m. The object is set into simple harmonic motion, with an initial velocity of v0 = 4.1 m/s and an initial displacement of x0 = 0.11 m. Calculate the maximum speed the object reaches during its motion.

Answer 90

Question 91

Module 6 Exam

A 0.50-kg box is attached to an ideal spring of force constant (spring constant) 20 N/m on a horizontal, frictionless floor. The box oscillates in simple harmonic motion and has a speed of 1.5 m/s at the equilibrium position.

• *(a)** What is the amplitude of vibration?
• *(b)** At what distance from the equilibrium position are the kinetic energy and the potential energy the same?

Answer 91

(a) 0.24 m (b) 0.17 m

Question 92

Module 6 Exam

A 0.50-kg object is attached to an ideal spring of spring constant (force constant) 20 N/m along a horizontal, frictionless surface. The object oscillates in simple harmonic motion and has a speed of 1.5 m/s at the equilibrium position. What are (a) the total energy and (b) the amplitude of vibration of the system?

Answer 92

(a) 0.56 J

(b) 0.24 m

Question 93

Module 6 Exam

What is the length of a simple pendulum with a period of 2.0 s?

1. 1.6 m
2. 20 m
3. 1.2 m
4. 0.87 m
5. 0.99 m

Answer 93

5. 0.99 m

Question 94

Module 6 Exam

* 28* A simple pendulum has a period T on Earth. If it were used on Planet X, where the acceleration due to gravity is 3 times what it is on Earth, what would its period be?

1. T/3
2. T
3. square 3 T
4. T/square 3
5. 3T

Question 95

Module 6 Exam

An astronaut has landed on Planet N-40 and conducts an experiment to determine the acceleration due to gravity on that planet. She uses a simple pendulum that is 0.640 m long and measures that 10 complete oscillations 26.0 s. What is the acceleration of gravity on Planet N-40?

1. 4.85 m/s²
2. 1.66 m/s²
3. 2.39 m/s²
4. 3.74 m/s²
5. 9.81 m/s²

Answer 95

4. 3.74 m/s²

Question 96

Module 6 Exam

An astronaut has landed on an asteroid and conducts an experiment to determine the acceleration of gravity on that asteroid. He uses a simple pendulum that has a period of oscillation of 2.00 s on Earth and finds that on the asteroid the period is 11.3 s. What is the acceleration of gravity on that asteroid?

1. 1.74 m/s²
2. 5.51 m/s²
3. 0.307 m/s²
4. 0.0544 m/s²
5. 1.66 m/s²

Answer 96

3. 0.307 m/s²