Module 05: Linear Momentum Flashcards
Lesson 5.1 Momentum and Its Conservation
What is Linear Momentum?
Linear Momentum of an object is defined as the product of its mass and its velocity (p)
p = mv
- Is a vector
- The direction of momentum is the direction of velocity
- Unit: kg*m/s
- More momentum - the harder it to stop something
Lesson 5.1 Momentum and Its Conservation
How do you calculate the total momentum of two objects before and after collision?
When we desire to calculate the total momentum of two objects before the collision, their total momentum after collision is zero.
m1u1 + m2u2 = 0
When two objects move in the exact direction, the total momentum before the collision is,
- Pbefore collision = m1u1 + m2u2
When two objects move in opposite directions, the total momentum before the collision is,
- Pbefore collision = m1u1 + -(m2u2)
- Pbefore collision = m1u1- m2u2
Lesson 5.1 Momentum and Its Conservation
How does Newton’s Second Law of Motion apply to collision and momentum?
Force needed to change momentum (increasing/decreasing or changing direction)
🔬 Newton’s Second Law of Motion: The Rate of change of momentum of an object is equal to the net force applied to it
F= Δp/Δt

Lesson 5.1 Momentum and Its Conservation
What is the Law of Conservation of Momentum?
Law of Conservation of Momentum:
The total momentum of an isolated system of objects remains constant
- Momentum is a conserved quantity - when there are no net external forces acting on it
- Hence, as long as there is no external force:
mAvA = mBvB = mAvA’ + mBvB‘
- Must keep time interval small - since nonconserved forces act in the real world
- Conserved as long as PA and PB are measured just before the collision and P’A and P’B just after
- Useful when dealing with simple systems (colliding objects and “explosions”)
Lesson 5.1 Questions
1. (I) What is the magnitude of the momentum of a 28-g sparrow flying with a speed of 8.4 m/s?

Lesson 5.1 Questions
3. (I) A 7150-kg railroad car travels alone on a level frictionless track with a constant speed of 15.0 m/s. A 3350-kg load, initially at rest, is dropped onto the car. What will be the car’s new speed?

Lesson 5.1 Questions
5. (II) Calculate the force exerted on a rocket when the propelling gases are being expelled at a rate of 1300 kg/s with a speed of 4.5 × 104 m/s.
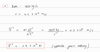
Lesson 5.1 Questions
7. (II) A child in a boat throws a 5.30-kg package out horizontally with a speed of 10.0 m/s, Fig. 7– 31. Calculate the velocity of the boat immediately after, assuming it was initially at rest. The mass of the child is 24.0 kg and the mass of the boat is 35.0 kg.

Lesson 5.2 Momentum and Its Conservation
What are the forces involved in a collision?
- During a collision of two objects - both objects are deformed because of large forces involved
- Collision: force each exerts on the other usually jumps from zero at the moment of constant to very large force - then returns to zero again
- The magnitude of the force that one object exerts on the other during a collision, as a function of time
- Time is very distinct and very small
- milliseconds for macroscopic collisions
Lesson 5.2 Momentum and Its Conservation
What is the net force of momentum?
Net force (based on Newton’s Second Law): equal to the rate of change of momentum
F = Δp / Δt
- where p = mv
Lesson 5.2 Momentum and Its Conservation
What is impulse?
Applies to each of the two objects in a collision
Impulse: Total change in momentum
- Used when t = small
- Not constant force
- Approximate force using the average force
- Units for impulse: Newton x second (N*s)
FΔt = Δp
Lesson 5.2 Momentum and Its Conservation
15. (I) A 0.145-kg baseball pitched at 31.0 m/s is hit on a horizontal line drive straight back at the pitcher at 46.0 m/s. If the contact time between bat and ball is 5.00 × 10–3 s, calculate the force (assumed to be constant) between the ball and bat.

Lesson 5.2 Momentum and Its Conservation
17. (II) A 12-kg hammer strikes a nail at a velocity of 7.5 m/s and comes to rest in a time interval of 8.0 ms. (a) What is the impulse given to the nail? (b) What is the average force acting on the nail?

Lesson 5.2 Momentum and Its Conservation
19. (II) A 125-kg astronaut (including space suit) acquires a speed of 2.50 m/s by pushing off with her legs from a 1900-kg space capsule. (a) What is the change in speed of the space capsule? (b) If the push lasts 0.600 s, what is the average force exerted by each on the other? As the reference frame, use the position of the capsule before the push. (c) What is the kinetic energy of each after the push?

Lesson 5.2 Momentum and Its Conservation
21. (II) A 95-kg fullback is running at 3.0 m/s to the east and is stopped in 0.85 s by a head-on tackle by a tackler running due west. Calculate (a) the original momentum of the fullback, (b) the impulse exerted on the fullback, (c) the impulse exerted on the tackler, and (d) the average force exerted on the tackler.

Lesson 5.3 Elastic Collisions
When is total kinetic energy conserved?
If two objects are very hard and no heat or energy is produced in the collision = Total Kinetic Energy before and after collision stays constant
Lesson 5.3 Elastic Collisions
What happens to energy the moment of collision?
The moment during contact = energy is stored momentarily in the form of Elastic Potential Energy.
Lesson 5.3 Elastic Collisions
What is an elastic collision?
Elastic Collision is where the total kinetic energy just before and after the collision stays constant
- At the atomic level, the collisions of atoms and molecules are often elastic
- When kinetic energy is not conserved, the total energy is always conserved
Lesson 5.3 Elastic Collisions
What is an inelastic collision?
Inelastic Collision is when the total kinetic energy is not conserved
- Kinetic energy is lost is changing into other forms of energy

Lesson 5.3 Elastic Collisions
Apply the Conservation Laws for Momentum and Kinetic Energy to elastic collisions:
- For v>0 the object is moving to the right (increasing x)
- For v<0 the object is moving to the left (decreasing value of x)
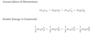
Lesson 5.3 Elastic Collisions
Apply the Conservation Laws for Momentum and Kinetic Energy to elastic collisions’ velocity:
- Know the masses and velocities before
- Determine velocity after collision:
vA + v’A = vB + v’B
Therefore: The relative speed after the collision has the same magnitude of the relative speed before the collision (regardless of mass)
vA - vB = v’B - v’A
Lesson 5.3 Elastic Collisions
25. (II) A ball of mass 0.440 kg moving east (+x direction) with a speed of 3.80 m/s collides head-on with a 0.220-kg ball at rest. If the collision is perfectly elastic, what will be the speed and direction of each ball after the collision?

Lesson 5.3 Elastic Collisions
27. (II) A 0.060-kg tennis ball, moving with a speed of 5.50 m/s, has a head-on collision with a 0.090- kg ball initially moving in the same direction at a speed of 3.00 m/s. Assuming a perfectly elastic collision, determine the speed and direction of each ball after the collision.

Lesson 5.3 Elastic Collisions
29. (II) A 0.280-kg croquet ball makes an elastic head-on collision with a second ball initially at rest. The second ball moves off with half the original speed of the first ball. (a) What is the mass of the second ball? (b) What fraction of the original kinetic energy (KE/KE) gets transferred to the second ball?

Lesson 5.4 Inelastic Collisions
What is an inelastic collision in relation to energy?
🔬 Inelastic Collisions are collisions in which kinetic energy is not conserved
- Some of the initial kinetic energy is transformed into another type of energy (thermal or potential energy)
- The inverse can also happen - potential energy (such as chemical or nuclear) is released, which causes the total kinetic energy after the interaction to be greater than the initial kinetic energy
- Ex: explosions
- Macroscopic collisions are inelastic to some extent
mv=(m+M)v’
Lesson 5.4 Inelastic Collisions
What is the final velocity formula for inelastic collisions?
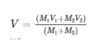
Lesson 5.4 Inelastic Collisions
What happens when a collision is completely inelastic?
Completely Inelastic: when two objects stick to each other
- The kinetic energy in some cases is all transformed to other forms of energy (or only part of it)
- The total energy is still conserved
Lesson 5.4 Inelastic Collisions
33. (I) In a ballistic pendulum experiment, projectile 1 result in a maximum height h of the pendulum equal to 2.6 cm. A second projectile (of the same mass) causes the pendulum to swing twice as high, h2 = 5.2 cm. The second projectile was how many times faster than the first?

Lesson 5.4 Inelastic Collisions
35. (II) A 28-g rifle bullet traveling 190 m/s embeds itself in a 3.1-kg pendulum hanging on a 2.8-m long string, which makes the pendulum swing upward in an arc. Determine the vertical and horizontal components of the pendulum’s maximum displacement.

Lesson 5.4 Inelastic Collisions
37. (II) A 980-kg sports car collides into the rear end of a 2300-kg SUV stopped at a red light. The bumpers lock, the brakes are locked, and the two cars skid forward 2.6 m before stopping. The police officer, estimating the coefficient of kinetic friction between tires and road to be 0.80, calculates the speed of the sports car at impact. What was that speed?

Lesson 5.5 Center of Mass (CM)
What is the General Motion of an Extended Object?
- Momentum used to analyze the motion of extended bodies (an object that has size)
- Assumed they approximate a point particle or undergoes translational motion
- Motion that is not a pure translation as general motion
🔬 General Motion of an Extended Object (or system of Objects): The sum of the translational motion of the CM, plus rotational, vibrational, or other types of motion around the CM
Lesson 5.5 Center of Mass (CM)
What is a centre of mass?
Center of Mass (CM): even if an object rotates, there is one point that moves in the same path that a particle would move is subjected to the same net force
- M = total mass of the system
- Center of mass lies on the line joining mA and mB
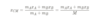
Lesson 5.5 Center of Mass (CM)
If one mass is greater than the other …
If one mass is greater than the other, then the CM is closer to the larger mass
Lesson 5.5 Center of Mass (CM)
If there are more than two particles along a line …
If there are more than two particles along a line, there will be additional terms

Lesson 5.5 Center of Mass (CM)
If the two masses are equal then xCM is …
If the two masses are equal then xCM is midway between them

Lesson 5.5 Center of Mass (CM)
How does the center of mass depend on the frame of reference?
- CM depends on the reference frame or coordinate system
- Physical location is dependent on the choice
- If the particle is spread over two or three dimensions, must specific the other (y and z) coordinates as well:

Lesson 5.5 Center of Mass (CM)
What is the center of gravity (CG)?
🔬 Center of Gravity (CG) is the point at which the force of gravity can be considered to act
- Force of gravity actually acts on all the different parts of an object
- For translational motion - assume the entire weight of the object acts as the CG
- For all practical purposes the center of mass = center of gravity
Lesson 5.5 Center of Mass (CM)
If an object is suspended from any point … (CG)
If an object is suspended from any point: swing a vertical line directly below the point
Lesson 5.5 Center of Mass (CM)
If the object is two dimensional/ has a plane of symmetry …
If the object is two dimensional/ has a plane of symmetry: only be bung from two different pivot points and respective vertical (plumb) lines drawn
Lesson 5.5 Center of Mass (CM)
If the object is symmetrically shaped …
If the object is symmetrically shaped: CM is located at the geometric center of the object
Lesson 5.5 Center of Mass (CM)
49. (I) The distance between a carbon atom (m = 12 u) and an oxygen atom (m = 16 u) in the CO molecule is 1.13 × 10–10 m. How far from the carbon atom is the center of mass of the molecule?
Lesson 5.5 Center of Mass (CM)
51. (II) The CM of an empty 1250-kg car is 2.40 m behind the front of the car. How far from the front of the car will the CM be when two people sit in the front seat 2.80 m from the front of the car, and three people sit in the back seat 3.90 m from the front? Assume that each person has a mass of 65.0 kg.

Lesson 5.5 Center of Mass (CM)
53. (II) A (lightweight) pallet has a load of ten identical cases of tomato paste (see Fig. 7–39), each of which is a cube of length l. Find the center of gravity in the horizontal plane, so that the crane operator can pick up the load without tipping it.

Quiz 5.3
The graph in the figure shows the x component F of the net force that acts for 10 s on a 100-kg crate. What is the change in the momentum of the crate during the 10 s that this force acts?
- 25 kg ∙ m/s
- 75 kg ∙ m/s
- -75 kg ∙ m/s
- -25 kg ∙ m/s
- -100 kg ∙ m/s

- -75 kg ∙ m/s
Quiz 5.3
Two ice skaters suddenly push off against one another starting from a stationary position. The 45-kg skater acquires a speed of 0.375 m/s relative to the ice. What speed does the 60-kg skater acquire relative to the ice?
- 0.75 m/s
- 0.00 m/s
- 0.50 m/s
- 0.38 m/s
- 0.28 m/s
- 0.28 m/s
Quiz 5.3
A batter hits a 0.140-kg baseball that was approaching him at 30 m/s and, as a result, the ball leaves the bat at 40 m/s in the reverse of its original direction. The ball remains in contact with the bat for 2.0 ms. What is the magnitude of the average force exerted by the bat on the ball?

Quiz 5.3
A 60-kg swimmer suddenly dives horizontally from a 150-kg raft with a speed of 1.5 m/s. The raft is initially at rest. What is the speed of the raft immediately after the diver jumps if the water has negligible effect on the raft?

Quiz 5.3
A 328-kg car moving at 19.1 m/s in the +x direction hits from behind a second car moving at in the same direction. If the second car has a mass of and a speed of right after the collision, what is the velocity of the first car after this sudden collision?
- 24.2 m/s
- 14.0 m/s
- 18.2 m/s
- -14.0 m/s
- 14.0 m/s
Quiz 5.3
A 475-gram ball is traveling horizontally at 12.0 m/s to the left when it is suddenly struck horizontally by a bat, causing it to reverse direction and initially travel at 8.50 m/s to the right. If the bat produced an average force of 1275 N on the ball, for how long (in milliseconds) was it in contact with the ball?

Quiz 5.3
Identical forces act for the same length of time on two different objects. The magnitude of the change in momentum of the lighter object is
- exactly equal to the magnitude of the change in momentum of the larger mass.
- smaller than the magnitude of the change in momentum of the larger mass, but not zero.
- There is not enough information to answer the question.
- larger than the magnitude of the change in momentum of the larger mass.
- zero.
- exactly equal to the magnitude of the change in momentum of the larger mass
Quiz 5.3
A tiger is running in a straight line. If we double both the mass and speed of the tiger, the magnitude of its momentum will increase by what factor?
- 16
- 4
- 8
- 2
- 4
Quiz 5.3
Two astronauts, of masses 60 kg and 80 kg, are initially right next to each other and at rest in outer space. They suddenly push each other apart. What is their separation after the heavier astronaut has moved 12 m?
- 16 m
- 24 m
- 9.0 m
- 21 m
- 28 m
- 28 m
Quiz 5.3
Two air track carts move along an air track towards each other. Cart A has a mass of 450 g and moves toward the right with a speed of 0.850 m/s. Cart B has a mass of 300 g and moves toward the left with a speed of 1.12 m/s. What is the total momentum of the two-cart system?
- 0.750 kg ∙ m/s toward the left
- 0.047 kg ∙ m/s toward the right
- 0.719 kg ∙ m/s toward the right
- 0.750 kg ∙ m/s toward the right
- 0.719 kg ∙ m/s toward the left
- 0.047 kg ∙ m/s toward the right
Quiz 5.3
A batter applies an average force of 8000 N to a baseball for 1.1 ms. What is the magnitude of the impulse delivered to the baseball by the bat?
p = 8.8 N * s

Quiz 5.3
What is the magnitude of the momentum of a 0.140 kg baseball traveling at 45.0 m/s?

Quiz 5.3
A 14,000-kg boxcar is coasting at 1.50 m/s along a horizontal track when it suddenly hits and couples with a stationary 10,000-kg boxcar. What is the speed of the cars just after the collision?

Quiz 5.3
An empty train car of mass 2.0 x 104 kg coasts along at 10 m/s. A 3000-kg boulder is suddenly dropped vertically into the car. Find the speed of the car immediately after the boulder is dropped in.

Quiz 5.3
A 0.10-kg ball, traveling horizontally at 25 m/s, strikes a wall and rebounds at 19 m/s. What is the magnitude of the change in the momentum of the ball during the rebound?
- 72 kg ∙ m/s
- 1.8 kg ∙ m/s
- 4.4 kg ∙ m/s
- 1.2 kg ∙ m/s
- 5.4 kg ∙ m/s
- 4.4 kg ∙ m/s
Quiz 5.3
Jennifer hits a stationary 0.20-kg ball, and it leaves her racket at 40 m/s. Time-lapse photography shows that the ball was in contact with the racket for 40 ms.
- *(a)** What average force did the ball exert on the racket?
- *(b)** What is the ratio of this force to the weight of the ball?
(a) 0.20 kN
(b) 100

Quiz 5.3
Find the magnitude and direction of the net momentum of the system shown in the figure. Express the direction by giving the angle the net momentum makes with the +x-axis.
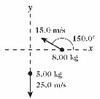

Quiz 5.3
A very light ping-pong ball moving east at a speed of 4 m/s collides with a very heavy stationary bowling ball. The Ping-Pong ball bounces back to the west, and the bowling ball moves very slowly to the east. Which object experiences the greater magnitude impulse during the collision?
- the Ping-Pong ball
- It is impossible to tell since the actual mass values are not given.
- the bowling ball
- It is impossible to tell since the velocities after the collision are unknown.
- Neither; both experienced the same magnitude impulse.
- Neither; both experienced the same magnitude impulse
Quiz 5.3
A 0.14-kg baseball is dropped from rest from a height of 2.0 m above the ground. What is the magnitude of its momentum just before it hits the ground if we neglect air resistance?
- 0.88 kg ∙ m/s
- 0.28 kg ∙ m/s
- 1.4 kg ∙ m/s
- 0.62 kg ∙ m/s
- 0.44 kg ∙ m/s
- 0.88 kg ∙ m/s
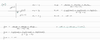
Since it is a freefalling object, it will only have a horizontal component and the acceleration will be equal to gravity. Therefore,
v^2 = -2g(y2-y1)
v = 6.26 m/s
Hence,
p = (0.14 kg)(6.26 m/s) = 0.88 kg * m/s (Option A)
Quiz 5.3
A 0.17-kg baseball is thrown with a speed of 38 m/s and it is hit straight back toward the pitcher with a speed of 62 m/s. What is the magnitude of the impulse exerted upon the ball by the bat?
p = 17 N*s

Module 5 Exam
(1) The momentum of an isolated system is conserved
- only in inelastic collisions.
- only in elastic collisions.
- in both elastic and inelastic collisions.
- in both elastic and inelastic collisions.
Module 5 Exam
You are standing on a skateboard, initially at rest. A friend throws a very heavy ball towards you. You have two choices about what to do with the ball: either catch the ball or deflect it back toward your friend with the same speed as it was originally thrown. Which choice should you make in order to maximize your speed on the skateboard?
- Catch the ball.
- Your final speed on the skateboard will be the same regardless whether you catch the ball or deflect the ball.
- Deflect the ball back.
- Deflect the ball back
Module 5 Exam
Consider two less-than-desirable options. In the first you are driving 30 mph and crash head-on into an identical car also going 30 mph. In the second option you are driving 30 mph and crash head-on into a stationary brick wall. In neither case does your car bounce back from the thing it hits, and the collision time is the same in both cases. Which of these two situations would result in the greater impact force on your car?
- hitting the other car
- The force would be the same in both cases.
- hitting the brick wall
- None of the above choices are correct.
- The force would be the same in both cases
Module 5 Exam
A rocket explodes into two fragments, one 25 times heavier than the other. The magnitude of the momentum change of the lighter fragment is
- 1/25 as great as the momentum change of the heavier fragment.
- 5 times as great as the momentum change of the heavier fragment.
- 25 times as great as the momentum change of the heavier fragment.
- The same as the momentum change of the heavier fragment.
- 1/4 as great as the momentum change of the heavier fragment.
- The same as the momentum change of the heavier fragment
Module 5 Exam
In a collision between two unequal masses, which mass receives a greater magnitude impulse?
- They receive equal impulses.
- the smaller mass
- the larger mass
- They receive equal impulses
Module 5 Exam
A railroad car collides with and sticks to an identical railroad car that is initially at rest. After the collision, the kinetic energy of the system
- is one third as much as before.
- is half as much as before.
- is one quarter as much as before.
- is the same as before.
- is one fourth as much as before.
- is half as much as before
Module 5 Exam
A firecracker explodes in midair and breaks up into many fragments. Which of the following statements are true regarding conditions immediately before and immediately after the explosion:
I. The total momentum of the fragments is equal to the original momentum of the firecracker.
II. The total kinetic energy of the fragments is equal to the original kinetic energy of the firecracker.
- Statement II only
- Neither statement is true.
- Both Statement I and Statement II
- Statement I only
- Statement I only
Module 5 Exam
There must be equal amounts of mass on both sides of the center of mass (or center of gravity) of a system.
True or False
False
Module 5 Exam
Two air track carts move along an air track towards each other. Cart A has a mass of 450 g and moves toward the right with a speed of 0.850 m/s. Cart B has a mass of 300 g and moves toward the left with a speed of 1.12 m/s. What is the total momentum of the two-cart system?
- 0.719 kg ∙ m/s toward the left
- 0.719 kg ∙ m/s toward the right
- 0.750 kg ∙ m/s toward the right
- 0.047 kg ∙ m/s toward the right
- 0.750 kg ∙ m/s toward the left
- 0.047 kg ∙ m/s toward the right
Module 5 Exam
A firecracker breaks up into two pieces, one of which has a mass of 200 g and flies off along the +x-axis with a speed of 82.0 m/s. The second piece has a mass of 300 g and flies off along the +y-axis with a speed of 45.0 m/s. What is the total momentum of the two pieces?
- 361 kg ∙ m/s at 56.3° from the +x-axis
- 21.2 kg ∙ m/s at 56.3° from the +x-axis
- 21.2 kg ∙ m/s at 39.5° from the +x-axis
- 93.5 kg ∙ m/s at 28.8° from the +x-axis
- 361 kg ∙ m/s at 0.983° from the +x-axis
3. 21.2 kg ∙ m/s at 39.5° from the +x-axis
Determine x and y components and use the Pythagorean theorem and tan Θ to determine the final momentum and direction.
Module 5 Exam
A 600-kg car makes a 90° turn. Its speed before the turn is 21.0 m/s and after the turn it is 24.0 m/s. What is the magnitude of the change in the car’s momentum during the turn?
- 12.0 × 103 kg∙m/s
- 19.1 × 103 kg∙m/s
- 10.2 × 103 kg∙m/s
- 9.55 × 103 kg∙m/s
- 22.2 × 103 kg∙m/s
2. 19.1 × 103 kg∙m/s
Break into x- and y-components and find vinal velocity via the Pythagorean Theorem and them multiply with the mass of the car.
Module 5 Exam
A 60-kg swimmer suddenly dives horizontally from a 150-kg raft with a speed of 1.5 m/s. The raft is initially at rest. What is the speed of the raft immediately after the diver jumps if the water has negligible effect on the raft?
The speed of the raft after the diver jumped is 0.6 m/s in the opposite direction of the diver.

Module 5 Exam
A 14,000-kg boxcar is coasting at 1.50 m/s along a horizontal track when it suddenly hits and couples with a stationary 10,000-kg boxcar. What is the speed of the cars just after the collision?

Module 5 Exam
A 1200-kg cannon suddenly fires a 100kg cannonball at 35 m/s. What is the recoil speed of the cannon? Assume that frictional forces are negligible and the cannon is fired horizontally.
- 2.9 m/s
- 35 m/s
- 3.5 m/s
- 3.2 m/s
- 2.9 m/s
Module 5 Exam
Two astronauts, of masses 60 kg and 80 kg, are initially right next to each other and at rest in outer space. They suddenly push each other apart. What is their separation after the heavier astronaut has moved 12 m?
- 21 m
- 16 m
- 9.0 m
- 28 m
- 24 m
- 28 m
v1’ = m2v2/m1 = -1.33v2’
x1 = v1‘t
x2 = v2‘t
x1 = (-1.33v2‘)t * 12/v2’ = -16 m
Total Displacement = 16 m + 12 m = 28m
Module 5 Exam
A batter hits a 0.140-kg baseball that was approaching him at 30 m/s and, as a result, the ball leaves the bat at 40 m/s in the reverse of its original direction. The ball remains in contact with the bat for 2.0 ms. What is the magnitude of the average force exerted by the bat on the ball?

Module 5 Exam
A 0.17-kg baseball is thrown with a speed of 38 m/s and it is hit straight back toward the pitcher with a speed of 62 m/s. What is the magnitude of the impulse exerted upon the ball by the bat?

Module 5 Exam
Calculate the impulse due to a force of 4.5N that lasts for 1.4s
- 6.9 kg∙ m/s
- 5.0 kg∙ m/s
- 6.3 kg∙ m/s
- 6.3 kg∙ m/s
Module 5 Exam
A force of 5.3 N is needed to hold on to an umbrella in a strong wind. If the air molecules each have a mass of 4.7 ×10-26 kg, and each one strikes the umbrella (without rebounding) with a speed of 2.0 m/s in the same direction, how many atoms strike the umbrella each second? Assume that the wind blows horizontally so that the gravity can be neglected.
Module 5 Exam
A 2.0-kg mass moving at 5.0 m/s suddenly collides head-on with a 3.0-kg mass at rest. If the collision is perfectly inelastic, what is the speed of the masses just after the collision?
- 2.5 m/s
- 10 m/s
- 0 m/s, since the collision is inelastic
- 2.0 m/s
- 2.0 m/s
Module 5 Exam
A 50-g ball moving at 10 m/s in the +x direction suddenly collides head-on with a stationary ball of mass 100 g. If the collision is perfectly elastic, what is the velocity of each ball immediately after the collision?
- -3.3 m/s, +6.7 m/s
- +3.3 m/s, -6.7 m/s
- +6.7 m/s, -3.3 m/s
- -6.7 m/s, +3.3 m/s
- -3.3 m/s, +6.7 m/s
Module 5 Exam
An 80-kg man is skating northward and happens to suddenly collide with a 20-kg boy who is ice skating toward the east. Immediately after the collision, the man and boy are seen to be moving together at 2.5 m/s in a direction 60° north of east. How fast was the boy moving just before the collision?

Module 5 Exam
A car heading north suddenly collides at an intersection with a truck of the same mass heading east. If they lock together and travel at 28 m/s at 15° north of east just after the collision, how fast was the car initially traveling?
- 14 m/s
- 28 m/s
- 7 m/s
- 11 m/s
- 14 m/s
Module 5 Exam
A 0.32-kg ball is moving horizontally at 30 m/s just before suddenly bouncing off a wall Just after the bounce, it is moving horizontally at 25 m/s but in the opposite direction.
- *(a)** What is the magnitude of the change in momentum of the ball during the bounce?
- *(b)** What percentage of the ball’s original kinetic energy was lost in the collision?
(a) 18 N ∙ s
(b) 31%

Module 5 Exam
A block of mass m = 9.0 kg and speed V and is behind a block of mass M = 27 kg and speed of as shown int the figure. The surface is frictionless, and the blocks suddenly collide and couple. After the collision, the blocks have a common speed of 0.90 m/s. How much kinetic energy of the blocks is lost due to the collision?
- 11 J
- 8.6 J
- 2.0 J
- 31 J
- 4.6 J
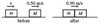
- 8.6 J
Module 5 Exam
An 8.0-g bullet is suddenly shot into a 4.0-kg block that is at rest on a frictionless horizontal surface, as shown in the figure. The bullet remains lodged in the block. The block then moves against a spring and compresses it by 3.7 cm. The force constant (spring constant) of the spring is 2500 N/m.
What was the initial speed v of the bullet?
- 440 m/s
- 460 m/s
- 480 m/s
- 500 m/s
- 520 m/s

- 460 m/s
Module 5 Exam
A baseball pitcher is employing a ballistic pendulum to determine the speed of his fastball. A 3.3 kg lump of clay is suspended from a cord 2.0 m long. When the pitcher throws his fastball aimed directly at the clay, the ball suddenly becomes embedded in the clay and the two swing up to a maximum height of 0.080 m. If the mass of the baseball is 0.21 kg, find the speed of the pitched ball.

Module 5 Exam
A 1200-kg pick-up truck traveling south at 15 m/s suddenly collides with a 750-kg car that is traveling east. The two vehicles stick together and slide along the road after colliding. A highway patrol officer investigating the accident determines that the final position of the wreckage after the collision is 25 m, at an angle of 50° south of east, from the point of impact. She also determines that the coefficient of kinetic friction between the tires and the road at that location was 0.40. What was the speed of the car just before the collision?
- 20 m/s
- 14 m/s
- 23 m/s
- 17 m/s
- 4.8 m/s
- 23 m/s
Module 5 Exam
Three small masses are positioned at the following coordinates: 3.0 kg at (3.0 m, 2.0 m); 4.0 kg at (0.0 m, -1.0 m); and 5.0 kg at (5.0 m, -7.0 m). What are the coordinates of the center of mass (or center of gravity) of this system?

Module 5 Exam
A 1.0-g bead is at (-2.0 cm, 2.0 cm), a 2.0-g bead is at (2.0 cm, -4.0 cm), and a 3.0-g bead is at (2.0 cm, 0.0 cm). What are the coordinates of the center of mass (or center of gravity) of this system of beads?