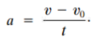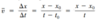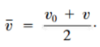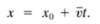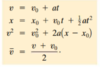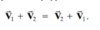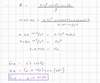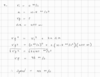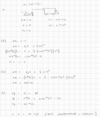Module 01: Kinematics Flashcards
Lesson 1.1 - Speed, Velocity, and Acceleration Lesson 1.2 - Motion at Constant Acceleration, Freely Falling Objects, and Graphical Analysis Lesson 1.3 - Vector Addition Lesson 1.4 - Projectile Motion
Lessson 1.1 - Speed and Velocity and Acceleration
Define Mechanics:
Mechanics is the study of the motion of objects, and the related concepts of force and energy.
Lessson 1.1 - Speed and Velocity and Acceleration
What are the two fields of mechanics?
- Kinematics (description of how objectives move)
- Dynamics (deals with the forces and why objects move as they do)
Lessson 1.1 - Speed and Velocity and Acceleration
What is translational motion?
Objects that move without rotating
Lessson 1.1 - Speed and Velocity and Acceleration
What is the idealized particle?
- mathematical point with no spatial size (no size)
- Can only go through translational motion
Lessson 1.1 - Speed and Velocity and Acceleration
What is a reference frame and why is it important?
Any measurement of position, distance, or speed needs a reference frame.
- Important to specify
- Need to say “with respect to Earth” to avoid confusion
Lessson 1.1 - Speed and Velocity and Acceleration
What are important aspects of the motion of an object?
(1) SPEED and (2) DIRECTION of motion
Lessson 1.1 - Speed and Velocity and Acceleration
Define distance and displacement
Distance: Change in position of the object
Displacement: How far the object is from its starting point
Lessson 1.1 - Speed and Velocity and Acceleration
What are the components of a vector? Does displacement qualify?
Vectors have both (1) MAGNITUDE and (2) DIRECTION (and displacement qualifies)
Lessson 1.1 - Speed and Velocity and Acceleration
What does the sign of movement along a line (vector in one dimension)?
Lessson 1.1 - Speed and Velocity and Acceleration
What is the formula for displacement?
Δx = x2 - x1
- Δx = Displacement
- x2 - x1 = Position Two minus Position One
Lessson 1.1 - Speed and Velocity and Acceleration
What does “speed” refer to?
How far an object travels in a given amount of time
Lessson 1.1 - Speed and Velocity and Acceleration
What is average speed?
Total distance traveled along its path is divided by the time it takes to travel the distance
Lessson 1.1 - Speed and Velocity and Acceleration
What is the difference between velocity and speed?
- Speed: positive number (with units)
- Velocity: signify both (1) magnitude and (2) direction [meaning its a vector]
- Furthermore, the average velocity is displacement over time (rather than distance)
Lessson 1.1 - Speed and Velocity and Acceleration
What is average velocity?
- Displacement divided by the elapsed time
Lessson 1.1 - Speed and Velocity and Acceleration
When does average speed and average velocity have the same magnitude?
If the motion of an object is along a straight line and in the same direction, the magnitude of displacement is equal to the total path length. In that case, the magnitude of the average velocity is equal to the average speed.
Lessson 1.1 - Speed and Velocity and Acceleration
Define instantaneous velocity (and the formula).
- The average velocity over an infinitesimally short time interval*
- Evaluated in the limit of Δt becomes extremely small (approaching zero)
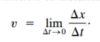
Lessson 1.1 - Speed and Velocity and Acceleration
Why is the instantaneous speed always equal to the magnitude of the displacement?
because the distance traveled and the magnitude of the displacement becomes the same when they are infinitesimally small
Lessson 1.1 - Speed and Velocity and Acceleration
When the average velocity and the velocity equal to each other?
When an object moves at a uniform velocity during a particular time
Lessson 1.1 - Speed and Velocity and Acceleration
What is acceleration?
Specifies how rapidly the velocity of an object is changing
SI units of acceleration: m/s2
Lessson 1.1 - Speed and Velocity and Acceleration
What is the average acceleration?
Velocity is divided by the time taken to make this change.
Lessson 1.1 - Speed and Velocity and Acceleration
What is instantaneous acceleration?
Analogy to instantaneous velocity as the average acceleration over an infinitesimally short time interval at a given time:
Lessson 1.1 - Speed and Velocity and Acceleration
What is deceleration?
- Object is slowing down
- Not mean that acceleration is necessarily negative
Lessson 1.1 - Speed and Velocity and Acceleration
What is the formula for displacement when the acceleration is constant?
Δx = vi Δt + 1/2 a (Δt)2
- Δx: displacement
- vi: initial velocity
- Δt: change in time
- a: acceleration (must be constant)
Lessson 1.1 - Speed and Velocity and Acceleration
What direction is acceleration when the velocity is negative?
Positive (acceleration is always the opposite direction than velocity)
Lesson 1.2 - Motion at Constant Acceleration, Freefalling Objects, and Graphical Analysis
When is motion in a strait line?
When acceleration is constant.
Lesson 1.2 - Motion at Constant Acceleration, Freefalling Objects, and Graphical Analysis
What happens at constant acceleration?
- Motion is in a straight line
- Instantaneous and average acceleration are equal
Lesson 1.2 - Motion at Constant Acceleration, Freefalling Objects, and Graphical Analysis
How does the notation change when discussing constant acceleration?
Initial time at zero: t0. Therefore, t1 = t0 = 0
Elaposed time: t2 = t
Initial position (x1 = x0) and Initial velocity (v1 = v0)
Hence,
Lesson 1.2 - Motion at Constant Acceleration, Freefalling Objects, and Graphical Analysis
What is the average velocity over the time interval t - t0:
Lesson 1.2 - Motion at Constant Acceleration, Freefalling Objects, and Graphical Analysis
Formula to solve for the velocity of an object after any time elapsed when we are given the object’s constant acceleration:
v = v0 + at
Lesson 1.2 - Motion at Constant Acceleration, Freefalling Objects, and Graphical Analysis
Formula to determine the average velocity using initial and final velocity: (assuming constant acceleration)
Lesson 1.2 - Motion at Constant Acceleration, Freefalling Objects, and Graphical Analysis
Formula to find the position of x after a time t when it undergoes constant acceleration:
Lesson 1.2 - Motion at Constant Acceleration, Freefalling Objects, and Graphical Analysis
What are the four Kinematic Equations for Constant Acceleration?
- Only valid when a = constant.
- Set x0=0 for simplicity
- x = position (not distance)
- Displacement: x-x0
Lesson 1.2 - Motion at Constant Acceleration, Freefalling Objects, and Graphical Analysis
What is the problem-solving strategy for physics?
- Read the question
- Decide what object you are going to study, and for what time interval. (ex. t = 0)
- Draw a diagram of the situation
- Write down the “knows” or “givens” and what you want to know
- Think about the principles of physics apply in the problem
- Consider which equations are related to the quantities involved.
- Carry out the calculations in its a numerical problem (Keep one or two extra digits in the calculations)
- Think about the result: IS IT REASONABLE?
- Always keep track of UNITS.
Lesson 1.2 - Motion at Constant Acceleration, Freefalling Objects, and Graphical Analysis
Describe the acceleration of a freefalling object:
Example of UNIFORM ACCELERATION
- Used to believe that heavier objects fall faster than lighter objects and that speed is proportional to how heavy an object is
- Truth: The Speed of a falling object is not proportional to its mass!
- Galileo’s contribution to the understanding of motion of falling objects:
- At a given location on the Earth and in the absence of air resistance, all objects fall with the same constant acceleration*
Lesson 1.2 - Motion at Constant Acceleration, Freefalling Objects, and Graphical Analysis
Why is Galileo the “father of modern mathematics?”
Not for the content of his science by for his new methods of doing science ((idealization and simplification, mathematization of theory)
Ex. Realized that freefalling objects have a uniform acceleration
Lesson 1.2 - Motion at Constant Acceleration, Freefalling Objects, and Graphical Analysis
What is the acceleration due to gravity?
At a given location on the Earth and in the absence of air resistance, all objects fall with the same constant acceleration - Galileo
Magnitude: g = 9.80m/s2
(1) Vector and (2) Direction is downwards towards earth
Lesson 1.2 - Motion at Constant Acceleration, Freefalling Objects, and Graphical Analysis
How do equations change when dealing with free-falling objects?
- a = g = 9.80m/s2
- y0 takes the place of x0 (since the motion is vertical)
Lesson 1.2 - Motion at Constant Acceleration, Freefalling Objects, and Graphical Analysis
Why is the trowing action not part of acceleration?
During the throw, the hand is touching the ball and the acceleration is unknown to us. Only consider when the ball is in the air and the acceleration is equal to g .
Lesson 1.2 - Motion at Constant Acceleration, Freefalling Objects, and Graphical Analysis
How is acceleration of rockets and fast airplanes measured?
Multiples of g.
Ex. a Plane pulling out of a dive and undergoing 3 g’s has an acceleration of (3.00)(9.80m/s2)
Lesson 1.2 - Motion at Constant Acceleration, Freefalling Objects, and Graphical Analysis
What is the average velocity of an object (based on a graph)?
The Average Velocity of an object during any time interval ▲t = t2 - t1 is equal to the slope of the straight line (or chord) connecting the two points.
Lesson 1.2 - Motion at Constant Acceleration, Freefalling Objects, and Graphical Analysis
What is the instantaneous velocity (from a graph)?
The Instantaneous Velocity equals the slope of the tangent to the curve of x vs. t at any chosen point.
What is the velocity-time graph for an object thrown (1) upwards, (2) downwards, and (3) released from rest?
- Object thrown downwards: linear graph with a negative intercept and a negative slope
- Object thrown upwards: linear velocity-time graph with a positive intercept and a negative slope
- Object released from rest: linear slope with an intercept at zero and a negative slope
Lesson 1.3 - Vector Addition
What is a vector quantity?
Direction as well as the magnitude
Lesson 1.3 - Vector Addition
What is a scalar quantity?
Quantities have no direction associated with them
(mass, time, and temperature)
Lesson 1.3 - Vector Addition
How can scalar quantities be added?
- Added using arithmetic (also be used for vectors if they have the same direction)
- Total = called the net or resultant displacement
Lesson 1.3 - Vector Addition
What is the method to determining the resultant displacement (when directional quantities are perpendicular)?
- Use the pythagorean theorem
Lesson 1.3 - Vector Addition
What is the vector equation?
Adding two vectors: the magnitude of the resultant vector is not equal to the sum of the magnitudes of the two separate vectors
Rules:
- Draw one vector D1 to scale
- Draw D2 to scale, placing the tail at the tip of the second vector
- The arrow drawn from the tail of the first vector to the tip of the second vector represents the sum (or resultant) of the two vectors
Lesson 1.3 - Vector Addition
What is the tail-to-tip method for adding vectors?
Note that vectors can be moved parallel to themselves on paper
- Draw one vector D1 to scale
- Draw D2 to scale, placing the tail at the tip of the second vector
- The arrow drawn from the tail of the first vector to the tip of the second vector represents the sum (or resultant) of the two vectors
Lesson 1.3 - Vector Addition
What is the parallelogram method to add vectors?
- Vectors drawn from a common origin and a parallelogram is constructed using two vectors as adjacent sides
- A diagonal drawn from the common origin
Lesson 1.3 - Vector Addition
What is a negative vector?
(1) Same magnitude but (2) opposite direction
- V
Lesson 1.3 - Vector Addition
How do you add two vectors?
The difference between two vectors:
Lesson 1.3 - Vector Addition
How can you multiply two vectors?
Vector can be multiplied by a scalar (c)
Product: cV
- Same direction as V and the magnitude of cV
Lesson 1.3 - Vector Addition
What are components?
V: sum of two vectors which are the components of the original vector
Process of finding the components: resolving the vector into its components
- Vector components: both magnitude and direction
- Scalar components: just magnitude
Lesson 1.3 - Vector Addition
How do you add vectors?
- Resolve each vector into its components
- Hence, VRY = V1Y + V2Y (not add x and y components together)
The sum of two vectors of fixed magnitudes has the greatest magnitude when the angle between these two vectors is:
0°
Lesson 1.4 - Projectile Motion
What is projectile motion?
Ex: golf ball, the Earth’s surface, and batted baseball
Action that is taking place in two dimensions if there is no wind
Lesson 1.4 - Projectile Motion
What is air resistance’s role in projectile motion?
- Often important (many cases its effect can be ignored)
- Ignore it in the following analysis
We consider only its motion after it has been projected, and before it lands or is caught - only analyse when it is moving freely through the air under the action of gravity alone.
Acceleration of the object due to gravity: g = 9.80 m/s2
Lesson 1.4 - Projectile Motion
How will the time between an object dropped vertically and horizontally differ?
An object projected horizontally will reach the ground in the same time as an object dropped vertically
Vertical motion in both cases are the same
Lesson 1.4 - Projectile Motion
What is the formula for the vertical and horizontal components of a ball dropped from a table?
y = y0 + vy0 + 1/2 ayt2
x = vx0t + 1/2 axt2 = vx0t
Lesson 1.4 - Projectile Motion
What are the General Kinematic Equations for Constant Acceleration in Two Dimensions
Lesson 1.4 - Projectile Motion
What are the Kinematic Equations for Projectile Motion?
Lesson 1.4 - Projectile Motion
If projection angle Θ0 is chosen relative to the +x axis then:
Lesson 1.4 - Projectile Motion
What are the steps to solving Projectile Motion Questions?
1. Read carefully
- Draw a careful diagram showing what is happening
- Choose an origin and an xy coordinate system
- Decide on a time interval
- Examine the horizontal (x) and vertical (y) motions separately. If you are given the initial velocity, you may want to resolve it into x and y components
- List the known and unknown quantities:
ax = 0
ay = -g or +g
(Remember that vx never changes throughout the trajectory and vy = 0 at the highest point of any trajectory that returns downwards - Apply the relevant equations
What is the level horizontal range equations?
What is kinematics?
a study of how things move, without regard to the cause
What is the difference between position and displacement?
Position:
- Location in space
- Scalar quantity
Displacement:
- Change in position
- Vector quantity
What is the velocity (instantaneous and average)?
🔬 Velocity: Rate of change of an object’s displacement
- Average Velocity:
displacement/time
va =(v0+v1)/2
-
Instantaneous Velocity:
v = dx/dy - Displacement related to the (constant) velocity:
x=x0+vt
What are particle models and motion diagrams?
Particle model: single point on the page
Motion diagram: position of an object at equally-spaced time intervals
- Unequal spacing between successive points indicate that velocity is changing
- Equal spacing between points indicate time
What is a net arrow?
Net Arrow: difference in length between two successive arrows on a motion diagram indicates the relative magnitude and direction of the change in velocity
How does the direction of acceleration and velocity relate?
- Acceleration points same direction as the velocity vector: velocity increases
- Acceleration points in the opposite direction as the velocity: velocity decreases
What is instantaneous acceleration?
Found by reducing the time elapsed to a very small value
- Derivative for velocity: a = dv/dt
- Second derivative for dispalcement: ax=d2x/dt2
What are the kinematic equations?
where x is the final position, x0 is the initial position, v is the final velocity, v0 is the initial velocity, a is acceleration, and t is the elapsed time.
What is a free-falling object’s acceleration?
Constant accelerating equal to the acceleration due to gravity
Describe the motion and acceleration of a ball moving up and down a ramp:
Linear acceleration of an object on a ramp = component of the acceleration due to gravity that points parallel to the slope of the incline:
a=g sinθ
Ball given an initial push and rolled up a ramp slows down, stops momentarily at the turning point, then starts to speed up and roll back down
Turning point: location where the velocity of a moving object with constant acceleration is momentarily zero
- Before the turning point is reached, the velocity and acceleration point in opposite directions like when a ball is tossed into the air and starts slowing down.
- After the turning point, the velocity and acceleration point in the same direction, like when the ball tossed into the air falls back toward the ground.
What is projectile motion?
🔬 Projectile Motion: motion of an object under the influence of gravity alone
- Two-dimensional motion requires the kinematic equations separated in each dimension:
- Includes free-falling objects in one dimension and those following parabolic motion
What are free-falling objects? How do they compare to objects in a parabolic path?
Free-Falling Objects:
- no horizontal velocity or acceleration
- moves only in the vertical direction under the influence of gravity
- Angle of lauch determines whether an object is free-falling or parabolic
Parabolic Path: has some initial velocity in the horizontal direction
What is a trajectory?
path of an object in the (x,y) plane - straight, vertical line or a parabola
How does horizontal and vertical motion compare?
Horizontal and vertical motion are independent
Factor connecting horizontal and vertical components: Time
Horizontal Motion:
- Horizontal direction has no acceleration
- Horizontal velocity remains constant
- Velocity has the same magnitude at each vertical position
Vertical Motion:
- Vertical direction has acceleration due to gravity
- Vertical velocity changes continuously (due to acceleration due to gravity)
- Two times will be calculated when the object travels:
Objects travel upwards with specified velocity in the positive direction
Object travels downwards with the same magnitude velocity in the negative direction
What is the range?
- Change in the initial angle or intial velocity of a projectile changes the range and the maximum height
- When air resistance is ignored, the mass and shape of the projectile do not affect the trajectory, range, or maximum height of the projectile
Lesson 1.1 Questions
1. (I) If you are driving 95 km/h along a straight road and you look to the side for 2.0s, how far do you travel during this inattentive period?
Lesson 1.1 Questions
3. (I) A particle at t1 = –2.0 s is at x1 = 4.8 cm and at t2 = 4.5 s is at x2 = 8.5 cm. What is its average velocity over this time interval? Can you calculate its average speed from these data? Why or why not?
Lesson 1.1 Questions
7. (II) You are driving home from school steadily at 95 km/h for 180 km. It then begins to rain and you slow to 65 km/h. You arrive home after driving 4.5 h. (a) How far is your hometown from school? (b) What was your average speed?
Lesson 1.1 Questions
11. (II) A car traveling 95 km/h is 210 m behind a truck traveling 75 km/h. How long will it take the car to reach the truck?
210 m = 0.21 km
F(x) = truck’s distance & G(x) = car’s distance
F(x) = 75x + 0.21 (where x is hours and F(x) is km)
G(x) = 95x (where x is hours and G(x) is km)
Determine where the car’s distance is equal to truck’s distance, so F(x) = G(x):
F(x) = G(x)
75x + 0.21 = 95x
0.0105 = x
Therefore, the car needs approximately 0.0105 hours or 38 seconds to reach the truck.
Lesson 1.1 Questions
13. (II) Two locomotives approach each other on parallel tracks. Each has a speed of 155 km/h with respect to the ground. If they are initially 8.5 km apart, how long will it be before they reach each other? (See Fig. 2–35.)
Lesson 1.1 Questions
19. (II) A sports car moving at constant velocity travels 120 m in 5.0 s. If it then brakes and comes to a stop in 4.0 s, what is the magnitude of its acceleration (assumed constant) in m/s2, and in g’s (g = 9.80 m/s2)?
Lesson 1.2 Questions
23. (I) A car accelerates from 14 m/s to 21 m/s in 6.0 s. What was its acceleration? How far did it travel in this time? Assume constant acceleration.
Lesson 1.2 Questions
25. (II) A baseball pitcher throws a baseball with a speed of 43 m/s. Estimate the average acceleration of the ball during the throwing motion. In throwing the baseball, the pitcher accelerates it through a displacement of about 3.5 m, from behind the body to the point where it is released (Fig. 2–37).
Therefore, the acceleration of the ball during the throwing motion is 264 m/s2.
Lesson 1.2 Questions
29. (II) A car traveling at 95 km/h strikes a tree. The front end of the car compresses and the driver comes to rest after traveling 0.80 m. What was the magnitude of the average acceleration of the driver during the collision? Express the answer in terms of “g’s,” where 1.00 g = 9.80 m/s2.
Therefore, the magnitude of the average acceleration is equal to 44 g’s.
Lesson 1.2 Questions
* 31. (II) Determine the stopping distances for an automobile going a constant initial speed of 95 km/h and human reaction time of 0.40 s: (a) for an acceleration a = –3.0 m/s2; (b) for a = –6.0 m/s2.
Therefore, the stopping distance is (a) 127 m and (b) 69 m.
Lesson 1.2 Questions
33. (II) A 75-m-long train begins uniform acceleration from rest. The front of the train has a speed of 18 m/s when it passes a railway worker who is standing 180 m from where the front of the train started. What will be the speed of the last car as it passes the worker? (See Fig. 2–38.)
Therefore, the speed of the final cart as it passes the worker is 21 m/s.
Lesson 1.2 Questions
35. (II) A runner hopes to complete the 10,000-m run in less than 30.0 min. After running at constant speed for exactly 27.0 min, there are still 1200 m to go. The runner must then accelerate at 0.20 m/s2 for how many seconds in order to achieve the desired time?
Therefore, the runner needs to accelerate for approximately 6.3 seconds to end in less than 30.0 minutes.
Lesson 1.2 Questions
39. (I) A stone is dropped from the top of a cliff. It is seen to hit the ground below after 3.55 s. How high is the cliff?
Therefore, the cliff is 61.8 m high.
Lesson 1.2 Questions
41. (II) A ball player catches a ball 3.4 s after throwing it vertically upward. With what speed did he throw it, and what height did it reach?
Therefore, the speed he threw it with is 17 m/s and it reached a height of 14 m.
Lesson 1.3 Questions
1. (I) A car is driven 225 km west and then 98 km southwest (45°). What is the displacement of the car from the point of origin (magnitude and direction)? Draw a diagram.
tan Θ = 69.3/302
Θ = 13°
Lesson 1.3 Questions
5. (II) V is a vector 24.8 units in magnitude and points at an angle of 23.4° above the negative x axis. (a) Sketch this vector. (b) Calculate Vx and Vy. (c) Use Vx and Vy to obtain (again) the magnitude and direction of V. [Note: Part (c) is a good way to check if you’ve resolved your vector correctly.]
Lesson 1.3 Questions
7. (II) Figure 3–33 shows two vectors, A and B, whose magnitudes are A = 6.8 units and B = 5.5 units. Determine C if (a) C = A +B (b) C = A – B, (c) C = B – A. Give the magnitude and direction for each.
Lesson 1.3 Questions
15. (II) The summit of a mountain, 2450 m above base camp, is measured on a map to be 4580 m horizontally from the camp in a direction 38.4° west of north. What are the components of the displacement vector from camp to summit? What is its magnitude? Choose the x axis east, y axis north, and z axis up.
Lesson 1.4 Questions
17. (I) A tiger leaps horizontally from a 7.5-m-high rock with a speed of 3.0 m/s. How far from the base of the rock will she land?
Lesson 1.4 Questions
19. (Edited) (II) Estimate by what factor a person can jump farther on the Moon as compared to the Earth if the takeoff speed and angle are the same. The acceleration due to gravity on the Moon is one-sixth what it is on Earth.
Lesson 1.4 Questions
25. (Edited) (II) A grasshopper hops along a level road. On each hop, the grasshopper launches itself at angle q0 = 45° and achieves a range R = 0.80 m. What is the average horizontal speed of the grasshopper as it hops along the road? Assume that the time spent on the ground between hops is negligible.
Lesson 1.4 Questions
31. (II) A rescue plane wants to drop supplies to isolated mountain climbers on a rocky ridge 235 m below. If the plane is traveling horizontally with a speed of 250 km/h (69.4 m/s), how far in advance of the recipients (horizontal distance) must the goods be dropped (Fig. 3–38)?
Module 01 Exams
If, in a parallel universe, π has the value 3.14149, express π in that universe to four significant figures.
- 3.1415
- 3.141
- 3.142
- 3.1414
- 3.141
Module 01 Exams
Add 3685 g and 66.8 kg and express your answer in milligrams (mg).
- 7.05 × 105 mg
- 7.05 × 104 mg
- 7.05 × 107 mg
- 7.05 × 106 mg
- 7.05 × 107 mg
Module 01 Exams
The length and width of a rectangle are 1.125 m and 0.606 m, respectively. Multiplying, your calculator gives the product as 0.68175. Rounding properly to the correct number of significant figures, the area should be written as
- 0.6818 m2.
- 0.68 m2.
- 0.682 m2.
- 0.68175 m2.
- 0.7 m2.
- 0.682 m2.
Module 01 Exams
How many nanoseconds does it take for a computer to perform one calculation if it performs 6.7 * 107 calculations per second?
- 65 ns
- 15 ns
- 11 ns
- 67 ns
2. 15 ns
Here’s how I would do it find the time taken in seconds to perform 1 task with the computer working at 6.7 x 107 tasks per second
So divide your 1 second by 6.7 x 107 = 14.925 x 10-9 seconds
Now find your time in nano seconds
Divide the time taken in seconds by the amount of seconds in a nano second, so 14.925 x 10-9 / 1 x 10-9
Gives you 14.925 nano seconds.
Module 01 Exams
Albert uses as his unit of length (for walking to visit his neighbors or plowing his fields) the albert (A), the distance Albert can throw a small rock. One albert is How many square alberts is equal to one acre? (1 acre = 43,560 ft2 = 4050 m2) 1.
Module 01 Exams
When is the average velocity of an object equal to the instantaneous velocity?
- only when the velocity is increasing at a constant rate
- never
- always
- when the velocity is constant
- only when the velocity is decreasing at a constant rate
- when the velocity is constant
Module 01 Exams
You drive 6.0 km at 50 km/h and then another 6.0 km at 90 km/h. Your average speed over the 12 km drive will be
- less than 70 km/h.
- equal to 70 km/h.
- greater than 70 km/h.
- It cannot be determined from the information given because we must also know directions traveled.
- exactly 38 km/h.
- less than 70 km/h
Module 01 Exams
Suppose that a car traveling to the west begins to slow down as it approaches a traffic light. Which of the following statements about its acceleration is correct?
- The acceleration is zero.
- Since the car is slowing down, its acceleration must be negative.
- The acceleration is toward the east.
- The acceleration is toward the west.
- The acceleration is toward the east
Module 01 Exams
A ball is thrown straight up, reaches a maximum height, then falls to its initial height. Which of the following statements about the direction of the velocity and acceleration of the ball as it is going up is correct?
- Both its velocity and its acceleration points downward.
- Both its velocity and its acceleration point upward.
- Its velocity points upward and its acceleration points downward.
- Its velocity points downward and its acceleration points upward.
- Its velocity points upward and its acceleration points downward
Module 01 Exams
Two objects are dropped from a bridge, an interval of 1.0 s apart. Air resistance is negligible. During the time that both objects continue to fall, their separation
- decreases.
- increases.
- decreases at first, but then stays constant.
- stays constant.
- increases at first, but then stays constant.
- increases
Module 01 Exams
A child standing on a bridge throws a rock straight down. The rock leaves the child’s hand at time t = 0 s. If we take upward as the positive direction, which of the graphs shown below best represents the acceleration of the stone as a function of time?
B.
Module 01 Exams
A race car circles 10 times around a circular 8.0-km track in 20 min. Using SI units
(a) what is its average speed for the ten laps?
(b) what is its average velocity for the ten laps?
(b) The average velocity is equal to zero since the displacement is zero (because the tract is circular so the starting and ending points are the same).
Module 01 Exams
Arthur and Betty start walking toward each other when they are 100 m apart. Arthur has a speed of 3.0 m/s and Betty has a speed of 2.0 m/s. How long does it take for them to meet? 1.
Module 01 Exams
The position x(t) of a particle as a function of time t is given by the equation x(t) = (3.5 m/s)t - (5.0 m/s2)t2. What is the average velocity of the particle between t = 0.30 s and t = 0.40 s? 1.
Module 01 Exams
A package is dropped from a helicopter that is moving upward at 15m/s. If it takes 8s before the package strikes the ground, how high above the ground was the package when it was released? Neglect air resistance. 1.
Module 01 Exams
At the same moment, one rock is dropped and one is thrown downward with an initial velocity of 29m/s from the top of a building that is 300m tall. How much earlier does the thrown rock strike the ground? Neglect air resistance. 1.
Module 01 Exams
A player kicks a soccer ball in a high arc toward the opponent’s goal. At the highest point in its trajectory
- the ball’s acceleration points upward.
- both the velocity and the acceleration of the soccer ball are zero.
- neither the ball’s velocity nor its acceleration are zero.
- the ball’s acceleration is zero but its velocity is not zero.
- the ball’s velocity points downward.
At the height of the projectile’s path, gravity is still an active force on the ball, so there is still acceleration. Furthermore, the Vy component is zero, since the parabola is at its maximum point and changing direction; however, the Vx component is still moving forwards as the ball is thrown. Therefore, the correct answer is (C) that neither the acceleration or velocity is equal to zero.
Module 01 Exams
A player throws a football 50.0 m at 61.0° north of west. What is the westward component of the displacement of the football?
- 0.00 m
- 24.2 m
- 64.7m
- 55.0 m
- 74.0 m
- 24.2 m
Module 01 Exams
The figure shows three vectors, A, B, and C, along with their magnitudes. Determine the magnitude and direction of the vector given by A - B - C.
Quiz 1.1
Under what condition is average velocity equal to the average of the object’s initial and final velocity?
- This can occur only when the velocity is zero.
- This can only occur if there is no acceleration.
- The acceleration must be constantly increasing.
- The acceleration is constant.
- The acceleration must be constantly decreasing.
- This can only occur if there is no acceleration
Quiz 1.1
If, in the figure, you start from the Bakery, travel to the Cafe, and then to the Art Gallery in 2.00 hours, what is your
average speed?
average velocity?
a. Average Speed: (Distance traveled ÷ time elapsed) = 10.5km/2.00hours=5.25kmh
b. Average Velocity: (Displacement ÷ time elapsed) = x2-x1/t2-t1=2.50km-0/km2.00hours=1.25kmh
Quiz 1.1
Suppose that a car traveling to the west (-x direction) begins to slow down as it approaches a traffic light. Which statement concerning its acceleration must be correct?
- Its acceleration is decreasing in magnitude as the car slows down.
- Its acceleration is negative.
- Its acceleration is positive.
- Its acceleration is zero.
- Its acceleration is positive.
Quiz 1.1
A racing car accelerates uniformly from rest along a straight track. This track has markers spaced at equal distances along it from the start, as shown in the figure. The car reaches a speed of 140 km/h as it passes marker 2.
Where on the track was the car when it was traveling at half this speed, that is at 70 km/h?
- At marker 1
- Between marker 1 and marker 2
- Before marker 1
- Before marker 1
Quiz 1.1
You drive 6.0 km at 50 km/h and then another 6.0 km at 90 km/h. Your average speed over the 12 km drive will be
- equal to 70 km/h.
- exactly 38 km/h.
- It cannot be determined from the information given because we must also know directions traveled.
- greater than 70 km/h.
- less than 70 km/h.
- less than 70 km/h.
Quiz 1.1
The slope of a velocity versus time graph gives
- the distance traveled.
- displacement.
- velocity.
- acceleration.
- acceleration
Quiz 1.1
Consider a deer that runs from point A to point B. The distance the deer runs can be greater than the magnitude of its displacement, but the magnitude of the displacement can never be greater than the distance it runs.
True
False
True
Quiz 1.2
A soccer ball is released from rest at the top of a grassy incline. After 6.4 seconds the ball has rolled 91 m with constant acceleration, and 1.0 s later it reaches the bottom of the incline.
(a) What was the ball’s acceleration?
(b) How long was the incline?>
Quiz 1.2
A cart starts from rest and accelerates uniformly at 4.0 m/s2 for 5.0 s. It next maintains the velocity it has reached for 10 s. Then it slows down at a steady rate of 2.0 m/s2 for 4.0 s. What is the final speed of the car?
- 16 m/s
- 10 m/s
- 12 m/s
- 20 m/s
- 12 m/s
Quiz 1.2
A car with good tires on a dry road can decelerate (slow down) at a steady rate of about 5.0 m/s2 when braking. If a car is initially traveling at 55 mi/h
- how much time does it take the car to stop?
- what is its stopping distance?
Quiz 1.2
An airplane starts from rest and accelerates at a constant 10.8 m/s2. What is its speed at the end of a 400 m-long runway? (show your work)
Quiz 1.2
At the instant a traffic light turns green, a car that has been waiting at the intersection starts ahead with a constant acceleration of 2.00 m/s2. At that moment a truck traveling with a constant velocity of 15.0 m/s overtakes and passes the car.
- Calculate the time necessary for the car to reach the truck.
- Calculate the distance beyond the traffic light that the car will pass the truck.
- Determine the speed of the car when it passes the truck.
Quiz 1.2
Human reaction times are worsened by alcohol. How much further (in feet) would a drunk driver’s car travel before he hits the brakes than a sober driver’s car? Assume that both are initially traveling at 50.0 mi/h and their cars have the same acceleration while slowing down, and that the sober driver takes 0.33 s to hit the brakes in a crisis, while the drunk driver takes 1.0 s to do so. (5280 ft = 1 mi)
Quiz 1.3
A velocity vector has components 36 m/s westward and 22 m/s northward. What are the magnitude and direction of this vector?
Therefore, the magnitude is 42 m/s in the 31° northwest direction.
Quiz 1.3
Two displacement vectors have magnitudes of 5.0 m and 7.0 m, respectively. If these two vectors are added together, the magnitude of the sum
- is equal to 2.0 m.
- is equal to 8.6 m.
- is equal to 12 m.
- could be as small as 2.0 m or as large as 12 m.
- could be as small as 2.0 m or as large as 12 m
Quiz 1.3
If a vector A→ has components Ax < 0, and Ay < 0, then the angle that this vector makes with the positive x-axis must be in the range
- 0° to 90°
- 90° to 180°
- 180° to 270°
- 270° to 360°
- cannot be determined without additional information
- 180° to 270°
