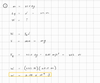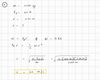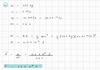Module 04: Work and Energy

Question 1

Lesson 4.1 - Work, Constant Force; Kinetic Energy, Work-Energy Principle

Define work:

Answer 1

🔬 Work: done on an object by a constant force (constant in both direction and magnitude) - the product of the magnitude of the displacement times the component of the force parallel to the displacement (scalar) SI units: joule (J)

Needs both force and displacement to work: W = F_||d

• Force negative when the force works in the opposite direction of motion
• Need to distinguish between work done by and on an object (net force)

Question 2

Lesson 4.1 - Work, Constant Force; Kinetic Energy, Work-Energy Principle

What is the formula to determine work:

Answer 2

W = F_||d

• F_|| = component of the constant for F parallel to the displacement d

W = Fd cosΘ

• F is the magnitude of the constant force
• d is the magnitude of the displacement of the object
• Θ is the angle between the direction of the force and the displacement
• No work at 90° because cos(90) = 0 so W = 0

Question 3

Lesson 4.1 - Work, Constant Force; Kinetic Energy, Work-Energy Principle

What is the Steps to solve work-related problems?

Answer 3

Draw a free-body diagram

Choose an xy coordinate system.
If the object is in motion, it may be convenient to choose one the coordinate directions as the direction of the one of the force, or as the direction of motion

Apply Newton’s Laws to determine the unknown force

Find the work done by a specific force on the object using W = Fd cosΘ

Find the net work done on the object (a) find the work done by each force and add the results (b) find the net force on an object, and then use it to find the net work done, which for constant net force is W = Fd cosΘ

Question 4

Lesson 4.1 - Work, Constant Force; Kinetic Energy, Work-Energy Principle

How do you determine the work done when there is varying force?

Answer 4

Constant force: W = Fd cosΘ

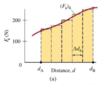
Varying Force: varies in magnitude and/or direction - REIMANN SUMS!!!!!

• Plot F|| = F cos Θ as a function of distance
• Divide the distance into small segments: Δd
• The work done is: ΔW = F_||Δd
• area of a rectangle Δd wide and F_|| hight
• Total work done is the total distance, d =d_B-d_A, is the sum of the areas of the rectangles
• Smaller segments = more accurate
• In the limit as Δd approaches zero, the total area of the many narrow rectangles approaches the area under the curve

🔬 Therefore, the work done by a variable force in moving an object between two points is equal to the area under the F|| vs. d curve between those two points.

Question 5

Lesson 4.1 - Work, Constant Force; Kinetic Energy, Work-Energy Principle

How is energy a conserved quantity?

Answer 5

Energy: is the same after any process as it was before; that is, energy is a conserved quantity. Energy is generally defined as the ability to do work.

Question 6

Lesson 4.1 - Work, Constant Force; Kinetic Energy, Work-Energy Principle

What is kinetic energy and translational kinetic energy?

Answer 6

Kinetic Energy: Energy of motion (object in motion has the ability to do work and thus has energy)

Define the quality 1/2mv² to be the translational kinetic energy (KE) of the objects:

KE = 1/2 mv²

1. Directly proportional to the mass of the object
2. Directly proportional to the square of the speed

Question 7

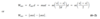
Lesson 4.1 - Work, Constant Force; Kinetic Energy, Work-Energy Principle

What is the Work-Energy Principle?

Answer 7

Work-Energy Principle: The net work done on an object is equal to the change in the object’s kinetic energy

• Only valid if W is the net work done on the object (all forces acting on the object)

W_net = KE₂ - KE₁

or

W_net = ΔKE = 1/2mv₂² - 1/2mv₁²

Question 8

Define potential energy:

Answer 8

🔬 Potential Energy:
Energy is associated with forces that depend on the position or configuration of an object relative to the surroundings

Question 9

Lesson 4.2 - Potential Energy

Define Gravitational Potential Energy:

Answer 9

Gravitational Potential Energy: Product of the object’s weight and its height above some reference level (like the ground)

PE_G = mgy

Question 10

Lesson 4.2 - Potential Energy

How does gravitational potential energy work for the following system?

Answer 10

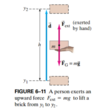
For an object of mass m to be lifted vertically, upwards force at least equal to the weight (mg) must be exerted on the object.

• Lift without acceleration: exertes an “external force”: F_ext = mg
• Work = Force * dispalcement (vertical)
• Therefore: W_ext = F_extd cosΘ = mgh*cos180°
• Gravity is also acting on the object as it moves from y2 to y1: W_G = F_GdcosΘ=mgh*cos180°, where Θ = 180 because F and d are pointing in opposite directions:
• W_G = -mgh = -mg(y₂-y₁)*
• Raise an object of mass m to a height h, you need an amount of work equal to mgh.
• Once at height h, the object has the ability to do the amount of work = mgh

🔬 Gravitational Potential Energy: Product of the object’s weight and its height above some reference level (like the ground)

PE_G=mgy

Question 11

Lesson 4.2 - Potential Energy

What is a change in gravitational potential energy and how does it relate to work done?

Answer 11

Higher the object, the more gravitational potential energy it has:

W_ext = mg(y₂-y₁)=PE₂-PE₁=ΔPE_G

When an object is moved from y1 to y2 = the work done by the net external force needed to move the object

Hence, a change in gravitational potential energy: equal to the negative of the work done by gravity

W_G = -mg(y₂-y₁)

W_G = -(PE₂-PE₁) = -ΔPE_G

ΔPE_G = -W_G

Question 12

Lesson 4.2 - Potential Energy

What is a change in potential energy (in general)?

Answer 12

A change in potential energy associated with a particular force = to the negative of the work done by that force when the object is moved from one point to a second point.

(Or) Work required a net external force to move the object without acceleration between two points.

Question 13

Lesson 4.2 - Potential Energy

How is external and restoring force acting on this string?

What is the potential energy of the elastic string?

Answer 13

Potential energy when compressed

• When released - does work on the object
• Stretch or compress a string x amount from its natural (unstretched) length required external force on the spring of magnitude F(ext)
• F(ext) is directly proportional to x.

F_(ext) = kx

• k = spring stiffness constant (spring constant)

Resorting Force:

• Stretched or compressed itself exerts force, F(s), in the opposite direction on the hand
• Exerts force in the direction opposite the displacement
• String equation or Hooke’s Law:

F_s = -kx

Question 14

Lesson 4.2 - Potential Energy

What is Hooke’s Law?

Answer 14

• Stretched or compressed itself exerts force, F(s), in the opposite direction on the hand
• Exerts force in the direction opposite the displacement
• String equation or Hooke’s Law:

F_s = - kx

Question 15

Lesson 4.2 - Potential Energy

How do you calculate the potential energy of a string?

Answer 15

• F_(ext) varies over distance x, from zero at the unstretched position to kx
• Use average force F: F =1/2[0+kx]=1/2xk (where x is the total amount stretched)
• When work is done: W_(ext) = Fx= (1/2kx)(x) = 1/2kx²
• Hence, elastic potential energy (PE_(el)) is proportional to the square of the amount stretched:

PE_(el)=1/2kx²

• x can be the amount compressed or stretched from the natural (equilibrium) length

Question 16

Lesson 4.2 - Potential Energy

What are conservative Forces?

Answer 16

🔬 Conservative Forces: Gravity does not depend on the path taken but on the initial and final position

• Elastic forces are also conservative
• Work done against gravity in moving an object does not depend on the path taken
• Potential energy can only be defined for a conservative force and not all forces have potential energy

Question 17

Lesson 4.2 - Potential Energy

What are nonconservative forces?

Answer 17

🔬 Nonconservative Forces: (Friction and a push or pull) Since any work they do depends on the path.

Push a crate straight or curved changes the amount of work done

• Curved path is longer so required more work

Question 18

Lesson 4.2 - Potential Energy

What forces are conservative and which are neoconservative?

Answer 18

Question 19

Lesson 4.2 - Potential Energy

Hows does potential energy relate to conservative and neoconservative forces?

Answer 19

Potential energy can only be defined for a conservative force and not all forces have potential energy

Question 20

Lesson 4.2 - Potential Energy

How does the Work-Energy Principle relate to potential energy?

Answer 20

• Total (net) work as a sum of the work done by conservative forces, Wc, and the work done by nonconservative forces, Wnc:
• W_(net) = W_c+W_Nc *
• Then: W(net) = ΔKE and Wc + Wnc = ΔKE
• Conservative forces can be written in form of potential energy: Wc = -ΔPE

Therefore:

W_Nc=ΔKE + ΔPE

🔬 The Work done Wnc done by the neoconservative force is equal to the total change in kinetic and potential energies

Question 21

Lesson 4.3 - Conservation of Mechanical Energy

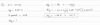
What is the Total Mechanical Energy (E) of a system?

Answer 21

Total Mechanical Energy (E) of a system as the sum of kinetic and potential energies at any moment:

KE₂+PE₂ = KE₁+PE₁

or

E₂=E₁=constant

Conserved Quantity: The total mechanical energy remains constant as long as no neoconservative forces do work

Question 22

Lesson 4.3 - Conservation of Mechanical Energy

What is the Principle of Conservation of Mechanical Energy?

Answer 22

🔬 Principle of Conservation of Mechanical Energy:

If only conservative forces do work, the total mechanical energy of a system neither increases nor decreases in any process. So its constant - conserved

Question 23

Lesson 4.3 - Conservation of Mechanical Energy

What is Total Mechanical Energy at any point in time?

Answer 23

E=KE+PE=1/2mv²+mgy

• When total mechanical energy at point 1 = total mechanical energy at point 2:

1/2mv²₁+mgy₁=1/2mv²₂+mgy²

Question 24

Lesson 4.4 - Law of Conservation of Energy

What is the Law of Conversation of Energy?

Answer 24

🔬 Law of Conversation of Energy: The total energy is neither increasing nor decreasing in any process. Energy can be transformed from one form to another, and transferred from one object to another, but the total amount remains constant

• Work is done when energy is transferred from one object to another

Question 25

Lesson 4.4 - Law of Conservation of Energy

How does the natural world deviate from the Law of Conservation of Energy?

Answer 25

In other natural processes, the mechanical energy (sum of kinetic and potential energies) does not remain constant but decreases

Frictional forces reduce the mechanical energy (not total energy) - called Dissipative Forces

Question 26

Lesson 4.4 - Law of Conservation of Energy

How do the work-energy principle and energy conservation result in an equation for friction?

Answer 26

• Work-Energy Particle: W_Nc = ΔKE + ΔPE
• If one object moves from one point to another: W_Nc = KE2 - KE1 + PE2 - PE1
• Which means that: KE1 + PE1 + Ecn = KE2 + PE2

Therefore, for friction:

W_Nc = -F_frd

• d is the distance over which the friction (constant) acts
• KE = 1/2mc² and PE = mgy

W_Nc = -F_frd:

1/2mv²₁+mgy₁-Ffrd=1/2mv₂²+mgy₂

Thus, the initial mechanical energy is reduced by the amount F_frd:

• State equally well that the initial mechanical energy = the (reduced) final mechanical energy

Question 27

Lesson 4.4 - Law of Conservation of Energy

When should you apply the Energy Conservation Law and when the Work-Energy Principle?

Answer 27

Law of Conservation is more general and powerful than the work-energy principle

Work-Energy Principle: Rigid object on which external force work (external forces = change in its kinetic energy)

Law of Conservation: Which no external force do work

Question 28

Lesson 4.4 - Law of Conservation of Energy

When do you use Newton’s Laws compared to work-and-energy?

Answer 28

If the force(s) are constant = either works

If the forces are not constant and/or the path is not simple = energy may be better (it is a scalar)

Question 29

Lesson 4.5 - Power

Define Power:

Answer 29

Rate at which work is done or the rate at which energy is transformed (watt [W])

Question 30

Lesson 4.5 - Power

What is average power?

Answer 30

P = average power = work / time = energy transformed / time

Question 31

Lesson 4.5 - Power

What is horsepower?

Answer 31

1 hp = 55 ft * bl/s = 746 W

Question 32

Lesson 4.5 - Power

What is Power in terms of force applied to an object and its speed v?

Answer 32

• P = W/t
• W = Fd

Hence:

P=W/t = Fd/t = Fv

Question 33

Lesson 4.5 - Power

What is efficiency?

Answer 33

The ratio of the useful power output of an engine e, P(out), to the power input, P(in):

e = P_out / P_in

• always less than 1 (no engine can create energy, and no engine can even transform energy from one form to another without some energy going to friction, thermal energy, and other non-useful energies
• Car engine has roughly about 15% efficiency

Question 34

Lesson 4.1 Questions

1. (I) A 75.0-kg fire fighter climbs a flight of stairs 28.0 m high. How much work does he do?

Answer 34

Question 35

Lesson 4.1 Questions

3. (II) How much work did the movers do (horizontally) pushing a 46.0-kg crate 10.3 m across a rough floor without acceleration, if the effective coefficient of friction was 0.50?

Answer 35

Question 36

Lesson 4.1 Questions

5. (II) What is the minimum work needed to push a 950-kg car 710 m up along a 9.0° incline? Ignore friction.

Answer 36

Question 37

Lesson 4.1 Questions

15. (I) At room temperature, an oxygen molecule, with mass of 5.31 ´ 10^-26 kg, typically has a kinetic energy of about 6.21 ´ 10^–21 J. How fast is it moving?

Answer 37

Question 38

Lesson 4.1 Questions

17. (I) How much work is required to stop an electron (m = 9.11 ´ 10^-31 kg) which is moving with a speed of 1.10 ´ 10⁶ m/s?

Answer 38

Question 39

Lesson 4.1 Questions

19. (II) Two bullets are fired at the same time with the same kinetic energy. If one bullet has twice the mass of the other, which has the greater speed and by what factor? Which can do the most work?

Answer 39

Question 40

Lesson 4.1 Questions

21. (II) An 85-g arrow is fired from a bow whose string exerts an average force of 105 N on the arrow over a distance of 75 cm. What is the speed of the arrow as it leaves the bow?

Answer 40

Question 41

Lesson 4.2 Questions

27. (I) A spring has a spring constant k of 88.0 N/m. How much must this spring be compressed to store 45.0 J of potential energy?

Answer 41

Question 42

Lesson 4.2 Questions

29. (II) A 66.5-kg hiker starts at an elevation of 1270 m and climbs to the top of a peak 2660 m high. (a) What is the hiker’s change in potential energy? (b) What is the minimum work required of the hiker? (c) Can the actual work done be greater than this? Explain.

Answer 42

Question 43

Lesson 4.3 Question

31. (I) A novice skier, starting from rest, slides down an icy frictionless 8.0° incline whose vertical height is 105 m. How fast is she going when she reaches the bottom?

Answer 43

Question 44

Lesson 4.3 Question

33. (II) A sled is initially given a shove up a frictionless 23.0° incline. It reaches a maximum vertical height 1.22 m higher than where it started at the bottom. What was its initial speed?

Answer 44

Question 45

Lesson 4.3 Question

* 35. (II) A spring with k = 83 N/m hangs vertically next to a ruler. The end of the spring is next to the 15-cm mark on the ruler. If a 2.5-kg mass is now attached to the end of the spring, and the mass is allowed to fall, where will the end of the spring line up with the ruler marks when the mass is at its lowest position?

Answer 45

Question 46

Lesson 4.3 Question

37. (II) A 1200-kg car moving on a horizontal surface has speed v = 85 km/h when it strikes a horizontal coiled spring and is brought to rest in a distance of 2.2 m. What is the spring stiffness constant of the spring?

Answer 46

Question 47

Lesson 4.3 Question

39. (II) A vertical spring (ignore its mass), whose spring constant is 875 N/m, is attached to a table and is compressed down by 0.160 m. (a) What upward speed can it give to a 0.380-kg ball when released? (b) How high above its original position (spring compressed) will the ball fly?

Answer 47

Question 48

Lesson 4.4 Questions

47. (I) A 16.0-kg child descends a slide 2.20 m high and, starting from rest, reaches the bottom with a speed of 1.25 m/s. How much thermal energy due to friction was generated in this process?

Answer 48

Question 49

Lesson 4.4 Questions

* 49. (II) A 145-g baseball is dropped from a tree 12.0 m above the ground. (a) With what speed would it hit the ground if air resistance could be ignored? (b) If it actually hits the ground with a speed of 8.00 m/s, what is the average force of air resistance exerted on it?

Answer 49

Question 50

Lesson 4.4 Questions

51. (II) A skier traveling 11.0 m/s reaches the foot of a steady upward 19° incline and glides 15 m up along this slope before coming to rest. What was the average coefficient of friction?

Answer 50

Question 51

Lesson 4.4 Questions

53. (II) A 66-kg skier starts from rest at the top of a 1200-m long trail which drops a total of 230 m from top to bottom. At the bottom, the skier is moving 11.0 m/s. How much energy was dissipated by friction?

Answer 51

Question 52

Lesson 4.5 Questions

57. (I) How long will it take a 2750-W motor to lift a 385-kg piano to a sixth-story window 16.0 m above?

Answer 52

Question 53

Lesson 4.5 Questions

59. (I) An 85-kg football player traveling 5.0 m/s is stopped in 1.0 s by a tackler. (a) What is the original kinetic energy of the player? (b) What average power is required to stop him?

Answer 53

Question 54

Lesson 4.5 Questions

61. (II) An outboard motor for a boat is rated at 35 hp. If it can move a particular boat at a steady speed of 35 km/h, what is the total force resisting the motion of the boat?

Answer 54

Question 55

Lesson 4.5 Questions

63. (II) A driver notices that her 1080-kg car, when in neutral, slows down from 95 km/h to 65 km/h in about 7.0 s on a flat horizontal road. Approximately what power (watts and hp) is needed to keep the car traveling at a constant 80 km/h?

Answer 55

Question 56

Lesson 4.5 Questions

65. (II) A 975-kg sports car accelerates from rest to 95 km/h in 6.4 s. What is the average power delivered by the engine?

Answer 56

Question 57

Lesson 4.5 Questions

67. (II) A pump lifts 27.0 kg of water per minute through a height of 3.50 m. What minimum output rating (watts) must the pump motor have?

Answer 57

Question 58

A person stands on the edge of a cliff. She throws three identical rocks with the same speed. Rock X is thrown vertically upward, rock Y is thrown horizontally, and rock Z is thrown vertically downward. If the ground at the base of the cliff is level, which rock hits the ground with the greatest speed if there is no air resistance?

1. Rock Y
2. They all hit the ground with the same speed.
3. Rock Z
4. Rock X

Answer 58

2. They all hit the ground with the same speed

All three rocks start at the same height, so they have the same potential energy. They also start with the same speed (even though they’re in different directions), so they have the same kinetic energy.

Energy is conserved, so when they land, all the potential energy is converted into kinetic energy. Therefore, they must all have the same speed (though not necessarily the same direction).

Question 59

Module 04 Exam

Two men, Joel and Jerry, push against a car that has stalled, trying unsuccessfully to get it moving. Jerry stops after 10 min, while Joel is able to push for 5.0 min longer. Compare the work they do on the car.

1. Joel does 50% more work than Jerry.
2. Jerry does 50% more work than Joel.
3. Joel does 25% more work than Jerry.
4. Joel does 75% more work than Jerry.
5. Neither of them does any work.

Answer 59

5. Neither of them does any work

Question 60

Module 04 Exam

Two objects, one of mass m and the other of mass 2m, are dropped from the top of a building. If there is no air resistance, when they hit the ground

1. the heavier one will have twice the kinetic energy of the lighter one.
2. both will have the same kinetic energy.
3. the heavier one will have four times the kinetic energy of the lighter one.
4. the heavier one will have half the kinetic energy of the lighter one.
5. the heavier one will have one-fourth the kinetic energy of the lighter one.

Answer 60

1. the heavier one will have twice the kinetic energy of the lighter one

Question 61

Module 04 Exam

A lightweight object and a very heavy object are sliding with equal speeds along a level frictionless surface. They both slide up the same frictionless hill with no air resistance. Which object rises to a greater height?

1. The heavy object, because it has more mass to carry it up the hill.
2. The heavy object, because it has greater initial kinetic energy.
3. They both slide to exactly the same height.
4. The light object, because gravity slows it down less.
5. The lightweight object, because the force of gravity on it is less.

Answer 61

3. They both slide to exactly the same height

Question 62

Module 04 Exam

A person stands on the edge of a cliff. She throws three identical rocks with the same speed. Rock X is thrown vertically upward, rock Y is thrown horizontally, and rock Z is thrown vertically downward. If the ground at the base of the cliff is level, which rock hits the ground with the greatest speed if there is no air resistance?

Rock Y

They all hit the ground with the same speed.

Rock Z

Rock X

Answer 62

They all hit the ground with the same speed.

Question 63

Module 04 Exam

If a stone is dropped with an initial gravitational potential energy of 100 J but reaches the ground with a kinetic energy of only 75 J, this is a violation of the principle of conservation of energy.

True or False

Answer 63

False

Question 64

Module 04 Exam

Jill does twice as much work as Jack does and in half the time. Jill’s power output is

1. twice Jack’s power output.
2. one-fourth as much as Jack’s power output.
3. the same as Jack’s power output.
4. one-half as much as Jack’s power output.
5. four times Jack’s power output.

Answer 64

5. four times Jack’s power output

Question 65

Module 04 Exam

A force produces power P by doing work W in a time T. What power will be produced by a force that does six times as much work in half as much time?

Answer 65

12 P

Question 66

Module 04 Exam

A very light ideal spring with a spring constant (force constant) of 2.5 N/cm pulls horizontally on an 18-kg box that is resting on a horizontal floor. The coefficient of static friction between the box and the floor is 0.65, and the coefficient of kinetic friction is 0.45.

(a) How long is the spring just as the box is ready to move?
(b) If the spring pulls the box along with a constant forward velocity of 1.75 m/s, how long is the spring?
(c) How long is the spring if it pulls the box forward at a constant 2.75 m/s?

Answer 66

(a) 46 cm (b) 32 cm (c) 32 cm

Question 67

Module 04 Exam

You carry a 7.0-kg bag of groceries above the ground at constant speed across a room. How much work do you do on the bag in the process?

Answer 67

0 J

Question 68

Module 04 Exam

A 30-N box is pulled upward 6.0 m along the surface of a ramp that rises at 37° above the horizontal. How much work does gravity do on the box during this process?

Answer 68

-110 J

Question 69

Module 04 Exam

A 2.0-kg object is lifted vertically through 3.00 m by a 150-N force. How much work is done on the object by gravity during this process?

Answer 69

Question 70

Module 04 Exam

How much kinetic energy does a 0.30-kg stone have if it is thrown at 44m/s?

Answer 70

290 J

Question 71

Module 04 Exam

How much work must be done by frictional forces in slowing a 1000-kg car from 26.1m/s to rest?

Answer 71

3.41 × 10⁵ J

Question 72

Module 04 Exam

On an alien planet, an object moving at 4.0 m/s on the horizontal ground comes to rest after traveling a distance of 10 m. If the coefficient of kinetic friction between the object and the surface is 0.20, what is the value of g on that planet?

Answer 72

4.0 m/s²

Question 73

Module 04 Exam

The kinetic friction force that a horizontal surface exerts on a 60.0-kg object is 50.0 N. If the initial speed of the object is 25.0 m/s, what distance will it slide before coming to a stop?

Answer 73

375 m

Question 74

Module 04 Exam

How high a hill would a 75-kg hiker have to climb to increase her gravitational potential energy by 10,000 J?

Answer 74

Question 75

Module 04 Exam

You want to store 1,000 J of energy in an ideal spring when it is compressed by only 2.5 cm. What should be the force constant (spring constant) of this spring?

Answer 75

Question 76

Module 04 Exam

If the work done to stretch an ideal spring by 4.0 cm is 6.0 J, what is the spring constant (force constant) of this spring?

Answer 76

7500 N/m

Question 77

Module 04 Exam

An ideal spring with a force constant (spring constant) of 15 N/m is initially compressed by 3.0 cm from its uncompressed position. How much work is required to compress the spring an additional 4.0 cm?

Answer 77

0.030 J

Question 78

Module 04 Exam

In the figure, a ball hangs by a very light string. What is the minimum speed of the ball at the bottom of its swing (point B) in order for it to reach point A, which is 1.0 m above the bottom of the swing?

Answer 78

4.4 m/s

Question 79

Answer 79

-1.8 J

Question 80

Module 04 Exam

A sled is moving along a horizontal surface with a speed of 5.7 m/s. It then slides up a rough hill having a slope of 11° above the horizontal. The coefficient of kinetic friction between the sled and the surface of the hill is 0.26. How far along the surface does the block travel up the incline?

Answer 80

Question 81

Module 04 Exam

The figure shows two crates, each of mass m = 24 kg, that are connected by a very light wire. The coefficient of kinetic friction between the crate on the inclined surface and the surface itself is 0.31. Find the speed of the crates after they have moved 1.6 m starting from rest.

Answer 81

Question 82

Module 04 Exam

As shown in the figure, a 4.0-kg block is moving at 5.0 m/s along a horizontal frictionless surface toward an ideal spring that is attached to a wall. After the block collides with the spring, the spring is compressed a maximum distance of 0.68 m. What is the speed of the block when the spring is compressed to only one-half of the maximum distance?

Answer 82

Question 83

Module 04 Exam

How many joules of energy are used by a 1.0-hp motor that runs for 1.0 hour? (1 hp = 746 W)

Answer 83

2.7 MJ

Question 84

Module 04 Exam

A typical incandescent light bulb consumes 75 W of power and has a mass of 30 g. You want to save electrical energy by dropping the bulb from a height great enough so that the kinetic energy of the bulb when it reaches the floor will be the same as the energy it took to keep the bulb on for 1.0 hour. From what height should you drop the bulb, assuming no air resistance and constant g?

Answer 84

Question 85

Module 04 Exam

Suppose you left five 100-W light bulbs burning in the basement for two weeks. If electricity costs 10.0¢/kW∙h, (a) how much did the electricity cost (to the nearest dollar) to leave those bulbs on, and (b) how many joules of electrical energy did they consume?

Answer 85

Question 86

Module 04 Exam

In a physical fitness program, a woman who weighs 510 N runs up four flights of stairs in 22 s. Each flight rises 3.1 m. (1 hp = 746 W)

(a) What is her total change in potential energy?
(b) What was the minimum average power (in watts) that she expended during the 22 s?
(c) What horsepower motor would be required to generate the same power?

Answer 86

(a) 6.3 kJ (b) 290 W (c) 0.39 hp

Question 87

Module 04 Exam

A sand mover at a quarry lifts 2,000 kg of sand per minute a vertical distance of 12 m. The sand is initially at rest and is discharged at the top of the sand mover with speed 5.0 m/s into a loading chute. What minimum power must be supplied to this machine?

6. 7 kW
7. 9 kW
8. 3 kW

520 W

1.1 kW

Answer 87

NOT 3.9 kW