Kinetics 4: Complex reactions: pre-equilibrium, steady state, MM Flashcards
Define an elementary step.
An elementary step is a single reactive encounter between species – is the smallest unit of a reaction.
Define (kinetic) mechanism.
A proposed set of elementary steps accounting for the features of a reaction.
Define an elementary reaction
Consists of a single elementary step
Elementary reaction: Cl + O2 –> ClO + O, with rate constant k
Write the rate of change for each species.
elementary reaction means rate laws can be taken directly from eq since everything is simultaneous
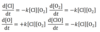
The complex reaction below occurs in 2 elementary steps. Write the rate of change of:
- product
- carbocation
- to calculate how [P] changes with time, the diff eqs must be integrated, which is possible here but gets complex as more steps are added, since a given variable appears in multiple eqs.*
- Hard to solve w/o computer, so the following methods remove some of the complex time-dependence by making assumptions about the relative rates of processes.*
Two sequential, first-order reactions, with rate constants k1 and k2:
A –> B (1) B –> C (2)
Suppose k1 << k2. Draw conc of each species against time on the same axes, and state which step is rate-determining.
1 is the RDS
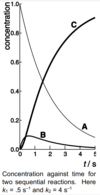
process 1 has smaller rate constant therefore slower
Two sequential, first-order reactions, with rate constants k1 and k2:
A –> B (1)
B –> C (2)
Suppose k1 >> k2. Draw conc of each species against time on the same axes, and state which step is rate-determining.
2 is the RDS
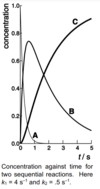
process 2 has smaller rate constant therefore slower
Study the reaction scheme below. What conditions are required for the pre-equilibrium hypothesis to apply?
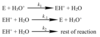
- Rate of process 1 >> rate of process 2
- Such that rates of [1] and [-1] are equal (i.e. equilibrium is established between E, H3O+ and EH+)
- And therefore process [2] is rate-determining
pre-eq hypothesis is often useful for intermediates involving protonation or deprotonation, since these processes are usually faster than breaking/making bonds to atoms heavier than hydrogen
Study the reaction scheme below. Use the pre-equilibrium hypothesis to derive an expression for the rate equation for formation of products.
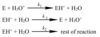
Rate of process 1 >> rate of process 2, such that rates of [1] and [-1] are equal (in equilibrium), and process [2] is rate-determining:
k1[E][H3O]+ = k-1[EH+][H2O]
So [EH]+ = (k1/k-1)([E][H3O]+/[H2O])
= keq([E][H3O]+/[H2O])
r = d[P]/dt = k2[EH+][H2O]
= k2keq([E][H3O]+)
- pre-eq hypothesis makes final rate eq simpler since it involves only reactants, so can be integrated as in previous sections*
- Could then find experimentally that rate = kexp([E][H3O]+/[H2O]) – comparing with theoretical rate law would show kexp is a composite of the rate constants of 3 steps*
What conditions permit using the steady state approximation? Include a graph of concentration against time.
Applicable when, in a complex mechanism, a reactive intermediate reacts as soon as it’s formed, such that its concentration is assumed to be constant.
Only applicable when reaction is in steady state - not in the initial or final phases.
simplifies solving differential eqs since it removes the time dependence
Consider the sequential reaction A –> B –> C with rate constants k1 and k2.
Use the steady state approximation to derive an expression for the rate of product formation.
as expected, eq indicates B reacts as soon as it’s formed, such that the first step of the reaction is the RDS.
In the reaction scheme below, EH+ is assumed to be in the steady state. Derive an expression for the rate of formation of products.
r = d[P]/dt = ((k1k2)/(k1+k2)) x [E][H3O]+
general process
- identify the intermediate(s)
- write the rate law for each, each reaction producing/consuming the intermediate contributes a term to the expression, those consuming it give negative terms
- set this = 0
- rearrange for [intermediate]ss
- write rate law for products, sub in [intermediate], simplify
In the reaction scheme below, EH+ is assumed to be in the steady state. The rate of formation of products is given by:
r = d[P]/dt = ((k1k2)/(k1+k2)) x [E][H3O]+
Suppose the rate of [2] >> that of [-1]. Simplify the expression.
k2[EH+][H2O] >> k-1[EH+][H2O]
Therefore k2 >> k1
Approximate denominator (k1+k2) = k2
So rate law becomes
r = d[P]/dt = ((k1k2)/(k2)) x [E][H3O]+
= k1[E][H3O]+
reaction is effectively 2 sequential steps (since -1 is negligable), with the first being slower, so rate depends on [1] only since it’s the RDS
In the reaction scheme below, EH+ is assumed to be in the steady state. The rate of formation of products is given by:
r = d[P]/dt = ((k1k2)/(k-1+k2)) x [E][H3O]+
Suppose the rate of [-1] >> that of [2]. Simplify the expression.
k2[EH+][H2O] << k-1[EH+][H2O]
Therefore k2 << k-1
Approximate denominator (k-1+k2) = k-1
So rate law becomes
r = d[P]/dt = ((k1k2)/(k-1)) x [E][H3O]+
= keqk2[E][H3O]+
NB identical to rate law derived assuming [1] and [-1] form a pre-equilibrium. this is since assuming that rate of [-1] >> [2] assumes an equilibrium is set up, and that [2] is a slow RDS, ie bleeding off of EH+
try page 36 on notes, decomposition of N205
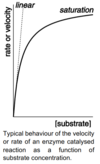
What is saturation kinetics?
Where, for a fixed quantity of enzyme, as [S] increases, the rate of reaction first increases linearly, then levels off to a limiting maximum value.
Write out the Michaelis-Menten scheme.
Shown is the Michaelis-Menten scheme.
- Give the expression for KM
- What units does it have?
- define it
kM = (k-1 + kcat)/k1)
Units of conc
KM is the substrate conc which gives ha;f-maximum velocity.
Shown is the Michaelis-Menten scheme.
Write the Michaelis-Menten equation, i.e. the expression for the velocity, V (ie rate) of reaction.
V = (kcat[E]0[S]) / ([S] + (k-1 + kcat)/k1)
= (kcat[E]0[S]) / ([S] + kM)
where KM is the michaelis constant
Shown is the Michaelis-Menten scheme.
Using the steady state approximation, derive the Michaelis-Menten equation, ie the expression for the velocity, V (ie rate) of reaction.
Assume ES in steady state since intermediate
So d[ES]/dt = k1[E][S] - k-1[ES] -kcat[ES] = 0
Derive an expression for [E], then plug into the above (so that [ES] is the only unknown, given [E]0 is known)
[E]0 = [ES] + [E] –> [E] = [E]0 - [ES]
k1([E]0 - [ES])[S] - k-1[ES] -kcat[ES] = 0
Rearrange for [ES]
[ES]ss = (k1[E]0[S])/(k1[S]+ k-1 + kcat)
Plug [ES] into the expression for velocity (rate)
d[P]/dt = V = kcat[ES]
= (kcatk1[E]0[S])/(k1[S]+ k-1 + kcat)
divide through by k1
V = (kcat[E]0[S]) / ([S] + (k-1 + kcat)/k1)
= (kcat[E]0[S]) / ([S] + kM)
where KM is the michaelis constant
Shown is the Michaelis-Menten equation.
V = (kcat[E]0[S]) / ([S] + kM)
Dependence of V on [S] is complex, so V is measured for the initial rate.
When substrate conc is low:
- Simplify the equation
- State the order of reaction in [S] and [E]0
- State the rate constant and its order
- Give the biological interpretation
[S] << KM so simplify denominator:
V = (kcat[E]0[S]) / kM
1st order in [S] and [E]0
2nd order rate constant kcat/KM
There is more free enzyme than substrate-bound enzyme, so rate is limited by substrate availability, hence first order in [S].
Shown is the Michaelis-Menten scheme.
Write the expression for Vmax and define it.
Vmax = kcat[E]0
Maximum velocity which occurs when all enzyme is saturated, i.e. 0 order in [S].
Shown is the Michaelis-Menten equation.
V = (kcat[E]0[S]) / ([S] + kM)
Dependence of V on [S] is complex, so V is measured for the initial rate.
When substrate conc is high:
- Simplify the equation
- State the order of reaction in [S] and [E]0
- State the rate constant and its order
- Give the biological interpretation
- State the RDS
[S] >> KM so simplify denominator:
V = (kcat[E]0[S]) / [S] = kcat[E]0 = Vmax
0 order in [S], 1st order in [E]0
1st order rate constant kcat
Velocity is independent of S, due to saturation of V: enzymes all substate-bound so adding S has no effect.
RDS = ES –> E+ P
Shown is the Michaelis-Menten equation.
V = (kcat[E]0[S]) / ([S] + kM)
Substitute in the expression for Vmax and use this to interpret the meaning of Km.
Vmax = kcat[E]0
V = (Vmax[S]) / ([S] + kM)
Substate conc [S]1/2 results in half the max velocity
Vmax/2 = (Vmax[S]1/2) / ([S]1/2 + KM)
So 1/2 = ([S]1/2) / ([S]1/2 + KM)
So ([S]1/2 + KM) = 2[S]1/2
Thus [S]1/2 = KM
So KM is the substrate conc which gives half-maximum velocity.
What is the interpretation of large and small KM?
- Large Km: large [S] is needed to achieve half-maximum rate, since enzyme has weak affinity for substrate
- Small Km: little [S] is needed to achieve half-maximum rate, since enzyme has strong affinity for substrate
Shown is the Michaelis-Menten equation.
V = (kcat[E]0[S]) / ([S] + kM)
Show how it can give a straight-line plot, and state the intercept and slope (give the version not using, and the one using, Vmax).
V = (kcat[E]0[S]) / ([S] + kM)
1/V = ([S] + kM) / (kcat[E]0[S])
= KM/(kcat[E]0) x (1/[S]) + 1/(kcat[E]0)
Plot 1/V against 1/[S], giving straight line with slope KM/(kcat[E]0) and intercept 1/(kcat[E]0)
Vmax version
recall Vmax = [S][E]0
V = (kcat[E]0[S]) / ([S] + kM)
1/V = ([S] + kM) / (kcatVmax)
= (KM/Vmax)(1/[S]) + 1/Vmax
Plotting 1/V against 1[S] gives a straight line with slope (KM/Vmax) and intercept 1/Vmax
Shown is the Michaelis-Menten equation.
V = (kcat[E]0[S]) / ([S] + kM)
Plotting 1/V against 1/[S] gives a straight line with slope KM/(kcat[E]0) and intercept 1/(kcat[E]0), or a straight line with slope (KM/Vmax) and intercept 1/Vmax.
Why are these double-reciprocal plots prone to error?
Error in low [S] values are magnified, since in this region 1/[S] is high. So the position of the line, and thus the slope and intercept used to deduce kcat and KM, is overly influenced by these low [S] values.
