Energetics & Equilibria 2: Gibbs energy

Question 1

• Definition of Gibbs energy, G (eq)
• Give its unit

Answer 1

• G = H - TS
• kJ mol^-1 (since it’s a measure of energy)

this quantity allows you to just consider the system at hand, rather than the universe

Question 2

What is true of G, for constant temp and pressure,

• during a spontaneous process?
• at eq?

Answer 2

Spontaneoous: ΔG < 0 (G decreases)

Eq: ΔG = 0 (G is at a mimimum)

Question 3

Show that G decreases for a spontaneous process, and ΔG = 0 at equilibrium.

Answer 3

First consider G

Definition of G

G = H_sys - T_sysS_sys

Complete differential, then use product rule:

dGsys = dH_sys + d(-T_sysS_sys) = dH_sys - T_sysdS_sys - S_sysdT_sys

At constant temp, S_sysdT_sys = 0, so:

dG_sys = dH_sys -T_sysdS_sys (constant temp)

• Divide both sides by -T*
• dG_sys/T_sys = -dH_sys/T_sys + dS_sys (constant temp)

Then consider entropy

Recall ΔS_univ = ΔS_surr + ΔS_sys = -q_sys/T_surr + ΔS_sys

Differential form:

dS_univ = - δq_sys/T_surr + dS_sys

At constant pressure, δq_sys = dH_sys. And system and surroundings are at same temp, so:

dS_univ = - dH_sys/T_sys + dS_sys (constant pressure)

Then combine them (and their conditions)

-dG_sys/T = dS_univ (constant temp and pressure)

Conclusions

• In a spontaneous process, S_univ increases, so dS_univ is positive, so, for constant temp, dG_sys must be negative, so ΔG < 0. So G falls
• At equilibrium (reversible process), dS_univ = 0, so dS_univ = 0, so dG_sys = 0, so ΔG = 0. So G is at a minimum

Question 4

show how to get from

G = H_sys - T_sysS_sys

to

ΔG = ΔH - TΔS (constant temp and pressure)

Answer 4

Definition of G

G = H_sys - T_sysS_sys

Complete differential, then use product rule:

dGsys = dH_sys + d(-T_sysS_sys) = dH_sys - T_sysdS_sys - S_sysdT_sys

At constant temp, S_sysdT_sys = 0, so:

dG_sys = dH_sys -T_sysdS_sys (constant temp and pressure)

Write in terms of finite changes (rather than infinitesimal)

ΔG_sys = ΔH_sys - TΔS_sys (constant temp and pressure)

Drop sys subscripts since it’s implied that we’re discussing system

ΔG = ΔH - TΔS (constant temp and pressure)

Question 5

When is it true that dU = δq - pdV?

Answer 5

The only work done is that of gas expansion:

dU = δq - pdV (pV work only)

Question 6

Give the first, second and third master equations

Answer 6

dU = TdS - pdV

dH = TdS + Vdp

dG = VdP - SdT

Question 7

1. Derive the first master equation:

dU = TdS - pdV

2. Explain why it’s true for both reversible and irreversible processes

Answer 7

1.

dU = δq - δw

dU = δq - pdV (pV / gas expansion work only)

Assume reversible

dU = δq_rev - pdV

dS = δq_rev/T

δq_rev = TdS

Combine eq

dU = TdS - pdV

2. True for all changes since U is a state function. When reversible, δq = TdS and δw = pdV. When irreversible, this isn’t true, but their stum still = dU.

Question 8

Derive the second master equation:

dH = TdS + Vdp

Answer 8

Derive the first one:

dU = δq - δw

dU = δq - pdV (pV / gas expansion work only)

Assume reversible

dU = δq_rev - pdV

dS = δq_rev/T

δq_rev = TdS

Combine eq

dU = TdS - pdV

Use this to derive the second

• Definition of enthalpy:* H = U + pV
• Complete differential, then product rule:*

dH = dU + d(pV) = dU + pdV + Vdp

Sub in first eq

dH = (TdS - pdV) + pdV + Vdp

dH = TdS + Vdp

Question 9

Derive the third master equation:

dG = Vdp - SdT

Answer 9

Derive the first one:

dU = δq - δw

dU = δq - pdV (pV / gas expansion work only)

Assume reversible

dU = δq_rev - pdV

dS = δq_rev/T

δq_rev = TdS

Combine eq

dU = TdS - pdV

Use this to derive the second

• Definition of enthalpy:* H = U + pV
• Complete differential, then product rule:*

dH = dU + d(pV) = dU + pdV + Vdp

Sub in first eq

dH = (TdS - pdV) + pdV + Vdp

dH = TdS + Vdp

Then derive the third

• Definition of G**:* G = H - TS
• Differential:* dG = dH - d(TS) = dH - TdS - SdT
• Sub in dH from 2nd eq*

dG = TdS + Vdp - TdS - SdT

dG = Vdp - SdT

Question 10

Why is the 3rd master eq so useful?

dG = Vdp - SdT

Answer 10

change in pressure and temp can be used directly to calculate Gibbs energy

Question 11

Give the expression for how molar Gibbs energy varies with pressure, at constant temp, for an ideal gas.

Answer 11

G_m(p) = G^o_m + RT ln(p/p^o) (const. temp, ideal gas)

Question 12

Derive this expression for how molar Gibbs energy varies with pressure, at constant temp, for an ideal gas.

G_m(p) = G^o_m + RT ln(p/p^o) (const. temp, ideal gas)

Answer 12

• Third master eq:* dG = Vdp - SdT
• At constant temp, dT = 0, so*

dG = Vdp (const temp)

V varies with pressure p according to ideal gas eq:

pV = nRT, so V = nRT/p

Sub into eq for dG

dG = (nRT/p) dp

Then integrate from p₁ to p₂ (image)

So G(p₂) = G(p₁) + nRTln(p₂/p₁)

Take p₁ to be the standard pressure, p^o = 1 bar, then G^o = Gibbs energy at standard pressure

So G(p) = G(p^o) + nRTln(p/p^o)

divide through by n to make into molar quantities

G_m(p) = G^o_m + RT ln(p/p^o)

Question 13

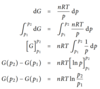
Give the expression for how Gibbs energy varies with volume, at constant temp, for an ideal gas.

Answer 13

G(V₂) = G(V₁) + nRTln(V1/V2) (const. temp, ideal gas)

Question 14

Derive this expression for how Gibbs energy varies with volume, at constant temp, for an ideal gas.

G(V₂) = G(V₁) + nRTln(V1/V2) (const. temp, ideal gas)

Answer 14

• Third master eq:* dG = Vdp - SdT
• At constant temp, dT = 0, so*

dG = Vdp (const temp)

V varies with pressure p according to ideal gas eq:

pV = nRT, so V = nRT/p

Sub into eq for dG

dG = (nRT/p) dp

Then integrate from p₁ to p₂ (image)

So G(p₂) = G(p₁) + nRTln(p₂/p₁)

For an ideal gas, pressure is inversely proportional to volume at constant temp, so p2/p1 = v1/v2:

So G(V₂) = G(V₁) + nRTln(V1/V2)

Question 15

Give the expression for how molar Gibbs energy varies with temperature, at constant pressure, for an ideal gas.

Answer 15

Gibbs-Helmholtz equation:

d/dT(G/T) = -H/T² (const. pressure)

Question 16

Derive this expression for how molar Gibbs energy varies with temperature, at constant pressure, for an ideal gas.

Gibbs-Helmholtz equation:

d/dT(G/T) = -H/T² (const. pressure)

Answer 16

Find an expression for dG/dT

• Third master eq:* dG = Vdp - SdT
• At constant pressure, dp = 0, so:*

dG = -SdT (const. pressure)

dG/dT = -S (const. pressure)

Then form an equation to sub the above into

Derivative of G/T wrt T, product rule:

d/dT(G/T) = T^-1(dG/dT) - T^-2(G)

Do the sub

d/dT(G/T) = T^-1(-S) - T^-2(G)

Sub in definition of G, G = H - TS

d/dT(G/T) = T^-1(-S) - T^-2(H - TS)

d/dT(G/T) = -T^-1(S) - T^-2(H) + T^-1S

d/dT(G/T) = -T^-1(S) - T^-2(H) + T^-1S

d/dT(G/T) = -T^-2H

d/dT(G/T) = -H/T² (const. pressure)

Question 17

When considering the Gibbs energies of mixtures (as necessary for discussing equilibrium), and for an ideal gas, what does the Gibbs energy of each gaseous species depend on?

Answer 17

Its own partial pressure, since by definition molecules in ideal gases don’t interact.

Question 18

Give the definitions (verbal and eq) of partial pressure and mole fraction of gas i within a mixture.

Answer 18

Partial pressure, p_i, in a mixture of ideal gases, is the pressure that substance i would exert if it occupied the whole volume alone.

p_i = x_ip_tot

where p_tot = total pressure and x_i = mole fraction of gas i

Mole fraction, x_i, is the moles of i as a fraction of the total moles of all species.

x_i = n_i/n_tot

where n_i = moles of i and n_i = total moles of all gases

Question 19

Give the expression for how molar Gibbs energy varies with pressure, at constant temp, for an ideal gas in a mixture. Explain where it comes from.

Answer 19

Recall G_m(p) = G^o_m + RT ln(p/p^o) (const. temp, ideal gas)

Ideal gases don’t interact, so there is no distinction between a pure gas at pressure p, and that same gas at partial pressure p_i in a mixture:

G_m,i(p_i) = G^o_m,i + RT ln(p_i/p^o) (const. temp, ideal gas)

where G_m,i(p_i) = molar gibbs energy of gas i present at partial pressure pi, etc etc

Question 20

Give the formula for the Gibbs energy of a mixture of ideal gases.

Answer 20

Ideal gases don’t interact, so just add the molar Gibbs energy of each species, each multiplied by its mole fraction, each at its own partial pressure:

G = n_AG_m,A(p_A) + n_BG_m,B(p_B​) + …

then you could replace each Gibbs energy with the formula in the prev fc

Question 21

Discussing the Gibbs energy of a mixture of ideal gases doesn’t apply to equilibria involving solutions, liquids or solids. So chemical potential is introduced instead.

What symbol is used for the chemical potential of say species A?

Answer 21

μ_A

Question 22

Discussing the Gibbs energy of a mixture of ideal gases doesn’t apply to equilibria involving solutions, liquids or solids. So chemical potential is introduced instead.

What equation gives the Gibbs energy of a mixture, using chemical potentials?

Answer 22

G = n_Aμ_A + n_Bμ_B + …

Question 23

Give the expression for how chemical potential of gaseous species i varies with pressure, at constant temp, in a mixture.

Answer 23

μ(p_i) = μ^o_i + RT ln(p_i/p^o)

• Analagous to:*
• G_m,i(p_i) = G^o_m,i + RT ln(p_i/p^o) (const. temp, ideal gas)*

Question 24

Give the expression for how chemical potential of ideal, dissolved species i varies with pressure, at constant temp, in a mixture.

solutions are rarely ideal, but this course assumes they are

Answer 24

μ(c_i) = μ^o_i + RT ln(c_i/c^o)

where c^o = standard conc, 1 mol dm^-3

• Analagous to:*
• G_m,i(p_i) = G^o_m,i + RT ln(p_i/p^o) (const. temp, ideal gas)*

Question 25

Give the expression for the chemical potential of a solid or liquid species i.

Answer 25

μ_i = μ^o_i

Since solids/liquids are always in their standard state, i.e. the pure substance