Energetics & Equilibria 4: Equilibrium

Question 1

Write the expressions for the eq constant for the following reaction involving

• gases
• dissolved species
• solids and liquids

A + B ⇔ P + Q

Answer 1

solids: trick question, solid species don’t contribute to expression

Question 2

Why do solids and liquids in reactions not contribute a term to the eq constant expression?

Answer 2

Chemical potentials of solids/liquids = standard chemical potentials

I.e. µ = µ^o, so the term that solid A with coefficient v_A = (µ/µ^o)^v_A = 1. Therefore the contribution is to multiply the overall expression by 1 – no change.

Question 3

What is true of Gibbs energy at equilibrium?

Answer 3

∆rG = 0

Effectively, ∆rG is the slope of a graph of Gibbs energy against composition, composition being the ratio of products to reactants. See image

Question 4

Give the expression linking the standard Gibbs energy of reaction and the equilibrium constant.

Answer 4

∆rG^o = -RTlnK

Question 5

Derive that ∆_rG^o = -RTlnK

Answer 5

Assume generic reaction A + B ⇔ P + Q

For a mixture of gases (NB you could do equiv calculation assuming solutions instead):

∆_rG = v_pμ_p(p_P) + v_Qμ_Q(p_Q) - v_Aμ_A(p_A) - v_Bμ_B(p_B)

Assume all species are gaseous

μ(p_i) = μ^o_i + RT ln(p_i/p_o)

Then sub in chemical potential expressions

∆_rG = v_p(μ^o_P + RT ln(p_p/p_o)) + vQ(…) - v_A(…) - v_B(…)

Gather together the standard chemical potentials

∆_rG = (v_pμ^o_P + v_Qμ^o_Q - v_Aμ^o_A - v_Bμ^o_B) + v_pRT ln(p_p/p_o) + v_Q(…) - v_A(…) - v_B(…)

Quantity in bracket = ∆_rG^o. Put the stoichoimetric coefficients onto the ln terms

So ∆_rG = ∆_rG^o + RT ln(p_p/p_o)^v_p + …etc

Then gather the ln terms, from here on see image

Question 6

CaCO₃(s) ⇔ CaO(s) + CO₂(g)

Derive an expression for Δ_rG^o at equilibrium.

Answer 6

Δ_rG = µ(CO₂) + µ(CaO) - µ(CaCO₃)

For the solids, µ = µ^o. For CO₂ gas, write in terms of partial pressure, recalling µ_i(p_i) = µ^o_i + RTln(p_i/p^o)

Δ_rG = µ^o(CO₂) + µ^o(CaO) - µ^o(CaCO₃) + RTln(p_CO2/p^o)

Δ_rG = [µ^o(CO₂) + µ^o(CaO) - µ^o(CaCO₃)] + RTln(p_CO2/p^o)

Quantity in [] = Δ_rG^o

Δ_rG = Δ_rG^o + RTln(p_CO2/p^o)

At equilibrium, Δ_rG = 0, so:

Δ_rG^o = -RTln(p_CO2,eq/p^o)

This demonstrates that, although solids/liquids don’t contribute to the expression for the eq constant K, they do still contribute to Δ_rG^o, and so they affect the value of K indirectly

Question 7

• Rearrange the standard Gibbs energy equation to make K the subject
• Use this to explain how the sign of the standard Gibbs energy predicts the position of equilibrium

Answer 7

Question 8

reaction with +ve change in standard gibbs energy proceeds to some extent. overall, going from reactants to products is associated with a rise in gibbs energy, so this isn’t spontaneous and doesn’t occur. however, it’s not a straight line from reactants to products – it’s a curve which falls then rises. at the minimum of the curve is where gibbs energy is at a minimum. this is the eq composition.

Use this graph to demonstrate the basis of Le Chatelier’s principle, e.g. why the act of removing products (altering concentration) is counteracted.

Answer 8

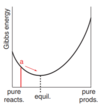
• removing product increases proportion of reactant in mixture
• graph moves from eq position to position marked a
• to return from a to eq is associated with a decrease in gibbs energy, therefore spontaneous
• so some reactants reform products to counteract the change

Question 9

• Derive the temperature-dependence of the equilibrium constant
• Use this to explain why, for an endothermic reaction, increasing temperature shifts eq to products, and vice versa

Answer 9

Derivation

Recall Δ_rG^o = -RTlnK and also Δ_rG^o = Δ_rH^o - TΔ_rS^o

So -RTlnK = Δ_rH^o - TΔ_rS^o

Divide through by -RT

lnK = -(Δ_rH^o/R)(1/T) + (Δ_rS^o/R)

Interpretation

Assume Δ_rH^o and Δ_rS^o are temperature-independent over a modest temperature range.

• For an endothermic reaction, Δ_rH^o > 0, so -(Δ_rH^o/R)(1/T) is negative, so increasing T makes the term less negative, so lnK and thus K increase. Shifts eq towards products (increased K)
• For an exothermic reaction, Δ_rH^o rH^o/R)(1/T) is positive, so increasing T makes the term less positive, so lnK and thus K decrease. Shifts eq towards reactants (decreased K)

NB this approach is only applicable for reactions which go to completion

Question 10

Another method for determining the temperature-dependence of K uses the Gibbs-Helmholtz equation. Write it out

Answer 10

d/dT(G/T) = -H/T² (constant pressure)

Question 11

Another method for determining the temperature-dependence of K uses the Gibbs-Helmholtz equation:

d/dT(G/T) = -H/T² (constant pressure)

Use this to derive the van’t Hoff equation:

dlnK/dT = Δ_rH^o/RT²

Answer 11

d/dT(G/T) = -H/T² (constant pressure)

Replace with standard quantities

d/dT(Δ_rG^o/T) = -Δ_rH^o/T² (constant pressure)

Sub in Δ_rG^o = -RTlnK –> Δ_rG^o/T = -RlnK

d/dT(-RlnK) = -Δ_rH^o/T²

Divide through by -R

dlnK/dT = Δ_rH^o/RT²

Question 12

Another method for determining the temperature-dependence of K uses the Gibbs-Helmholtz equation to derive the van’t Hoff equation:

dlnK/dT = Δ_rH^o/RT²

Use this to derive the temperature-dependence (should get the same result as before).

Answer 12

Question 13

For dissolved species, altering pressure doesn’t have a significant effect, but it does for gaseous species.

State how pressure affects the equilibrium constant and composition.

Answer 13

• For a gas phase reaction, K_p and ∆rG^o are related via ∆rG^o = −RT lnK_p, and ∆rG^o is defned under standard conditions (pressure = 1 bar), so K_p does not vary with pressure
• Composition of eq mixture changes in order to keep K_p constant

Question 14

Consider the following equilibrium:

A₂(g) ⇔ 2A(g)

Use the concept of the degree of dissociation to determine the pressure-dependence of the equilibrium composition.

Answer 14

Let α = degree of dissociation of dimer A₂, i.e. the fraction which have dissociated, where α = 0 means no dissociation and α = 1 means full dissociation.

n₀ moles of A₂ are allowed to reach eq at pressure p_tot, giving degree of dissociation α.

So n_eq,A2 = (1-α)n_o, and n_eq,A = 2αn_o, and therefore n_eq,total = (1+α)n₀.

Partial pressure of a species i: p_i = x_ip_tot

Then write out the partial pressures of each species and derive the eq constant, then rearrange for α (image from here on).

Question 15

How do biological systems drive thermodynamically unfavourable reactions?

Answer 15

• Couple an unfavourable reaction (Δ_rG^o > 0) to a favourable one (Δ_rG^o​ > 0) such that overall (Δ_rG^o​ > 0), so the reaction can occur
• Coupling occurs physically through connecting reactions closely, eg via an enzyme
• Examples:
  
  • ATP hydrolysis is often the favourable reaction used to drive another, e.g. protein synthesis
  • ATP synthesis is therefore unfavourable; it is coupled to glucose oxidation
  • Photosynthetic production of glucose is not favourable, so is coupled to light energy