Energetics & Equilibria 5: Electrochemistry

Question 1

Cell conventions:

• Each half cell is written as a reduction
• Both half cells involve the same #electrons, so conventional cell reaction (NB not necessarily spontaneous) = RHS half-reaction - LHS half-reaction

How is the cell potential calculated from the half-cells?

Answer 1

E_cell = RHS half-cell potential - LHS half-cell potential

Question 2

Describe the conventional shorthand notation for cells.

Answer 2

, indicates species in the same solution in the same phase

|| (or | x |) indicates a liquid junction (junction between solutions)

indicates species in the same solution in different phases

Question 3

For the following reaction, write

• the half-cells
• the shorthand notation for the cell

Cu²⁺(aq) + Zn(m) –> Cu(m) + Zn²⁺(aq)

Answer 3

Conventional cell reaction = RHS - LHS, so:

LHS: Cu²⁺(aq) + 2e^- –> Cu(m)

RHS: Zn²⁺(aq) + 2e^- –> Zn(m)

Cu(m) | Cu²⁺(aq) || Zn²⁺(aq) | Zn(m)

One | indicates different phases, and || indicates a liquid junction (junction between solutions)

Question 4

Write the conventional cell reaction for the following cell:

Pt(m) | H₂(g) | H⁺(aq) || Cd²⁺(aq) | Cd(m)

Answer 4

Question 5

Give the equation relating cell potential (of the conventional cell reaction) to Gibbs energy.

Cell potential is emf. NB proof for this equation is not required.

Answer 5

Δ_rG_cell = -nFE (constant temp and pressure)

Where F = Faraday constant, i.e. the charge on one mole of fundamental charges, and n = #electrons involved in cell reaction

I.e. in cells, emf is related to change in gibbs energy - allowing direct measurement. of gibbs energy

Question 6

Derive an expression for the entropy change of a cell reaction.

Answer 6

Recall 3rd master equation dG = Vdp - SdT

So dG = -SdT (constant pressure)

S = -dG/dT (constant pressure)

S = -(∂G/∂T)_p

Apply this to a cell:

Δ_rS = -(∂Δ_rG_cell/∂T)_p

Δ_rG_cell = -nFE

Δ_rS = -(∂(-nFE)/∂T)_p

= nF(∂E)/∂T)_p

I.e. practically, measure cell potential E over a range of temperatures, then plot E against T, and the entropy change is the slope.

Question 7

How is the enthalpy change of a cell calculated?

Answer 7

Rearrange Δ_rG_cell = Δ_rH_cell - TΔ_rS_cell

Find Δ_rG_cell using Δ_rG_cell = -nFE

Find Δ_rS_cell using Δ_rS_cell = nF(∂E)/∂T)_p

So Δ_rH_cell = TnF(∂E)/∂T)_p - nFE

Question 8

Write the expressions for:

• The chemical potential of a gas
• The chemical potential of an ideal solution
• (Recall for solids/liquids chemical potential = standard chemical potential)

Answer 8

Gas: µ_i(p_i) = µ_i^o + RTln(p_i/p^o)

Ideal solution: µ_i(c_i) = µ_i^o + RTln(c_i/c^o)

Question 9

For an ideal solution, µ_i(c_i) = µ_i^o + RTln(c_i/c^o)

However, solutions of ions are rarely ideal, so chemical potential must instead be written in terms of a different quantity. Write this expression.

Answer 9

activity, a_i:

µ_i(a_i) = µ_i^o + RTln(a_i)

Where, as c_i –> 0, a_i = (c_i/c^o)

i.e. solution becomes ideal in the limit of low concentration

Question 10

Write the Nernst equation for the generic reaction of solutions:

V_AA + V_BB –> V_PP + V_QQ

Answer 10

E = E^o - (RT/nF)ln( ((a_p)^Vp(a_Q)^VQ) / (a_A)^VA(a_B)^VB) )

Generally, E = E^o - (RT/nF) ln(products/reactants)

Question 11

Derive the Nernst equation for the generic reaction of solutions:

V_AA + V_BB –> V_PP + V_QQ

Answer 11

Δ_rG = V_pµ_P + V_Qµ_q - V_Aµ_A - V_Bµ_B

Recall, for non-ideal species i, µ_i(a_i) = µ^o_i + RTln(a_i)

• Sub in expressions for each activity in above equation
• gather up the V_iµ_i terms into square brackets, note they = Δ_rG^o, so replace them with this
• Gather the ln terms, raising the stoichiometric coefficients

Then follow image

E = E^o - (RT/nF)ln( ((a_p)^Vp(a_Q)^VQ) / (a_A)^VA(a_B)^VB) )

Question 12

Consider the reaction V_AA + V_BB –> V_PP + V_QQ

When the species are all solutions, the Nernst equation is:

E = E^o - (RT/nF)ln( ((a_p)^Vp(a_Q)^VQ) / (a_A)^VA(a_B)^VB) )

What is the equation when all species are gases?

Answer 12

E = E^o - (RT/nF)ln( ((p_P/p^o)^Vp(p_Q/p^o)^VQ) / (p_A/p^o)^VA(p_B/p^o)^VB) )

Replace activities with (partial pressure/standard pressure)

Question 13

Consider the reaction V_AA + V_BB –> V_PP + V_QQ

When the species are all solutions, the Nernst equation is:

E = E^o - (RT/nF)ln( ((a_p)^Vp(a_Q)^VQ) / (a_A)^VA(a_B)^VB) )

What is the equation when all species are solids/liquids?

Answer 13

E = E^o - (RT/nF)ln(1)

So E = E^o

Recall chemical potential = standard chemical potential

Question 14

• Give the generic form of the Nernst equation for half-cells
• Give the equation linking standard half-cell potentials to the standard cell potential

Answer 14

E_1/2 = E^o_1/2 - (RT/nF) ln(products/reactants)

E^o = E^o_1/2(RHS) - E^o_1/2(LHS)

Question 15

Define the standard half-cell potential of an electrode.

Answer 15

The potential of a cell in which the left-hand electrode is the standard hydrogen electrode, and the right-hand one is the one under test, and all species are present at activity = 1.

Question 16

For the standard hydrogen electrode:

• Write the conventional notation for this cell
• Write the half-cell reaction
• Describe the organisation of the cell

Answer 16

Pt(m) | H₂(g, p = 1 bar) | H⁺(aq, a = 1)

H⁺(aq) + e^- –> 1/2H₂(g)

H₂(g) at p = 1 bar in contact with H⁺(aq) at activity = 1, where an inert Pt electrode makes the electrical contact.

Question 17

The spontaneous cell reaction isn’t necessarily the conventional one, rather it’s the one which would occur if current were to flow.

State how the sign of the cell potential indicates whether the conventional cell reaction is spontaneous.

Answer 17

If cell potential E is positive, Δ_rG_cell is negative, since Δ_rG_cell = -nFE. So the direction of the conventional cell reaction is spontaneous.

If cell potential E is negative, Δ_rG_cell is positive, since Δ_rG_cell = -nFE. So the opposite direction of the conventional cell reaction is spontaneous.

Question 18

How could you make a non-spontaneous conventional cell reaction spontaneous?

Answer 18

Alter the concentrations of ions, since cell potential E is concentration-dependent according to the Nernst equation.

Question 19

The following is a metal/metal ion half-cell: a metal in contact with a solution of its ions. Write the Nerst equation for it.

Ag⁺(aq) + e^- –> Ag(m)

Answer 19

E = E^o(Ag⁺, Ag) - (RT/F) ln(1/a_Ag+)

note n = 1 here so RT/nF = RT/F

Question 20

Describe gas/ion half-cells

Answer 20

A gas in contact with a solution of related ions, where an inert Pt electrode provides the electrical contact

e.g. chlorine gas forms Cl^-

Question 21

A gas/ion half-cell involves H₂(g) and OH^-(aq). Write the conventional cell reaction and the Nernst equation.

Answer 21

Question 22

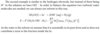
Describe redox half-cells.

Answer 22

Oxidised and reduced species are present in solution, where an inert Pt electrode provides electrical contact

E.g. Fe2+/Fe3+

Question 23

Describe metal/insoluble salt/anion half-cells.

Answer 23

An anion is in solution, and a metal is coated with a layer of the insoluble salt formed by the metal and anion.

Example image

Question 24

When the solutions in the two half-cells are different, they must be in contact without mixing.

• A liquid junction provides a porous barrier, allowing contact without rapid mixing. What is the issue with this?
• How do salt bridges avert this issue?

Answer 24

• A liquid junction potential may establish, which detracts from the cell potential, making the measurement inaccurate
• Salt bridges provide electrical contact whilst minimising liquid junction potential: tube typically containing conc KCl or KNO₃, sealed by glass sinters at each end, which dips into both solutions

Question 25

The electrochemical series is constructed using cell potentials.

Imagine a cell, where both half-cells consist of oxidised and reduced species, RHS A_ox/A_red and LHS B_ox/B_red.

How is the cell potential used to determine which oxidised species will oxidised which reduced species?

Answer 25

Conventional cell reaction: n_BA_ox + n_AB_red –> n_BA_red + n_ABox

If Δ_rG_cell is negative, the cell potential E is positive (indicating half-cell potential of A is more +ve than that of B), since Δ_rG_cell​ = -nFE, so the conventional cell reaction is spontaneous. So A_ox oxidises B_red.

Vice versa if Δ_rG_cell is positive.

In summary: a species with a more positive half-cell potential is more strongly oxidising.

Question 26

A species with a more __ half-cell potential is more strongly oxidising.

A species with a more __ half-cell potential is more strongly reducing.

Answer 26

A species with a more positive half-cell potential is more strongly oxidising.

A species with a more negative half-cell potential is more strongly reducing.

Since Δ_rG_cell = -nFE –> E = -Δ_rG_cell/nF, i.e. comparison of cell potentials is effectively comparison of Gibbs energy changes, corrected for #electrons involved – so don’t need to account for #electrons involved in redox couples

Question 27

When comparing redox couples whose standard half-cell potentials are not extremely similar, why is the fact that the concentrations of the species may not be the standard concentrations not significant?

Answer 27

Concentrations are within a ln term in the Nernst equation, so changing concentrations by a certain factor alters the cell potential by a smaller factor.

Question 28

AgI is a sparingly soluble salt, with solubility product K_sp, defined as the equilibrium constant for the following reaction:

AgI(s) ⇔ Ag⁺(aq) + I^-(aq) K_sp = (a_Ag+)(a_I-)

Calculate the concentration of the ions in solution, given the following information. State any assumptions made.

• F = 96,485 C mol^-1
• AgI(s) + e^- –> Ag(m) + I^-(aq), E^o = -0.15 V, at 298 K (1)
• Ag⁺(aq) + e^- –> Ag(m), E^o = +0.80 V, at 298 K (2)

Answer 28

Find Δ_rG^o for the reaction:

Subtracting (2) from (1) gives the conventional cell reaction, so subtracting the half-cell potential of (2) from that of (1) gives the standard cell potential

E^o = (-0.15) - (+0.80) = -0.95 V

Δ_rG^o = -nFE = -1 x 96,485 x -0.95 = +91.7 kJ mol^-1 = 91,700 J mol^-1

Then use the other eq for standard Gibbs energy to find K, i.e. K_sp

Δ_rG^o = -RTlnK –> K_sp = exp(-Δ_rG^o/RT)

= exp(-91,700/(8.3145 x 298) = 8.6 x 10^-17

Assume activities can be approximated by concentrations, so:

K_sp = ([Ag⁺]/c^o)([I^-]/c^o)

Standard conc = 1 molar, so:

K_sp = [Ag⁺]² = [I^-]²

[Ag⁺] = [I^-] = K_sp^1/2 = (8.6 x 10^-17)^1/2 = 9.3 x 10^-9 mol dm^-3

Sense-check: solubility of ions is a low value, as expected

Question 29

The enthalpies and Gibbs energies of formation of ions in solution can be determined by reference to the standard hydrogen half-cell. What are the conventional values for the latter?

Answer 29

Δ_fH^o(H⁺) = 0

Δ_fG^o(H⁺) = 0

Question 30

The enthalpies and Gibbs energies of formation of ions in solution can be determined by reference to the standard hydrogen half-cell.

Using the following information, calculate the standard Gibbs energy of formation of Ag⁺(aq).

• F = 96,485 C mol^-1
• H⁺(aq) + e^- –> 1/2H₂(g), E^o = 0 V, by definition (1)
• Ag⁺(aq) + e^- –> Ag(m), E^o = +0.80 V

Answer 30

Find ΔrG^o for the reaction:

• Subtracting (2) from (1) gives the conventional cell reaction*
  (1) - (2) = H⁺(aq) + Ag(m) –> 1/2H₂(g) + Ag⁺(aq)
• And subtracting the half-cell potential of (2) from that of (1) gives the standard cell potential*

E^o = (0) - (+0.80) = -0.80 V

ΔrG^o = -nFE = -1 x 96.485 x -0.8 = +77.2 kJ mol^-1

Write ΔrG^o in terms of standard Gibbs energies of formation, in order to obtain that of Ag⁺

ΔrG^o = 1/2 Δ_fG^o(H₂(g)) + Δ_fG^o​(Ag⁺(aq)) - Δ_fG^o​(Ag(m)) - Δ_fG^o​(H⁺(aq))

By convention, Δ_fG^o​(H⁺(aq)) = 0, and Δ_fG^o​ of elements in their reference states (here, H₂ and Ag) = 0, so:

ΔrG^o = Δ_fG^o​(Ag⁺(aq))

So Δ_fG^o​(Ag⁺(aq)) = +77.2 kJ mol^-1

Entropy change could be found using temp coefficient of cell potential, then enthalpy change could be found using entropy and Gibbs energy changes.

Question 31

A concentration cell has the same electrode on the LHS and RHS, but the species involved are at different concentrations or pressures. The cell potential thus depends on the ratio of concentrations in the two half-cells.

Consider the following cell, in which the activities of Cl^- are different on the RHS and LHS.

• Write the conventional cell reaction
• Write the Nernst equation
• State the condition required for the conventional cell reaction to be spontaneous
• Find expressions for ∆_rG_cell, ∆_rS_cell and ∆_rH_cell, stating any assumptions made

Ag(m), AgCl(s) | Cl^-(aq, a = a_L) || Cl^-(aq, a = a_R) | AgCl(s), Ag(m)

Answer 31

Conventional cell reaction

RHS: AgCl + e^- –> Ag + Cl^-(a_R​)

LHS: AgCl + e^- –> Ag + Cl^-(a_L​)

Conventional cell reaction = RHS - LHS:

Cl^-(a_L) –> Cl^-(a_R)

Nernst equation

E = E^o - (RT/F) ln(a_R/a_L)

The electrodes are the same, so E^o(RHS) = E^o(LHS), so E^o_cell = 0

E = -(RT/F) ln(a_R/a_L)

E = (RT/F) ln(a_L/a_R​)

Condition for spontaneity

If a_l > a_R, (a_L/a_R) > 1, so ln(a_L/a_R) > 0, so E > 0. So ∆_rG_cell is negative, since ∆_rG_cell​ = -nFE, so the spontaneous cell reaction is the same as the conventional cell reaction.

Makes sense as the chloride in the more concentrated solution is moving to that in the less concentrated solution

∆_rG_cell

∆_rG_cell = -nFE = -1 x F x (RT/F) ln(a_L/a_R​)

∆_rG_cell = RT ln(a_L/a_R​)

∆_rS_cell

∆_rS_cell = -(∂∆_rG_cell/∂T)_p

= -(RT ln(a_L/a_R​)/∂T)_p = (RT ln(a_R/a_L​)/∂T)_p​

= -Rln(a_R/a_L​)

∆_rH_cell

∆_rG_cell = ∆_rH_cell + T∆_rS_cell

So ∆_rH_cell = ∆_rG_cell - T∆_rS_cell

= RT ln(a_L/a_R​) - T(-Rln(a_R/a_L​))

= 0

As expected, since the half-reactions are the same.