(4.1,4.2) Teilraum und Quotiententopologie Flashcards
Definiere die Teilraumtopologie!

Beschreibe, wie die Basis eines topologischen Teilraums aussieht, wenn die Basis des Oberraums gegeben ist!



Erläutere die universelle Eigenschaft der Teilraumtopologie! Was gilt bezüglich Gröbheit/Feinheit?



Bei gegebenen Funktion f:X \rightarrow Y bespreche wann man f ⁓-invariant nennt und welche Abbildung das induziert. Wie macht man diese Abbildung injektiv? (Hinweis: ⁓f) Erläutere den Zusammenhang anhand eines kommutativen Diagrams!

Erläutere, wie man schrittweise die Quotiententopologie konstruiert!
Ich muss den Teil vor der Definition entfernen, weil ich ihn in der vorherigen Karteikarte schon habe. Ich konnte die Karte nicht editieren, weil Top auf der Festplatte gespeichert ist.

Gib ein Kriterium für die Abgeschlossenheit einer Teilmenge eines Quotientenraums!
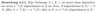


Erläutere die universelle Eigenschaft der Quotiententopologie ! Was gilt bezüglich Gröbheit/Feinheit?





