2 Topologische Räume

Question 1

Was versteht man unter einer Topologie? Was unter einem topologischen Raum?

Answer 1

Question 2

Was versteht man unter einem metrisierbaren Raum?

Wann nennt man zwei Metriken äquivalent? Nenne zwei konkrete Beispiele

Was versteht man unter einer Cofiniten Topologie?

Was versteht man unter der Sierpinski Topologie?

Ist der Schnitt von topologien wieder eine Topologie?

Answer 2

Question 3

Definiere:

1. die von S erzeugte Topologie von X
2. Subbasis S einer Topologie O

Answer 3

Question 4

Answer 4

Question 5

Definiere folgende Begriffe: Basis B einer Topologie; die von B erzeugte Topologie!

Answer 5

Question 6

Answer 6

Question 7

Answer 7

Question 8

Question 9

Question 10

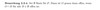
Wann nennt man eine Topologie (echt) feiner als eine andere Topologie?

Wann nennt man eine Topologie (echt) gröber als eine andere Topologie?

Answer 10

Question 11

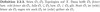
Bespreche den Begriff der Abgeschlossenheit!

Answer 11

Question 12

Answer 12

Question 13

Definiere folgende Begriffe:

• Umgebung
• Umgebungssystem
• Umgebungsbasis
  *

Answer 13

Question 14

Answer 14

Question 15

Answer 15

Question 16

Definiere für eine Teilmenge eines topologischen Raums

• Abschluss und Berührungspunkte
• Innere und innere Punkte
• Rand
• Ableitung und Häufungspunkte

Answer 16

Question 17

Answer 17

Question 18

Wann nennt man eine Teilmenge eines top Raums dicht, und wann nirgends dicht?

Answer 18