Z-scores, Outliers, CIs & Normal Distributions

Question 1

Properties of a normal distribution

Answer 1

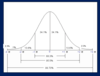
1. The majority of scores lie around the centre
2. The mean, median and mode will fall on the mid-point
3. The curve is symmetrical around the centre
4. Area under curve is directionally proportional to the relative frequency of observations
5. The majority of scores (approx two thirds) fall within 1 SD either side of the mean

Question 2

Normal distribution and standard deviation

Answer 2

Question 3

z-scores

Answer 3

• z-scores are standardised scores with a mean of 0 and a SD of 1
• A z-score is just the number of SDs a score is above or below the mean

Question 4

Using z-scores to detect outliers

Answer 4

• 99.9% of a sample will have z-scores between -3.29 and +3.29.
  
  • Any z-score below -3.29 and above +3.29 must be an extreme outlier.

Question 5

Dealing with outliers

Answer 5

1. Remove
2. Transormation

Do it BEFORE we test for normal distribution

Question 6

Assumptions of parametric tests

Answer 6

• Interval data
• Independent scores
• Normally distributed data

Question 7

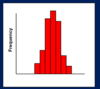
Leptokurtosis

Answer 7

Very pointed/short tails

Question 8

Platykurtosis

Answer 8

Very flat/long tails

Question 9

Mesokurtosis

Answer 9

Normal kurtosis

Question 10

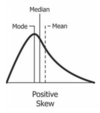
Positive skew

Answer 10

Tail on the right side of the distribution is longer or fatter.

Question 11

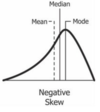
Negative skew

Answer 11

The tail of the left side of the distribution is longer or fatter than the tail on the right side

Question 12

Using z-scores to assess normality

Answer 12

• Calculate z-score for skewness and kurtosis
  
  • z(skewness)= skewness/SE(skewness)
  • z(kurtosis) = kurtosis/SE(kurtosis)
• Small samples (N<100): z-scores below -1.96 or above +1.96 are significant → skew or kurtosis
• Medium samples (N>100): z-scores below -3.29 or above +3.29 are significant → skew or kurtosis
• Large samples (N>300): don’t look at z-score of skewness or kurtosis
  
  • Look at histogram
  • Look at actual raw skew/kurtosis value in table
  • Value >2 indicates non-normality

Question 13

Kolmogorov-Smirnov test

Answer 13

• Tests for normal distribution
  
  • If significantly different (p<.05), then non-normally distributed
  • If non-significant (p>.05), then normally distributed
• K-S test is very sensitive to number of participants therefore not recommended

⇒ Use z-score or histogram to determine normal distribution

Question 14

Confidence interval (95% CI)

Answer 14

• The range within which the true mean is likely to be in 95% of instances
• Assume population is normally distributed → Then 95% of scores fall between -1.96 and +1.96 SDs either side of the mean.