Correlations

Question 1

Correlation

Answer 1

• Examines the relationship between two variables
  
  • Whether they are are associated with each other
  • How they are associated with each other
• Cross-sectional design: two measures are taken from each person at a specific time point

Question 2

Regression line

Answer 2

• Linear regression is a way to fit the best line (model) to the data
  
  • Regression line = line of best fit

Question 3

Positive relationship

Answer 3

As scores one variable increase, scores on another variable increase

Question 4

Negative relationship

Answer 4

As one increases the other decreases

Question 5

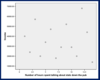
No relationship

Answer 5

No correlation - data points scattered irregularly

Question 6

Perfect correlation

Answer 6

All of the data points lie on the line

Question 7

Correlation coefficient

Answer 7

• Determines the strength and direction of the relationship by calculating the correlation coefficients
  
  • Direction:
    
    • • → positive correlation
    • • → negative correlation
  • Strength: look at value - indicated by a number from -1 to +1
    
    • -1 → perfect negative correlation
    • +1 → perfect positive correlation
    • 0 → no correlation
    • r = .10 = small/weak
    • r = 0.30 = medium/moderate
    • r = .50 = large/strong
• Two types:
  
  • Pearson’s r: for data that meet assumptions of normality
  • Spearman’s rho (r_s): for data that violate assumptions of normality

Question 8

Pearson’s r assumptions

Answer 8

• Parametric test:
  
  • Interval or ratio data
  • Normally distributed data
• Linear:
  
  • Assumes any underlying relationship is linear

Question 9

Pearson’s r formula

Answer 9

Ration of how much scores vary ‘together’ compared to how much they vary overall

Question 10

Pearson’s r SPSS output

Answer 10

Question 11

Effect size for Pearson’s r

Answer 11

• r is itself a measure of effect size - we don’t need anything else
• Cohen’s recommendations:
  
  • r = .10 = small/weak
  • r = 0.30 = medium/moderate
  • r = .50 = large/strong

Question 12

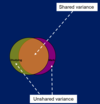
Shared variance R²

Answer 12

• If there is a relationship between two variables, then as scores on one change, scores on the other change
• Shared variance = R² (r x r)

Question 13

Spearman’s rho r_s

Answer 13

• When our data don’t meet assumptions for parametric tests e.g. ordinal data, skewed data
• First converts scores into ranks and then runs an analysis on the ranks
• Less influenced by single extreme cases
• R^<em>2</em> = proportion of variance in ranks that is shared → not useful

Question 14

Spearman’s rho r_s SPSS output

Answer 14

Question 15

Kendall’s tau

Answer 15

• Nonparametric test of correlation
• Ideal for small data sets with a large number of tied (same) ranks
• Can’t square it to get shared variance