Multiple Regression

Question 1

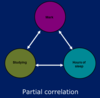
Partial correlation

Answer 1

Correlation between two variables while controlling for a third (a “first-order partial correlation”)

Question 2

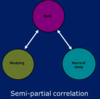
Semi-partial correlation

Answer 2

Relationship between two variables while accounting for the relationship between a third variable and one of those variables

Question 3

Multiple regression rationale

Answer 3

• Cross-sectional design - when we have measured more than 2 variables
• Increase predicted variance in outcome
• We can determine:
  
  • how well the model explains the outcome
  • how much variance in the outcome our model explains
  • the importance of each individual predictor

Question 4

Types of multiple regression

Answer 4

• Forced entry (enter) - all in at once
• Hierarchical - researcher decides order variables are entered in blocks
• Stepwise - SPSS decides the order they are entered

Question 5

Variance in multiple regression

Answer 5

• R us not particularly useful in multiple regression because we have several variables in the model
• R² : variance in the model accounted by all predictors
• Adjusted R²: adjusted for number of predictors in model
  
  • An indicator of how well our model generalises. The closer R² is to adjusted R² the more accurate our model is likely to be for other samples

Question 6

Multiple regression output in SPSS

Answer 6

Question 7

Regression coefficients in SPSS

Answer 7

Use unstandardised beta coefficients for multiple regression equation

Question 8

Assumptions for multiple regression

Answer 8

Pre-design:

• Outcome variable should be continuous
• Predictor variables should be continuous or dichotomous
• Should have reasonable theoretical ground for including variables

Post-data collection:

1. Linearity
2. Homoscedasticity/no heteroscedacity
3. Normal distribution of residuals
4. No multicollinearity
5. Influential cases

Question 9

Linearity

Answer 9

Relationship between each predictor and the outcome should be linear

Question 10

Homoscedasticity/ No heteroscedasticity

Answer 10

• Variance of error term (residuals) should be constant for all values of the predicted values (model)
• Look to see that data points are reasonably spread for all predicted values
• Look at a plot of standardised residuals by standardised predicted values
• Heteroscedasticity: when the variance in the error term is not constant for all predicted values - a funnel/cone shape may indicate heteroscedasticity

Question 11

Normal distribution of residuals

Answer 11

In regression it is important that the outcome residuals are normally distributed

Question 12

No multicollinearity

Answer 12

• Multicollinearity problems can occur when predictors correlate very strongly: predictors should not correlate too highly (e.g. r>.8 or .9)
• Problem:
  
  • A good predictor might be rejected because a second predictor won’t explain much more unique variance in the outcome than the first predictor
  • Leads to error in estimation of regression coefficients (the beta values)
• Possible solutions:
  
  • If it makes sense could try to combine predictors into one single variable
  • Might be necessary to remove one of the variables
• In SPSS: look at tolerance or VIF statistic (tolerance = 1/VIF)
  
  • VIF: worry if greater than 10
  • tolerance: less than 0.1 is cause for concern (0.2 may also be of concern)
  • High R² with non-significant beta coefficients might also be another indication

Question 13

Influential cases

Answer 13

• Individual cases (outliers) that overly influence the model
• Cook’s distance: checks for influential outlier cases in a set of predictors
  
  • Measures the influence of each case on the model
  • Values greater than 1 may be a cause of concern