One-way independent ANOVA

Question 1

Limitations of the t-test

Answer 1

Familywise error: each additional t-test increases the chance of making a type I error

Question 2

What is ANOVA?

Answer 2

• Used like the t-test: to compare 3 or more condition means
• Advantage over t-test: doesn’t increase chances of Type I error
• ANOVA hypothesis tested:
  
  • null hypothesis = means don’t differ
  • experimental hypothesis = the means differ
• ANOVA is an omnibus test: it tests for an overall difference between conditions - whether the means differ, but not which means differ

Question 3

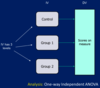
One-way independent ANOVA

Answer 3

• 3 or more group means (somes called ‘between-groups ANOVA’)
• One IV

Question 4

Systematic variation

Answer 4

Variation due to something the experimenter has manipulated

Question 5

Unsystematic variation

Answer 5

Variation that is the result of random factors between conditions

Question 6

Rationale of ANOVA

Answer 6

• ANOVA = Analysis of Variance
• Compares systematic to unsystematic variance i.e. how much of the variance is due to our manipulation vs how much is just random variation
  
  • Our manipulation has had an effect on our DV if it has created a lot of variation in scores compared to the random variation we’d find anyway
  • Our manipulation has not had an effect on our DV if there is not much variation in scores compared to random variation that we’d find anyway

Question 7

Independent ANOVA by hand

Answer 7

1. Calculate the within-group variance
   
   • Called within-group sum of squares: SS_W (or residual sum of squares SS_R)
2. Calculate the between-groups variance
   
   • Called between-group sum of squares: SS_B (or model sum of squares SS_M)
3. Effect of our manipulation = between-groups variance/ within-groups variance
   
   • Need to account for degrees of freedom (df):
     
     • For SS_W, df_w = sum of participants/scores in each group -1
     • For SS_B, dfB = k-1 (k = no of conditions/groups)
   • Use mean sum of squares (MS): divide the sum of squares by the df
   • Final F is MS_B/MS_{<span>W</span>} also expressed as MS_M/MS_{<span>R</span>}
   • The larger the F-value, the less likely that it occurred by chance
4. Use a table of “critical values of F” to check for significance

Question 8

Assumptions of Independent ANOVA

Answer 8

Parametric test:

• Normal distribution
• Data are measured at the interval/ratio level
• Homogeneity of variance

Question 9

ANOVA SPSS output

Answer 9

Question 10

ANOVA effect size

Answer 10

• Partial eta squared
• 0.01 = small
• 0.06 = medium
• 0.14 = large

Question 11

Independent ANOVA - if assumption of homogeneity of variance is violated

Answer 11

Welch statistic