Supervised Learning Flashcards
Model Evaluation Metrics - Which beta to use(high or low) - Fraud Detection
need a high recall, so need a high beta.
Model Evaluation Metrics - R2
comparing model MSE from basic model MSE. The idea is that the model MSE should be lower than basic model MSE. If so, the ratio is small and 1 - ratio is close to 1.
Ensemble Methods - Introducing Randomness to high variance models before ensembling. Two common options
Bootstrap the data - that is, sampling the data with a replacement and fitting your algorithm to the sampled data.
Subset the features - in each split of a decision tree an ensemble of only a subset of the total possible features are used.
Decision Tree - Entropy - How to turn a bunch of products into sums? To make the probability calculate more manageable.
Take the log of each item and sum everything together
Support Vector Machines - Which equation will help us split the data?
The function that splits the data will be x2 + y2 = 10 (10 being in the middle of 2 and 18)
Decision Trees - Entropy - Confirm how to calculate probabilities of recreating ball sequence
Since you grab the ball, and put it back each time, these are independent events and probabilities are multiplied by each other. *blue on first row should be zero
PyTorch - Batch Size?
Download and load the training data
trainset = datasets.MNIST(‘MNIST_data/’, download=True, train=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64, shuffle=True)
Each run through the network will use 64 images, then matrix where first column is a flattened vector version of one image
Ensemble Methods - Adaboost hyperparameters
base_estimator: The model utilized for the weak learners (Warning: Don’t forget to import the model that you decide to use for the weak learner).
n_estimators: The maximum number of weak learners used.
Bayes Theorem - Naive Bayes Fip Step. Use example below
Flip the event and conditional.
P(A | B) becomes P(B|A) * P(A). Think in terms of a diagram.
What is feature scaling, two common scalings?
transforming your data into a common range of values. There are two common scalings:
Standardizing
Normalizing
Allows faster converenge, training less sensitive to the scale of features
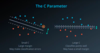
Support Vector Machines - Describe C Parameter
- C hyper-parameter determines how flexible we are willing to be with the points that fall on the wrong side of our dividing boundary
- Constant that attaches itself to classification error
- Large C = forcing your boundary to have fewer errors than when it is a small value. If too large, may not get converence with small error allotment
- Small C = Focus on large margin
Ensemble Methods - Explain Bias
When a model has high bias, this means that means it doesn’t do a good job of bending to the data. An example of an algorithm that usually has high bias is linear regression. Even with completely different datasets, we end up with the same line fit to the data. When models have high bias, this is bad.
Linear Regression - Describe the Square Trick
Its the absolute trick and some. Multiply the distance of the point from the line against the scaled slope and y-intercept. More smart as it gives the line a smarter distance to change to get closer to the point.
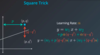
make a prediction, calculate the error, update weights and bias with gradient of error(scaled by learning rate)
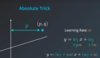
Linear Regression - Describe the absolute trick
Adding values to the slope and y intercept to make the line come closer to points. The value added to the slope should be the horizontal distance(p) and the value added to the y-intercept is arbitrary, but typically use 1. Then, must down scale these added values by a learning rate so the line doesn’t overshoot the point.
Support Vector Machines - Describe Margin Error
norm of the vector W squared. AKA, square all coefficients and sum. You want a small error as this indicates a larger margin.
Support Vector Machines - Describe the Kernel Trick
Transforming data from lower dimensions to higher dimensions in order to split with higher dimensional hyperplane. Then, project back to lower dimensional world with polynomial of certain degree.
Describe Lasso Regularization
Allows for feature selection
Formula squishes certain coefficients to zero, while non zero coefficients inidcate relevancy
use an alpha(lambda) multiplied by sum of the absolute value of each coefficient. Adds this to error
Ensemble Method - Boosting Simple Example
Instead of just taking most common answer, use answers from friends who are well versed in each question. Use answer from philospher friend for philosohy question, use answer from sports friend for sports question etc
Support Vector Machines - Define gamma in terms of sigma
If gamma is large, the sigma is small(curve is narrow). Vice Versa
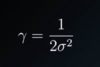
Ensemble Methods - Basic idea of Random Forest
Take Subset of data and build decision tree of these columns. Repeat process with other random subset, then use most popular prediction as the prediction
Model Evaluation Metrics - What is recall
Ensemble Methods - High level what are they and name two popular options
Take a bunch of models and join together to get a better model
Bagging(Bootstrap aggregating) and Boosting
Bayes Theorem - Naive Bayes - Normalize Step
Take conditional probabilities for all events(Spam and Ham), then normalize the values. (each probabilty over the sum of possible probabilities)
Preprocessing - What to do in this scenario
Subtle, but you only need two columns since there are only 3 possibilities. If you include all three, you are duplicating data and certain models may have trouble
Decision Trees - Describe Entropy
How much freedom do you have to move around
PyTorch - What does the transform function do?
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)),
])
first transform images to tensors,
then convert pixel values from 0-1 range to a -1 to 1 range
You are subtracting the mean(0.5) from each color channel(3), then dividing (0.5) from each color channel.
Ensures variance is zero centered which makes learning easier
Ensemble Methods - Bagging Simple example
Have all our friends take a true/false test and for each question use the most common answer
Describe Gradient Descent
Take the derivative of an error function and move in the negative direction. The negative direction gives us the fast way to decrease the error function
Support Vector Machines - Describe Margin and Classification Error
When linearly separating data, Margins maximize the distance from the linear boundary to the closest points (called the support vectors).
Incorrectly classifed points within the Margin is the Margin Error
Any errors outside the margin are considered classification errors.
Training and Tuning - K Fold Cross Validation Shuffle
Instead of equal splits, randomly creating different training and testing buckets K times
Model Evaluation Metrics - Quiz
Model Evaluation Metrics - ROC- What does score rerpresent
Area under ROC.
Support Vector Machines - Where would SVM make cuts?
two lines to maximize margin
Model Evaluation Metrics - F1 score
The harmonic mean of recall and precision
Will always be lower than arithmetic mean, so which ever score is lower, it will be closer to that, and thus raise a “red flag”
Support Vector Machines - Describe Classification Error
- Split data with line that represents Mx + b = 0,
- Add margin lines = Mx + b = -1, Mx + b = 1
- From Margin lines, create lines going up and down.
- Find incorrectly classified points inside and out margins,
- Associate a value based on point location, add all together
Ensemble Methods - Downside of Random Forests
They are random, there are better ways to choose which data to subset
Linear Regression - What variables can you change to move a line
Slope and Y intercept
Model Evaluation Metrics - Create an Accuracy Function
Support Vector Machines -What is it and name three popular versions?
popular algorithm used for classification problems
- Maximum Margin Classifier
- Classification with Inseparable Classes
- Kernel Methods
Model Evaluation Metrics - When Accuracy is not good
If your accuracy is high, but your not detecting errors. Can occur when data is skewed with high number of positive versus low number of errors
Bayes Theorem - Discuss Naive Bayes
Involves multiple events and assumes independence
For P(A & B), we assume events are independent. If they were depependent, they couldn’t occur together.
Think P(being HOT & Cold). This can’t happen, however, Naive says they can.
Just multiplying all events together, multiplying by the “given” and normalizing ratio.
Support Vector Machines - Gamma Parameter
Small = wide RBF, may underfit, may generalize better
Large = narrow RBF, may overfit. Similiar to Large C in classificaiton where it attempts to classify every point correctly
two categories of supervised learning
Training & Tuning - Describe Model Complexity Graph
One one end, your model underfits the data(high bias and doesn’t do well on either training or validation)
On other end, your model overfits(high variance, too complex, fits training data well but doesn’t generalize well
In middle, your model does pretty good on training and validation. Look for models where validation error is increasing but training error is reducing.
Decision Tree - Entropy - Simplified Entropy Equation
probabilty * log of probability
sum across and take negative value.
Ensemble Methods - Bagging Describe in more detailed
Take random cuts of data(weake learners), then superimpose over each other and vote(if two or more are red then red, two or more are blue, then blue)
Model will cut data according to votes
Visualize Mean Absolute Error
Model Evaluation Metrics - Purpose behind an ROC curve
provide a score that shows how well we split the data. 1 for perfect, .5 for random and above .5 for anything else
Ensemble Methods - Adaboost weighting
- weight all data points at 1
- minimize sum of weights of incorrectly classified points
- After first cut, calculate weight by taking natural log of correct/incorrect
- multiply incorrect weights by the weight
- Repeat
What type of gradient descent is used most often
Mini - Batching - Split data into mini batches of equal size, update weights based on each mini batch
Calculating error for ALL points(either by batch or one by one(stochastic) is slow
Training and Tuning - Learning Curves
Method of detecting if model is overfitting or underfitting. As more data points are used, training error increases and CV error descreases. Look at convergence point to determine if model is overfitting or underfitting
Bayes Theorem - High Level Description
Involves a Prior and Posterior Probability. Use new information to update prior, this becomes the posterior.
Decision Trees - Entropy described by probability
How much freedom do you have to move around or rearrange the balls
Ensemble Methods - Explain Variance
When a model has high variance, this means that it changes drastically to meet the needs of every point in our dataset. Linear models like the one above is low variance, but high bias.
A decision tree, as a high variance algorithm, will attempt to split every point into it’s own branch if possible. This is a trait of high variance, low bias algorithms - they are extremely flexible to fit exactly whatever data they see.
Ensemble Methods - Combining Weights
Superimpose all weak learner models
For each weak learner model, input the positive and negative weight value accordingly. Where sum for each region is positive, then classify positive, where negative, classify negative
Support Vector Machines - Where would SVM split and how?
Use kernel trick to move from 1-D line to 2-D(Plane) where points are placed on a parabola instead of a line. Find line that cuts the parabola cleanly, equate the line to the parabola and solve. These is where SVM makes cuts.
Support Vector Machines - RBF(Radial Basis Function)
- using functions to build mountains over each point
- record values in a vector of all mountains over each point.
- plug them into higher dimensional space
- find equation of hyperplane that splits data
- Take constants of the equation of the plane
- plug points at these constants and find line that splits dat (Where hyperplane intersects mountains)
Model Evaluation Metrics = What is precision of this model
Training and Tuning - K-Fold Cross Validation
Split data into Training and Testing K Times. Each pass the bucket of training and testing is different. Take average result for all runs
Support Vector Machines - Describe the degree of the polynomial kernel. Describe a degree 3 polynomial kernel
A hyperparameter we use during training to find best possible model
Support Vector Machines - What is a kernel? Describe different kernels
Set of functions that will come to help us out.
Linear Kernal - can only use x and y to create a line which separates data
Polynomial Kernel - Add, xy x2 and y2. Can create many more functions to separate data
RBF Kernel - Build mountains over each point
Decision Trees - Hyperparmaters - Describe Maximum Depth
largest length between the root to a leaf. A tree of maximum length kk can have at most 2k2k leaves.
Model Evaluation Metrics - Discuss Boundaries of Beta and impact on precision and recall
Log Transformation - Provide example
Model Evaluation Metrics - How is ROC calaculated
Calculate True Positive and False Positive Rates for all splits of data. Then plot
must drop the point values into the equation to determine q prime
Support Vector Machines - What does Sigma relate to in a normal distribution
The width of the mountain/curve
Model Evaluation Metrics - F-beta score
Used when you want your model to care more about either precision or recall.
Its a weight added to the F1 score to swing the value either way
3 main categories of machine learning
Decision Trees - Entropy - Once you have the sum of the negative logs, what is the next step
Take the average
Support Vector Machines - Margin Error - Describe W Vector
- Used in distance calculation between two lines
- Random vector that runs from orgin and intersects second line
- Based on intersection points(p,q) and the equation of the line the vector intersects (Wx = 1), the 1/|W| square represents the distance from Wx = 0 to Wx = 1. Multiply by 2 since lines are equidistant and 2/|W| squared represents the Margin Error.
Model Evaluation Metrics - Type 1 and 2 errors
Decision Trees - Hyperparameters - Describe minimum number of samples per leaf
Ensemble Methods - Weak versus Strong Learners
Weak learners = our friends who take test
Strong Learner = Genius who combins all answers
Two common error functions in linear regression
Mean Absolute Error - Make all errors positive so the negatives don’t cancel each other out.
Mean Squared Error - Take all errors and square them to make them non-negative. This gives you the area of a sqaure around each point. Sum and Average than multiply by 1/2 to facilitate taking derivative
Support Vector Machines - Describe the x2 + y2 = 10 in single and multiple dimensions
Model Evaluation Metrics - Precision
Accuracy of Diagnosed Positive Group
Model Evaluation Metrics - Recall
Accuracy of Positive Group
Decision Trees - Entropy describe by knowledge
Less entropy = less room to move around = more knowledge you have
Model Evaluation Metrics - Describe a confusion matrix
Rows = Positive versus negative
Columns = Guessed Positive, Guessed Negative
Decision Trees - Information Gain - How to calculate?
- Change in Entropy between part node and children node
- Parent Entropy is always 1
- Take weighted average of the children
Bayes Theorem - Known versus Inferred?
Known
You know a P(A) and you know P(R | A)
Inferred
Once we know the event R has occurred, we infer P(A | R)
Find conditional probability of event and divide into possible events that have occurred.
Since the point is below the line, the intercept decreases; since the point has a negative x-value, the slope increases.
If point was above line, then you would add the alpha and p*alpha
Explain Batch vs Stochastic Gradient Decent
Batch - Calculate error for all points, then update weights
Stochastic - calculate error for one point, then update weights
Bayes Theorem - Naive Bayes - Be Naive Step
Split into a product of simple factors. Then, multiply by Prob of Event
Do this for all possible events (Spam & Ham)
Vizualize Mean Squared Error
Decision Trees - Entropy - Formula - Describe the formal notation
- find prob of each event
- take negative log
- multiple by occurences of event
- Take average
- Repeat for each probability
- Sum
Support Vector Machines - Describe the photo below in relation to gamma
Large Gamma = trying to classify every point
Small Gamma = Clusters
