general Flashcards
Does the Random Contraction Algorithm always gives you the minium cut?
No this is a random algorithm. It will return the minimum cut solutions only on average!
What is the complexity of addition of 2 array of n-digits N+N?
It is O(n) or O(logN) where N is the actual value of the number. Indeed the number of digits n is n= is log10(N)
What is the fastest you can be in sorting an array (theoretical bound)?
Nlogn you can never ever get linear time in sorting! So you should love merge sort quick sort etc!
What is the complexity of a simple sorting algorithm? name a few of them
They are all n^2 like insertion bubble sort etc. Merge sort a recursive algorithm is actually a n*logn +n algorithm
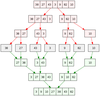
High-level description of a partition with linear time and no memory loss (in place)
See image below, go through the swapping in your mind
For an array n what is the maximum number of inversions?
eVERY COUPLE you peek would bein the wrong order with i>j so it is the number of paris (n 2) n(n-1)/2
What is the maximum and the minimum number of edges in a graph connected undirected with no parallel edges?
Minumum is n-1 maximum is n(n-1)/2
What is the worst case time for a random selection algorithm if the pivot is chosen poorly?
It is O(n^2) like for quicksort. The size of the array you re recursing on reduce as n, n-1, n-2 .. and every time you do a partition which is an O(n) algorithm
How does merge sort work?
Like QuickSort, Merge Sort is a Divide and Conquer algorithm. It divides input array in two halves, calls itself for the two halves and then merges the two sorted halves. The merge() function is used for merging two halves. The merge(arr, l, m, r) is key process that assumes that arr[l..m] and arr[m+1..r] are sorted and merges the two sorted sub-arrays into one. See following C implementation for details.
MergeSort(arr[], l, r)
If r > l
- Find the middle point to divide the array into two halves: middle m = (l+r)/2
- Call mergeSort for first half: Call mergeSort(arr, l, m)
- Call mergeSort for second half: Call mergeSort(arr, m+1, r)
- Merge the two halves sorted in step 2 and 3: Call merge(arr, l, m, r)
Karatsuba multiplication: simple way to see the formual and a bit of details
it is a n^log_2(3) n^1.6 algorithm compare to the simple quadratic one. Just write x= 10^n/2 a +b y= 10^n/2 c +d and go from there
What is the best case scenario (in the choice of the pivot) in random selection? what is its time?
As usual, you want to reduce the size of the problem. So best case scenario is in balance, split the array in equal sizes sooo… the median
if you do that then each iteration
T(n)<t></t>
<p>note now is T(n/2) not 2*T(n/2) like in quicksort. We only need to look at one sort of the subarray</p>
<p>from master method --><strong> linear time O(n)</strong></p>
</t>
Counting inversions: given array count how many object i,j with i>j not adjiacent!! Speed, use etc
with divide and conquer you can get to n*log(n) (as usual we want to have a almost linear algorithm) This is good for similarities say you rank movies and want to check how much 2 lists are close (zero inversion mean very close.)
High level description of quick sort?
Partition (around a pivot): what is the running time? what about memory
They are linear O(n) and need no memory needed just swap!
What is the complexity of merge sort?
n*logn +n
Quick sort worst and best case behaviour?
n^2 for the worst n logn for best case scenario but on average very close to best behaviours (decomposition principle)
How many different minimum cuts are there in a tree with n nodes (ie. n−1 edges)
Any edge is a minimum cut if you think about it cause every vertex is connected to the graph by one edge
so there are n - 1 minimum cuts.
What is the key of the so called decomposition principle for a randomized algorithm?
- Identify what is the random variable Y you are really interested in
- Express that as a sum of simpler (indicator i.e variables that takes the )
- Apply linearity of expectation E[sum(x)] = sum(E(x)) that works even for dependent variables.
What is the pivot element in quick sort?
It is an element of the array you pick such that all the elements to the left are smaller than the pivot while all the element on the right are bigger (note they are not ordered!)
Also, note the pivot ends up being in the right place (the finally place it will be in the array after sorting)
What is the best way to analyze a recursive algorithm?
Use a recursive tree, find the number of levels (depth) it is usually log(n) at each level j you have 2^j cases that operate on array of size n/2^j then you only have to know the complexity/time of level j (hopefully it is independent of the level)
What is O() of nested loops if for i to n; for j i+1 ..n ?
The same still O(n^2) you just save a factor of 2 or so
Can integers overflow in python?
Short answers: No if the operations are done in pure python, because python integers have arbitrary precision Yes if the operations are done in the pydata stack (numpy/pandas), because they use C-style fixed-precision integers
Results of master method!!
if the recursive time at one step T(n) is < aT(n/b) + O(n^d) i.e the recursive plus the merging step time. Now we have three cases
- 1) a=b^d time is n^d log n
- 3) ad we have O(n d)
- 2) a>b^d here how many recursion is crucial time is n^(log_b(a))
Minimum cut graph random contraction algorithm!
First, Random sampling very efficient for sorting and graph problem.
Pick a random edge uniformly. Fuse the 2 vertexes into one. You can create parallel loops (keep) or self loop(kill them).
Once you get the last 2 vertices that is the cut: the one represented by the vertices fused with 2 vertices.
What is the key to count inversion fast?
To also merge sort we want to sort and count!
How many times would 2 objects of an array be compared in the quicksort algorithm?
0 or 1 no more!
because when comparing one is the pivot. Then that number the pivot is removed from the future recursive call
What is O() of a loop?
O(size of the loop) it is a linear algorithm, like searching if a number is in an array
Outline the algorithm for randomized selection!
It is a reduction (reduce a problem to one you already know how to solve) of quick sort.
say you look for the j-th statistics
you partition with a pivot that ends up in ith position
if i=j you stop
if i>j you look at the left array for a j statistics
i<j>
</j>
What are some benefit of insertion sort?
Efficient for (quite) small data sets, much like other quadratic sorting algorithms
More efficient in practice than most other simple quadratic (i.e., O(n2)) algorithms such as selection sort or bubble sort
efficient for data sets that are already substantially sorted: the time complexity is O(kn) when each element in the input is no more than k places away from its sorted position
Stable; i.e., does not change the relative order of elements with equal keys
In-place; i.e., only requires a constant amount O(1) of additional memory space
Online; i.e., can sort a list as it receives it
What is the meaning of being O(f(x))
for some large value x, you are bounded below by c*f(n)
What is a common way to speed up exponential time algorithm 2^N for example?
Memorization, you want to save on disk previous results. It will increase space complexity but it will reduce your running time. One example is the Fibonacci series where you save the previous results on disk
Pretty good way to check if a number is a power of two or not.
def is_power2(num): ‘states if a number is a power of two’ return num != 0 and ((num & (num - 1)) == 0) https://stackoverflow.com/questions/8556206/what-does-mean-in-python
What is O() of nested loops?
O(size of the loop*size of the loop2) it is quadratic algorithm, like finding a common number in 2 arrays
What makes a pivot in quicksort a good pivot?
You want it to split the array almost in half the most balanced you can!
I.e the median of the array!
Describe selection sort
In computer science, selection sort is an in-place comparison sorting algorithm. It has an O(n2) time complexity, which makes it inefficient on large lists, and generally performs worse than the similar insertion sort. Selection sort is noted for its simplicity and has performance advantages over more complicated algorithms in certain situations, particularly where auxiliary memory is limited.
arr[] = 64 25 12 22 11
// Find the minimum element in arr[0…4]
// and place it at beginning 11 25 12 22 64
// Find the minimum element in arr[1…4]
// and place it at beginning of arr[1…4] 11 12 25 22 64
// Find the minimum element in arr[2…4]
// and place it at beginning of arr[2…4] 11 12 22 25 64 //
Find the minimum element in arr[3…4]
// and place it at beginning of arr[3…4] 11 12 22 25 64
Matrix multiplication! How fast is a naive implementation?
It is n^3 you have a n^2 number in the results and those come from a row*column multiplication so n operations!. Note that you can never do better than the input size, we have n^2 elements so if they are independent (worst case scenario) that is the best we can do
What are the 2 structures you can use to store graph? describe them
1) an adjacency matrix. With 1 or -,1 or x in i,j for simple direct or weighted graph when vertices i and j are connected. It is an O(n^2) structure which is optimal only for dense graph where you have n^2 link
2) adjacency list: there are various representations but Each list describes the set of neighbors of a vertex in the graph.
What is the minimum cut problem?
You want to compute the cut, partition graph in A, B so that we have the minimum number of crossing edges
Do you have a faster than cubic matrix multiplication algorithm?
yes, the Strassen algorithm. Remember where that comes from divding the matrix in blocks and magically using only 7 multiplication instead of 8
How many cuts (partition) does a graph of N vertices have?
2^n it is a partition into 2 so every element can either stay in A or B, so 2 possibilities than raised for the N elements. 2^n -2 (to remove the emptyy set)
What is the minimum connectivity of a vertex in a graph which minimum cut solution has k crossing edges?
K otherwise I can just cut that only vertex and I will have a partition with a smaller number of crossing edges!
What is the maximum number of minimum cuts in a graph?
(n
2)
n chose 2. This is bigger than a tree (n-1) and smaller than the total number of cuts you have which is 2^n
How would you choose the pivot in the quicksort algorithm?
You would use random algorithm!
This makes quicksort a randomized algorithm a very successful type of algorithm.
How does insertion sort work? What is time and space complexity
Swapping all the element till sorted. For all element it as to go trough the array so O(n^2) but can be doone in place so space is O(1)
Function to do insertion sort
def insertionSort(arr):
Traverse through 1 to len(arr)
for i in range(1, len(arr)):
key = arr[i]
Move elements of arr[0..i-1], that are
greater than key, to one position ahead
of their current position
j = i-1
while j >=0 and key < arr[j] :
arr[j+1] = arr[j]
j -= 1
arr[j+1] = key
Driver code to test above
arr = [12, 11, 13, 5, 6]
insertionSort(arr)
print (“Sorted array is:”)
for i in range(len(arr)):
print (“%d” %arr[i])
Time of quicksort on an already sorted array if we pick the pivot as always the first element!?
It is quadratic!! O(n^2) this is a very bad choice of pivot!
Do you get any gain in attach recursively the integer multiplication?
Only if you use the Gauss tricks otherwise if you compute all the 4 products you do not gain anything.
What is the master method or master theorem?
A quick and efficent way to get the running time in recursive algorithms. It has some assumptions: the most important is that you are breaking the size equally at every recursion
Guiding principle to analyze algorithm?
1) worst case analysis (think about the worst case given a lenght n) other options are average case and benchmark but you have to know what is the distributions of your input 2) do not care about small constants etc only O() we do this cause we care about big problems! Also they would depend a lot on the implementation!!!!
Find an unbiased estimator for the mean ?
How can you get the variance
It does not exist.
The intuition is that the median can stay fixed while we freely shift probability density around on both sides of it, so that any estimator whose average value is the median for one distribution will have a different average for the altered distribution, making it biased.
If you can sample on it you can do bootstrapping. Divinfg the dataset in batches you can get the variance as well
Is the sample of the median unbiased?
Only if the distribution is simmetric.
The sample median is an unbiased estimator of the population median when the population is normal. However, for a general population it is not true that the sample median is an unbiased estimator of the population median. The sample mean is a biased estimator of the population median when the population is not symmetric.
