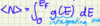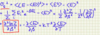Stats Flashcards
State principle of equal a priori probabilities
At equilibrium, an isolated system can be found in any of its microstates with equal probability.
What is the macrostate?
A collection of microstates with a common property; same value of that property (combinations of boxes with a common property).
Define temperature as a partial derivative
Use fundamental relation of thermodynamics (1st law with chemical potential).
What is meant by microstate?
A description of a system where all values of the dynamical variables are exactly specified
Why fluctuations in system properties are rarely observed in macroscopic systems?
- standard deviation about modal macrostate goes like 1/Sqrt(N)
- so as N-> infinity, standard dev. ->0
- hence system rarely strays from the modal macrostate
What is meant by an irreversible process?
- System and surroundings cannot be returned to original conditions when process is reversed
- due to WD against dissipative forces
- Entropy is a state function, so the system entropy change is zero, although not of the surroundings (not of the surroundings what?
Boltzmann entropy of a system
- S = klnΩ
- Ω = number of microstates of a macrostate (i.e. microstate multiplicity)
Gibbs entropy
- Pi is prob. of occupation of a macrostate
- generalisation of Boltzmann entropy
- Boltzmann only applies to isolated systems where energy is conserved
- e.g. microcanonical ensemble
- or the total sum of canonical & grand canonical ensembles i.e. the reservoir
- Gibbs -> Boltzmann
- pi = 1/Ω for all in i
- hence SB = klnΩ
- pi = 1/Ω for all in i
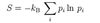
What does the Fermi-Dirac function represent?
- describes a distribution of particles over energy states in systems consisting of many identical particles
- particles obey the Pauli exclusion principle (half integer spin in thermodynamics eqm)
Conditions between system and environment that allow us to employ a microcanonical ensemble
- System is isolated with environment
- hence system cannot exchange energy or particles with its environment
- energy of system remains exactly known as time goes on
Conditions between system and environment that allow us to employ a grand canonical ensemble
- System can exchange energy particles
- hence states of system can differ in both total energy E & total number of particles N
What is a degenerate Fermi gas?
- Single particle states are occupied with probability 1 up to max. single particle energy (EF = Fermi energy)
- whilst all single particle states with E > EF are empty
- All energy levels from 0 to EF are fully occupied
- occurs at T=0 & approximately kT << EF
What happens when the temperature is much less than the Fermi temperature?
- Degenerate Fermi gas is formed when T << TF (TF = fermi temp. =EF/k)
- and also formed at absolute zero.
State the canonical partition function
- s = index for microstates of the system
- β = 1/kT
- T = temp. of reservoir
- Es = total energy of system in the corresponding microstate
What is the canonical partition function of N indistinguishable particles given single particle state Z1?
- ZN = Z1N/N!
- is the exception for identical particles
- generally the parition fn of an entire system is the product of the individual parition fns
- so if subsystems have same physical properties then
- ZN = Z1N <=> lnZN = NlnZ1
- non-interacting & distinguishable
- more generally
- Z = product of ZJ <=> lnZ = sum of ln ZJ
- for Debye model, the sum with ln ZJ is integral over frequencies
- so if subsystems have same physical properties then
What is meant by thermal equilibrium?
- 2 systems are in thermal equilibrium if they are in thermal contact
- i.e. have the same temperature.
What is the meaning of extenstivity? Which state variables in the expression for Gibbs free energy G = E + pV -TS are extensive?
- Extensive variable depend on N
- hence is proportional to the amount of the substance
- State functions are extensive
- so E, V and S are extensive
- T, p, μ are intensive
- since they stay constant with changing N
What is dG? And hence show that G = μN
- Gibbs free energy is the “free” energy available in a system to do useful work
- related to chem. pot. μ=dG/dN
- if μ is non-zero,
- particles will enter or leave system
- so G changes
- this can be shown by using 1st law at const. T and p.
What is meant by a particle bath?
- a surrounding reservoir in which the chemical potential is constant
- so there maybe exchange of particles in the system with the surroundings (reservoir)
Give an example of physical property of a degenerate fermi gas that is different from classical expectation.
.
What is the microstate multiplicity if Q indistinguishable objects are shared between N distinguishable boxes? What is the multiplicity if the boxes are indistinguishable?
- number of ways of placing Q indistinguishable items in N distinguishable boxes
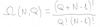
Why is it important to take into account particle indistinguishability when modelling stats therm properties of a system?
- All permutations of the particles give the same state of the system
- so leads to over-counting and degeneracy**
- for correct sum over the states, must divide by N!
- If it is a lattice => indistinguishable
- distinguishability is revelant in counting configuration
State the grand canonical partition function
- i = index of microstate
- Ni = total particle number in the ith microstate
- Ei = total enegy in the ith microstate
- μ = chemical potential of reservoir
- T = temp of reservoir
- related to Grand potential (Φ = -kTlnZG)
- whereas canonical parititon is related to F
- F = -kTlnZ
- whereas canonical parititon is related to F
What is the grand canonical partition function for fermions?
- no more than 1 fermion can occupy the same single-particle state
- N0 = 0 for E = 0
- N1 = 1 for E = ε
- so summation series ends at 1
- Z = 1 + e-(E-μ)/kT
How do you derive Maxwell equations?
- Write fundamental relations in differential form
- Rewrite as a total differential eqn
- Compare eqns
- Find the 2nd mixed derivatives (which are equivalent)
Give the equation of the heat capacity at constant volume. How do you find entropy from this?
- Cv = (dQ/dT)v = (dE/dT)v
- derived from 1st law in differential form
- dE = dQ + dW = TdS - pdV
- so at constant volume
- dE = dQ
- dQ = Cv dT
- dS = dQ/T = Cv/T dT
- Integrate dS to find S
What is meant by the thermodynamic limit? What stats property of a system exposed to heat bath is expected to vanish in this limit?
- the macroscopic limit, i.e. limit in which N –> infinity
- fluctuations in mean energy -> 0
- generally, fluctuations in system variables -> 0 in the thermodynamic limit of a particular ensemble
Thermodynamic potential and when are they used to identify an eqm state of a system?
Is this how to maximise entropy by minimising the thermodynamic potentials?
What is meant by a Bose-Einstein condensate?
- boson gas at very low temp.
- finite ratio of total number of particles occupy the single-particle ground state (hence a macroscopic number of particles in the thermodynamic limit)
- phase transition to BEC occurs at critical temp. Tc of order n2/3(ħ/mk)
- when mean interparticle distance is comparable to the thermal deBroglie wavelength
What are the different states of matter observed when particle density lies above, below or at the quantum concentration?
- above: BEC ( maybe also degenerate fermi gas)
- Quantum effects become noticeable when the particle density ≈ quantum concentration nq
- below: classical limit
What is a Boltzmann factor? Which stats ensemble employs this factor and what does the ensemble represent?
- Type of probability distribution
- employed by the canonical ensemble
- which represents a system that is able to exchange energy with its surroundings
How do you find the Fermi energy of N electrons from the density of states?
- by looking for number of electrons N, the Fermi energy EF can be extracted
How do you find the mean energy of a gas of N electrons?
- = mean energy of a Fermi gas
- also given by finding total energy (since reference energy is 0 hence total gives average) by integrating EF wrt dN from 0 to N
How does chemical potential determine how a partition might move?
- Particles move from a region of high μ to a region of low μ
- if particles move to the other side through the partition
- pressure on that side (side with more particles) now increases
- pushing the partition in the opposite direction
- hence partition should move to the side which initially had a higher μ
Deduce the Clausius-Clapeyron eqn for slope of coexistence curve on a p-T diagram.
- Given the eqn for dμ
- know that along the coexistence line, dμ1=dμ2 for the diff. phases
- at critical point Tc and pc, system equilibrates in state with min G => (dG/dN1)T,p = 0
- total number of particles, N = N1 + N2, is conserved
- therefore dN1 = -dN2
- so (dG/dN1)T,p = 0 = μ1- μ2 => μ1=μ2
- dμ1 = -s1dTc + v1dpc & dμ2 = -s2dTc + v2dpc
- s = S/N & v = V/N
- equate the differentials, and do some algebra to arrive at:
What is an appropriate dispersion relation for EM wave modes?
ω=ck
How do you calculate mean energy of radiation in frequency range ω -> ω + dω using density of EM wave modes g(ω)?
- Integrate E g(ω) dω from 0 to infinity
- E = mean energy of the QHO oscillators excluding zero point energy
- (can’t do the expectation sign here)
What is the mathematical difficulty if zero point energy was included in the calculation of total mean energy in the cavity?
- integrand for total mean energy would contain a term that is proportional to the integral of ω3 dω which goes to infinity as frequency (integral upper limit) goes to infinity
- giving infinite mean energy
What is Einstein’s Cv in limit T-> 0?
- T->0, ex -> infinity
- so ex>>1 so (ex-1)2 ≈ e2x
- so in the limit that T->0, Cv = (3Nkx2)/ex
- which is exponentially decreasing
- this does not accurately represent reality as Cv doesn’t go to zero that fast
- Debye model gives a better representation
What is Einstein’s Cv in limit T-> infinity?
- T-> infinity, x->0 so sinhx ≈ x (small angle approximation)
- then Cv = 3Nk
- agrees with classical
State Clausius and Kelvin statements of 2nd law.
- Clausius: Heat cannot spontaneously flow from cold -> hot without external work being performed on the system.
- Kelvin: No process is possible whose sole result is the absorption of heat from a reservoir and the conversion of this heat into work. (don’t get this sentence)
How does Boltzmann’s entropy account for an increase in entropy of an isolated system when a constraint is released?
- When a constraint is released, the number of system microstates now available increases
- therefore the system entropy also increases
What is the probability associated with a microstate in a microcanonical ensemble of Ω microstates?
1/Ω
because of equal a priori prob., an isolated system can be found in any of its microstates with equal probability
How do you calculate Gibbs entropy of a system described by a microcanonical ensemble?
Use Pi = 1/Ω in the Gibbs entropy formula
- because by equal a priori prob., each microstate is populated with prob. 1/Ω
State the Wiedemann - Franz law.
k = (sigma)*L*T The ratio of the thermal and electrical conductivities in metals is proportional to the temperature, through a constant L, which is independent of any microscopic or thermodynamical variable of the metal, and called the “Lorentz number”
Do we need to kno
How can photons be described as bosons?
- When you find the expression for the average occupancy of a single-particle state , you find that it is the same as that of a boson gas with chemical potential zero.
What is the Stefan-Boltzmann Law?
- gives the flux coming from a black-body at temp. T
- Flux = σT4
Describe the Einstein model and how to arrive at the heat capacity Cv.
What are phonons?
- Lattice vibrations which are excited modes of acoustic standing waves in solids
What are the factors included to account for degeneracy in the density of states?
- Multiply by spin multiplicity (2S +1) for any quantum gas
- For photons, multiple by 2 to account for the 2 polarisations ( 1 trans. + 1 long.) with the same wave-vector
- For phonons, times by 3. There are 3 polarisations (2 trans. + 1 long.)
What are the 2 assumptions the Einstein model is based on?
- Each atom in a lattice is an independent 3D QHO
- All atoms oscillate with the same frequency
How does the Debye model improve on the Einstein model?
- heat capacity found using the Einstein model (using canonical ensemble) fails at low temp. T -> 0
- Debye assumed lattice vibrations can be modelled as phonons and derives their density of states
Describe how the ultraviolet catastrophe arises in photon gases? How is it remedied?
- energy of the QHO’s contains the zero-point energy which is also included in the canonical partition function
- when finding the mean energy, infinites arise from the zero - point energy
- since integral is over frequencies which tend to infinity
- remedied by assuming the zero-point energy is of no thermodynamic interest and neglecting it
- alternatively, a cut-off frequency can be introduced
What is necessity of the Debye frequency?
- (Similar to the ultraviolet catastrophe)
- number of phonon modes depends on frequency, which goes to infinity with frequency
- since there are 3N QHOs (clearly finite) this cannot happen
- Debye introduces cut-off frequency to keep the number of modes finite
When does the grand canonical ensemble become equivalent to the canonical case?
- chemical potential of the particle bath = zero i.e. μ=0
- there is no longer particle exchange
- only energy exchange = canonical ensemble
Explain why the canonical partition function of a system depends on whether the particles are fermions or bosons?
Describe how the entropy decreases as the temperature is reduced at constant volume.
Describe how the occupation of the lowest energy single particle state of the system evolves as the temp. is reduced from Tc to zero.
Deriving the density of states for
- fermions
- relativisitc regime
- photons
- k = nπ/L
- each spatial direction has wavefn quantised as k
- so number dN of single particle states in a wavevector interval k -> k + dk is:
- dN = (L/2π)d
- d = no. of dimension
- 2 because only +ve
- each length contributes 1/π
- dN = (L/2π)d
- for d = 3
- dN = (V/8π3) dkxdkydkz
- switch to polar coordinates then dkxdkydkz = |k|2dk sinθdθ dφ
- integrated over domain [0,π/2] which spans the octant of +ve kx, ky, kz
- so dN = (V/2π2) |k|2dk (why 4π? - elemental volume)
- then dN = g(k) dk
- sub E = ħ2k2/2m and multiply by spin multiplicity (2S+1)
- sub E = khc
- sub ω = kc and multiply by 2 for polarisation vectors (trans & long)
- Calculate the number of single-particle states between k -> k + dk : Elemental volume 4Pi*k^2 *dK, divided by volume of each lattice point, (delk)^3 = (Pi/L)^3
- Divide elemental volume by 8 since considering positive quadrant
- Equate g(k)dk=g(E)dE –> g(E) = g(k)dk/dE
- Sub. in expression for E and calc. dk/dE
- Multiply by the degeneracy factor - in this case, spin multiplicity.
What is meant by thermal equilibrium?
System and surroundings, perhaps another system, are at the same temperature, where temeperature is the defining feature of thermal equilibrium. This is precisely examined in the zeroth law.
Aside from changing its temperature, how might a degenerate fermi gas be made to behave classically?
- EF grows with particle density, n
- so a degenerate fermi gas may arise at any temperature provided that n is high enough
- In this case, lowering n lowers TF (so it should be provided that n is low enough?)
- so it can be forced to become classical
What are the minimum and maximum values for average N in a single-particle state?
- min = 0
- max = N (isn’t it 1?)
What is the mean energy in the ensembles and how do you derive it?
- (1/Z) Σe-βEi = 1 because of the way the partition function is defined in terms of probabilities
- Pi = (1/Z) Σe-βEi
- probability of specified microstates = sum of microstates/parition fn (which represents all microstates)
- parition fn Z plays the role of a normalising constant to ensure probabilties sum up to 1
- Pi = (1/Z) Σe-βEi
- and sum of all probabilities = 1
What is the variance in energy?
What are the 4 laws of thermodynamics?
- Zeroth: if 2 systems are in thermal eqm with a 3rd then they are all in thermal eqm with each other
- state fn T may be defined
- First: There exists a state fn E that is conserved in isolated systems
- Second: State fn S that either grows or stays constant in isolated systems
- Third: S is 0 at absolute zero of T
What is the mean number of particles/oscillators in system over grand canonical ensemble?
- (1/kT)T partial derivative means kT is constant so comes out of differentiation
- derivative of lnZ wrt x always give (1/Z)(dZ/dx)
How to switch variables (ones that differentials depend on) from the fundamental relation of thermodynamics (S,V,N)?
- Write other thermodynamics potentials in differential form
- dF = -SdT-pdV+μdN
- dH = TdS+Vdp+μdN
- dG = -SdT+Vdp+μdN
- dφ = -SdT-pdV-Ndμ
How to maximise S if the constraints on the system are
- T & V
- S & p
- T & p?
- a thermodynamic process starts with a system under certain constraints
- system evolves to new eqm state that maximises total entropy change when constraints are changed
- different thermodynamic potentials allow different expressions of maximising entropy depending on the contraints
By minimising
- F (T,V,N)
- H (S,p,N)
- G (T,p,N)
What are the characteristics of Debye solids?
- Heat capacities
- = 3Nk (high T regime)
- proportional to T3 (low T regime)
- similarities with photon gas in expressions for E & S in terms of T
How can you tell from the mean number of particles integral involving density of states whether it is a boson or fermion?
- g(E) gives density of 1-particle states in E->E+dE
- N<span>E</span> gives average number of particles in this interval
- N is the average of these averages
- for bosons, due to -1 in denominator, it is required that μ<e>E > 0</e> i.e. physical
- otherwise NE < 0 is unphysical
- (Ns should have expectation brackets around them)
What does mechanical equilibrium imply? If gases are also in thermal equilibrium, what does this imply?
- their pressures are the same
- so p can be treated as a constant
- their temperatures are the same
- so T can be treated as a constant
What is internal entropy generation?
- In non-quasistatic adiabatic processes
- ΔSres = 0 but ΔStotal > 0
- means that ΔSsys > 0
- this is due to internal entropy generation
What does a reduction in entropy imply?
- less uncertainty in the position microstate for gases
- better idea of where to look for them & more likely to
- decrease uncertainty => entropy decreases
What is the entropy change for quasistatic processes (system in thermal contact with reservoir)? And work done? What is the entropy and WD if the process was non-quasistatic?
- ΔStot = 0 = ΔSres + ΔSsys => ΔSres = -ΔSsys
- ΔE = 0 (thermal contact) => ΔW = -ΔQ
- ΔSres = -ΔQ/Tres
- hence ΔW = TresΔSres
- For non-quasistatic, total entropy change must be > 0
- & ΔSsys will not change because ΔSsys is a state fn
- so ΔSres has to increase
- => ΔW has to increase
Define the microcanonical ensemble (describes isolated system)
- all microstates with a certain given energy taken with same probability
- if E is not specified
- take a “microcanonical average” whih means taking all possible microstates with same probability
What is the Gibbs entropy of a canonical ensemble?
State the 1st and 2nd law in differential forms
- dE = dQ + dW
- ΔStot = ΔS + ΔSres
What is an adiabatic process?
- one where no heat is transferred
- ΔQ = 0
What is a quasistatic transformation?
- one where system & reservoir are always infinitely close to eqm
- so all state fns may be defined along transfomration
- or where ΔStot = 0
- N.B. It is always true that ΔSr = -ΔQ/Tr
- even if it is not quasistatic
What are the 4 laws of thermodynamics?
- Zeroth: 2 systems thermal contact with 3rd all in thermal eqm
- define state fn T
- First: state fn E conserved in isolated systems
- Second: state fn S either grows or stays constant in isolated systems
- Third: S (T=0) = 0
Why 1/N!?
- particle indistinguishability
- so all permutations of these particles give same state
- = overcounting
