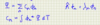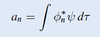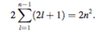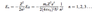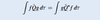Quantum Flashcards
State TDSE.
- μ = reduced mass
- usually just mass of the particle
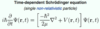
State TISE.
- μ = reduced mass
- usually just mass of the particle
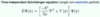
How do you obtain TISE from TDSE? What is the physical interpretation of constant E?
- Ψ(x,t) = T(t)ψ(x)
- separation of variables
- each indt term equals E
- both constants have to be equal
- E = total energy = sum of KE + PE
What is the time soln to TDSE?
T = e-iEnt/ћ
What is the significance of |Ψ(x,t)|2?
- probability of finding the particle at posn x
- stationary states => |Ψ(x,t)|2 associated with the wavefn of the state is indt of time
When is |Ψ(x,t)|2 expected to be indt of time (i.e. a stationary state)?
- When the potential is indt of time
- only then can the wavefn be split into time and space parts
Define the commutator between 2 operators A and B.
[A, B] = AB - BA
What are the implications of 2 operators if they commute?
- compatible operators
- so can be simultaneously measured
What is the angular momentum operator? Show commutation relation between operators for posn and momentum for particle moving along x is iħ
- x =x & Px = iħ∂/∂x
- [x, Px] = xPx - Pxx = iħ∂x/∂x = iħ
- L is important for 3D problems involving central potentials (potentials that depend only on radial coordinate r)
What is the definition of a Hermitian operator? Give examples of Hermitian operators.
- H = T + V
- T = p2/2m = KE operator
- V = V(x) = PE operator
- What other examples are there?
Prove eigenvalues of Hermitian operator are real.
- write eigenfn equations for the operator
- also write the complex conjugate eigenfn equation for the complex conjugate operator
- equate fns in definition with eigenfns from the equations above
- evaluate LHS and RHS separately
- show that qm = qm*
Explain the physical significance of n, l, m and give their possible values.
- n = principal quantum number
- energy => energy observable H
- n = 1, 2, 3 …
- l = angular momentum quantum number
- magnitude of angular momentum
- l = 0, 1, 2, …, n-1
- corresponds to operator L2
- m = magnetic quantum number
- component of angular momentum along chosen axis
- |m| less than or equal to l
- -l , .., 0, …, l
- corresponds to operator Lz
What is the notation 5f, and how many states correspond to these?
- nl notation
- n = 5
- p => l = 3
- so m = -3, -2, -1, 0, 1, 2, 3
- giving 7 states
- so m = -3, -2, -1, 0, 1, 2, 3
How to deduce L2 measured would be equal to an eigenvalue given the normalised angular wavefn?
- L2 eigenfn equation:
- L2 Y = l(l+1)ħ2 Y
- find l by solving quadratic eqn
- normalisation factor = an
- probability given by |an|2
=> probability of getting eigenvalue l(l+1)ħ2 is |an|2 of Ylm corresponding to that eigenvalue
Work out expectation value of Lz given a normalised angular wavefun.
- eigenvalues of Lz = mħ
- expectation value of Lz = Σ |an|2mnħ
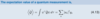
General form of solns to TISE for E > V0 in finite square well
- same as that of a free particle
- different wavenumber
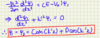
General form of solns to TISE for a free particle.
What must the form of the equation be inside a potential barrier?
Exponential decay for the values of x
When is it more appropriate to use sin and cos instead of exponentials?
- inside finite square well
- inside infinite square well
Reflection probability
- reflection coefficient = sqrt(R)
- reflection probability = R
- = |reflected flux/incident flux|
Transmission probability
- transmission coefficient = sqrt(T)
- transmission probability = T
- = |transmitted flux/incident flux|
What is the general form of the wavefn in a periodic array of delta fn potentials?
What is the periodic boundary condition?
How can you deduce that a wavefn is an eigenfn of an operator?
If the wavefn is proportional to the operated wavefn
What are compatible operators?
- if the operators commute
Quantum theory of measurement
- λn = results obtained by measuring a physical quantity that corresponds to operator A
- immediately after measurement, the system is in eigenstate (eigenfn) φn associated with eigenvalue λn returned from measurement
- probability of measuring λn = |Cn|2
- averages obtained after many measurements on identical particles = expectation value
- expectation value of a quantum measurement is:
- = integral of ψ*Aψ dT = Σn |Cn|2 λn
- if the solns to TDSE are stationary
- eigenfns are orthonormal if
- integral of φn*φm dT = δm,n
What is meant by tunnelling in QM? Also why does it play an important role in nuclear fusion and alpha decay?
What is meant by an orthonormal set of eigenfns?
- eigenfns are orthogonal to each other
- eigenfns are normalised
State 3 conditions solns to the Schrodinger equation (SE), wavefns, must satisfy to be physically acceptable
- ψ & ψ’ must be continuous at boundaries
- normalisable (finite normalisation integral)
- single-valued
Give an eigenvalue eqn other than SE.
- L2Y = l(l+1)ħ Y
- gives magnitude of angular momentum
- LzY = mħ Y
- gives component of angular momentum along a given axis
What is the TISE for QHOs?
- particle on a spring
- => Hooke’s law with restoring force F=-kx
Sketch ground state wavefn of QHO and give 2 ways in which the QHO differs from classical equivalent.
- energy spectrum is quantised
- minimum energy is not zero => zero point energy = E=(1/2)ħω
Exponential decay beyond classical limit
Give the 3 approximations made when solving SE for periodic potentials?
- Born-Oppenheimer approx: Electron motion w.r.t fixed nuclei
- One electron approx: Each electron moves in a periodic potential due to fixed positive ions.
- 1D: Consider only one dimension, rather than 3.
State Bloch’s theorem.
The eigenfunctions of the SE for electrons moving in periodic potentials is the product of the free particle plane wave and a function u(x) with the periodicity of the lattice. Wave functions of this form are called “Bloch wave functions”.
What is the interpretation if the TDSE solution in terms of travelling waves?
Which terms are neglected in the radial SE for r-> infinity and r-> 0?
- In the limit far from the nucleus, the effective potential term goes to zero and we have a free particle.
- Close to the nucleus, the angular momentum term l(l+1)/r^2 dominates in the potential.
- 1/r term is the coulomb potential term and 1/r^2 is the centrifugal term.
What is flux?
- mean number of particles passing a point per unit time
When the width of the square well is changed, how do we find the probability of occupying a given eigenstate?
- Original wavefn not defined for new width, only for old width, e.g if changed from ±a, to ±3a, take coefficient integral from ±a, since fn defined for this range.
- expansion postulate - find coefficient of eigenstate
- Take square mod of coefficient.
Explain why eigenfns of one operator might be eigenfns of another operator
- if the operators commute
- i.e. they are compatible
- i.e. their commutator = 0
- which means they can be measured simultaneously with certainty
- and they share common eigenfns
How do you obtain coefficients for above step potentials i.e. E>V0?
- region before potential barrier
- plane wave incident has amplitude 1
- since assume a particle per unit length
- travels to right so +ve x in exp
- reflected at barrier is possible
- reflected wave at barrier with reflection coefficient
- travels to left so -ve x in exp
- plane wave incident has amplitude 1
- after potential barrier
- transmission to another region
- k changes to k’
- no incident wave travels to the left
- if d2ψ/dx2= 0
- dψ/dx = C (const.)
- ψ = Cx + D(another const.)
- if d2ψ/dx2= 0
- so coefficient with -ve x in exp = 0
- transmission to another region
Obtaining K=ktan(ka)
- match boundary conditions
- find 2Acos(ka)
- find 2kAsin(ka)
What is an eigenfunction? What is an eigenvalue?
- A function that when operated on returns itself & a multiplicative factor
- The multiplicative factor is the eigenvalue
What was deBroglie’s relationship between momentum and wavelength?
p=h/λ=ħk
State the heisenberg uncertainty relation for position and momentum.
Explain briefly why measuring an electrons position through compton scattering with high energy photon leads to uncertainty in the knowledge of the electrons momentum.
- In scattering a photon of the electron, the uncertainty in the electrons position depends on the wavelength of the photon.
- The smaller it is, the more accurately the position is known.
- High energy photons have a higher momentum, and cause a larger change in momentum of the electron.
- Therfore, the more accurately the position is known, the less accurately the momentum is known.
Why can a wavefn be expressed as a Σnanφn?
- eigenfns form a complete set meaning any fn satisfying same boundary conditions are linear combinations of total wavefn
What are the possible values of spin quantum numbers s and ms for e-?
- s = 1/2
- ms = -1/2, +1/2
What are the possible values of total angular momentum quantum number j that can be produced by combining l and s? What is the range of total magnetic quantum numbers mj?
- |l-s| < j < |l+s|
- in steps of one
- those should be .. than or equal to
- |mj| < j
- in steps of one
On which quantum number does energy depend and what is the functional form of this dependence?
- Energy depends on n.
What main compton scattering features contradict classical physics?
- Upon scattering of particle, photon energy is reduced => wavelength increases.
- Wavelength shift detected
- photon momentum change
- photon behaves as a particle
Explain compton scattering.
- beam of photons have associated momentum - hbar*k
- electron momentum - mv
- photon scatters from electron
- total momentum and energy conserved Pfin=Pini
- photon exchanges momentum with electron
- electron recoils
- photon momentum reduced
- since photon speed invariant, wavelength must change
*
Physical interpretation of E_n.
- En are the energies of the eigenstates.
- Energy eigenvalue corresponding to nth eigenfunction.
Define expectation value.
- The average value of a set of repeated measurements on identical systems
Expression for expectation of an operator in terms of of Cn and its eigenvalues.
Describe the Stern-Gerlach experiment.
- Produce beam of s-state atoms
- l=0, so no orbital ang. mom. interaction with field
- Apply inhomogenous mag. field
- Force on particles is:
- 2 groups of atoms deflected in opposite direction => experience different forces
- Force must be due to some ang. mom. whose direction has 2 states => spin
What feature of compton scattering disagrees with classical?
- Wavelength shift.
For non-compatible operators P and Q, if P is first measured giving its eigenvalue p, then Q is measured giving q, if P is measured again, what are the results of measurement?
You may yield p again, but this is not certain as P maybe in any of its eigenstates, with some associated probability.
What is meant by tunneling?
- In classical physics, a particle with energy less than the barrier potential cannot cross the barrier.
- In QM, there is a finite probability that the particle may cross this barrier, “tunnel”.
- Arises from continuity of wavefunction at the boundary.
Why does harmonic potentials energy eigenvalues have x dependence?
Since potential increases with x
What are the origins of n,l and m?
- n - quantisation of energy
- m - φ returning to its original value after 2π
- l - need for legendre polynomial to converge
Show that the components of angular momentum do not commute.
Postulate 1
- Exists wavefn which is continuous, single valued, square-integrable, normalisable.
- Depends on all system param.
- Gives all possible predictions of system properties
*
Postulate 2
- Each observable has an associated linear hermitian operator
- Operators are related by classical eqns.
- operator has real eigenvalues and orthogonal eigenfunctions
- immediately fater measurement, wavefn collapses to eigenstate corresponding to eigenvalue.
Postulate 3
- Operators are related to each other in the same way as in classical mechanics.
- Staring point are R and P operators.
Postulate 4
- Wavefn can be expanded as a linear combination of its eigenfunctions.
- This is because they are orthonormal and form a complete basis
- The mod. square of the coefficients of the eignefunctions give the probability with which each eigenstate is occupied.
Postulate 5
- Between measurements of the system, the time-evolution of the wavefn is governed by TDSE.
