EM Flashcards
State Gauss’s Law in integral form (for free charges)
- E = electric field vector
- dS = elemental surface vector
- qenc = total charge contained within closed surface S
- ε0 = permittivity of vacuum
- net flux through any closed surface is proportional to charge enclosed
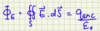
Define potential and give the eqn in integral form
- WD per unit +q from infinity to posn vector against E field
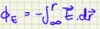
State Biot-Savart Law and define parameters
- ds = elemental length of conductor carrying electric current I
- r hat = unit displacement from current element to field point
- I = steady current flow in current element
- r = distance from current element to field point
- B(r) = resultant magnetic field B at posn r generated by steady current I
- dB = elemental resultant magnetic field

Problem solving strategy steps for Biot-Savart Law
- Posn vector of current source point which is = r’
- Expression for elemental length vector ds (depending on coordinate system); ds = (dr’/dx’) dx’
- Posn vector of field point P which = rp
- Find r hat by finding the relative position vector: r = rp - r’
- Cross product of ds & r hat
- Simplify dB by rewriting dependent variables in terms of each other and integrate dB with correct limits
Problem solving strategy steps for Gauss’s Law
- Identify symmetry; cylindrical? planar? spherical?
- Direction of E
- Draw an appropriate Gaussian surface on which magnitude of E is constant over surface
- Calculate qenc, charge enclosed by Gaussian surface
- remember to change volume for charge from charge density distribution
- Calculate electric flux using surface integral of E.dS over Gaussian surface
- Apply Gauss’s law to find E
Problem solving strategy for Faraday’s law
- Identify symmetry; define area vector A & let it point in direction of thumb (right hand rule)
- Calculate magnetic flux through loop using
- B.A for uniform B
- surface integral of B.dA for non-uniform B
- Differentiate the mag. flux w.r.t time; which can be caused by
- dB/dt
- dA/dt
- dθ/dt
- Multiply by -1 to get induced emf
Divergence theorem
.

Magnetic moment of a loop and give direction of the vectors
- vector quantity with direction perp. to current loop in right hand rule direction and parallel to area vector A
- determines torque it will experience in an external B field

State Kirchoff’s second law and what it means physically
-
sum of the potential differences around a closed loop is zero
- n = total number of voltages measured
- consequence of principle of energy E = ½QV
- potential is defined as the potential energy per unit charge, the increase in potential energy for a single charge, but must be equal to the decrease in energy, which is not possible –> conservation of energy
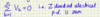
Electric field equation for known potential function VE

What is meant by Principle of Superposition?
- Force experienced by one charge due to another is unaffected by the presence of other charges
- therefore the total force on a single charge due to a configuration of charges = sum of the individual forces

State Faraday’s law of induction and its equation
- induced EMF in any closed circuit = -ve rate of change of magnetic flux enclosed by the circuit
- a time-varying B field is always accompanied by a spatially-varying, non-conservative E field & vice versa
- for N loops, total induced emf is N times as large

Derivation of Gauss’s law
Total outward flux over a closed surface in a vacuum
- Find E.dS
- Notice that one part gives dΩ (solid angle)
- Integrate over solid angle to give 4π

Describe the E field and charge distribution within a cyclindrical capacitor
- inner cylinder has +ve charge density +λ
- since E field in a conductor = 0, the inner surface of the outer cylinder has -ve charge density -λ
- unless there is charge inside the inner cylinder, the E field inside it is zero? (field existed inside a conductor; pd caused by that field would cause mobile charges to flow as current & build up to cancel external field within conductor)
- outside of capacitor, the E field is also zero
- if there is free space (where charges cannot flow) between inner and outer cylinder then Einner cylinder extend across gap to inner surface of cylinder
- this E field causes charges to rearrange themselves in the cylinder
What is the surface charge density on the inner surface +λ of the conducting cylinder of the cyclindrical capacitor?
- E = σ/ε0
- σ = λ/2πε0

What is the potential difference of the cylindrical capacitor?
.

How is power stored or released during a full cycle in an inductor?
- switch opened; current through the inductor = 0
- switch closed; current in the circuit increases with time to its max. value in circuit
- plateaus at the max. value
- max. energy has been stored in the capacitor where it plateaus
- i.e. E is stored in B field as current builds
- due to WD against inductance in the charging process?
- switch reopened; E stored in B field is released
- i.e. E later released to circuit as current falls
- current decays to zero
How do you find the current in a purely inductive circuit?
- Kirchoff’s rule gives eqn for voltage drop across inductor
- rearrange & integrate to find current
- C = infinity & R = 0
- IL0 = VL0/XL (reactance defined by integrating: X<span>L </span>=<span> </span>ωL)
- increases with frequency
- higher frequencies current changes more rapidly
- hence more opposition to current change
- increases with frequency

Difference between polar and non-polar molecules
- Polar has permanent dipole in absence of external E field
- Non-polar do not have permanent dipole (centre of gravity of nucleus & e- cloud are in same place)
What is meant by electrical conductivity? How it relates current density and electric field in a conductor?
- measure of a material’s ability to allow the flow of electrical current
- high J & low E => high conductivity
- resistivity = reciprocal of conductivity
- ρ = RA/L

Why is the rate of the change of total energy for a LC circuit zero?
- switch closed; capacitor discharges & electrical energy is decreased
- but this causes a flow of current through the inductor
- hence magnetic energy generated and stored in the inductor
- => total energy in an LC circuit is constant
- charges flow back & forth between plates of capacitor & through inductor hence E oscillates back & forth between capacitor & inductor
- also assumes no resistance => no dissipation of energy
Equation for capacitors in series and in parallel
- series; V different for each capacitor & current same
- parallel; V same & current different for each capacitor

What is meant by induced dipole?
- External E field causes a displacement of charges in non-polar molecules
- hence electric dipole moments induced in molecules
Potential difference between parallel plate capacitors
- V = E d
What is the effect of a dielectric on E field? Why?
- Reduces E field by factor εr (dielectric constant)
- E field induces dipoles in dielectrics which have their own associated E field
- and dipoles are aligned with Eext (so polarisation P is parallel to Eext)
- and direction of dipoles point from -ve to +ve
- hence average E field due to these dipoles Ep is antiparallel to Eext
- => reduces total field strength
How applying electric field and magnetic field together can be used to select particles with a particular velocity and particular charge?
- e-s pass region where there exists a downward uniform E field (+ve to -ve) hence will be deflected upward
- experiences an upward electric force of magnitude ev
- apply B field directly into page
- e-s experience an additional downward magnetic force of magnitude evB
- 2 forces are in balance i.e. ev = evB
- e-s will move in a straight line
- hence only particles with speed v = E/B will be able to move in a straight line and are selected
Name 3 classes of magnetic materials and explain briefly what determines their response when brought near a bar magnet.
- Diamagnetic materials (repelled)
- Paramagnetic materials (weakly attracted)
- Ferromagnetic materials (strongly attracted)
Response dictated by χm (magnetic susceptibility)
- +ve χm = material is attracted to the external field
- -ve χm = repelled

State Gauss’ Law in differential form
- derived by applying divergence theorem to integral for electric flux in Gauss’s law
- and knowing that volume integral of volume charge density gives total charge
- equate expressions inside integrals

Force on a current carrying wire in a magnetic field
- direction of l = direction of conventional current flow I
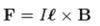
For each component in LCR circuit give phase relationship of V with I.
- IL lags V by π/2
- Ic leads V by π/2
- IR is in phase with V
Determine resistances in series using Kirchoff’s Laws
.
Determine resistances in parallel using Kirchoff’s Laws
.
Define inductance (hence self-inductance and mutual inductance) and give equation involving emf
- when a change in current flowing through a conductor creates a voltage (EMF)
- in the conductor itself (self-inductance)
- in any nearby conductors (mutual inductance)
- EMF generated to oppose a given change in current
- units: H

How do you find the current in a purely capacitative circuit?
- Kirchoff’s loop rule
- I = dQ/dt
- R = 0 & L = 0
- IC0 = VC0/XC (reactance defined by differentiaing: XC = 1/ωC)
- reactance diverges as frequency goes to 0

State the four rules of electric field lines drawing
- Field lines go from +Q to -Q
- No. of field lines is proportional to the magnitude of charges
- Field lines never cross (otherwise field would point in 2 directions at the same point)
- If total charge non-zero, lines begin or end at infinity
- Field lines drawn parallel (tangential) to E field vector
What is electric flux?
Number of E field lines per unit area through a surface; proportional to magnitude of E
What is meant by a capactior? State the equation for capacitance
- A capacitor is a device that stores electric charge
- C = Q/V
- Q = magnitude of charge stored on each plate
- V = magnitude of voltage between plates
What is meant by the “Method of Images”?
- An application of Uniqueness Theorem
- complicated configuration of charges can be replaced by a simpler configuration as long as they are identical in the region of interest
- configurations cannot be treated the same outside this region
What is meant by “drift velocity” for a current in relation to velocities of individual charges?
- average speed vd at which the charge carriers move in a conductor; average of velocities of the individual charges
- flow velocity that an electron attains due to an E field
- Iavg = dQ/dt = nqAdx/(dx/vd) [distance = speed × time]
- => Iavg = nqAvd
- so J = Iavg/A = nqvd
- n = charge-carrier density & q = charge on charge-carrier
What is the expression for current density J? How is current I determined from current density?
- electric current per unit area of cross section
- J = I/A = q ne vd = σ E
- ne electron density
- vd drift velocity
- σ conductivity

Why is the charge on the capacitor plates larger with dielectrics in between the plates for a fixed voltage? What is the new charge on the plates?
- dielectric decreases E field between plates by εr (dielectric constant)
- C is inversely proportional to E, it increases
- hence Q increases for a fixed V since C is proportional to Q
- C0 = ε0A/d
- => Cr = εrC0
- Therefore Q = CrV
What is meant by electrostatic potential energy? Describe how the equation is derived.
- consider 2 charges q1 and q2
- if potential due to q1 at point P (where q<span>2 </span>is) is V1 = q1/4πε0r12
- then WD W2 in bringing q2 from infinity to P is W2=q2V1 (because no WD in setting up q1 so W1=0)
- W2 = q1q2/4πε0r12 which equals the PE of the system
- if both charges have the same sign then +ve WD to overcome electrostatic repulsion
- otherwise -ve WD due to attractive force between charges
-
add 3rd charge q3 then W3 = q3(V1+V2) = U12 + U13 + U23
- => total PE is simply sum of contribution from distinct pairs
- then generalise for a system of N charges

Why is electricity transported via high voltage transmission and alternating current?
.
State Poisson’s equation.
- E = electric field
- V = electric potential
- ε0 = permittivity of vacuum
- ρ = charge density

What is meant by Uniqueness Theorem for electrostatics?
- For Poisson’s eqn, there is one soln that satisfies a large class of boundary conditions (one soln to Poisson that satifies boundary conditions => Uniqueness theorem)
- in electrostatics, if an E field satisfying boundary is found then the E field is complete i.e. one such soln found = complete field
State equations for equivalent resistances of capacitor and inductor.
- XL = ωL
- B field resists change of current
- XC = 1/ωC
- E field resists change of voltage
- ideal inductors and capacitors have 0 resistance
What is meant by a phasor diagram? How is it used to determine magnitude and phase of total voltage drop across 3 components in series?
- A phasor is a rotating vector
- Length of phasor = magnitude (amplitude)
- Vertical projection (sinωt) = value of alternating quantity at time t
- Sum of the phasors across all 3 components
- Remember that current phasor I0:
- leads VC0 by π/2
- lags VL0 by π/2
- therefore VC0 is in antiphase with VL0
- total voltage amplitude from working out the magnitude of the vector V0 (Pythagoras)
-
phase of total voltage drop from using trig
- hence tan(φ) = VR0/(VL0 - VC0)
- 3 voltage phasors rotate counterclockwise with time but relative positions fixed
How do you determine C given current, resistance voltage, inductance voltage?
From the magnitude of total voltage drop across all 3 components
State equation for equivalent resistance of LCR circuit.
- Effective resistance is impedance
- Re(Z) = R (resistance)
- Im(Z) = X (reactance)

Draw a graph of how I and V vary with time given initial conditions and phase difference between I and V of the LCR circuit.
.
How do you calculate natural frequency of LCR circuit given inductance?
- Resonance occurs when impedance is at min i.e. when XL = XC
- equating the 2 gives ω0 = 1/sqrt(LC)
- Z=R at resonance
- so amplitude of current is I0 = V0/R
- so φ = 0
Sketch and explain charge distribution (using Gauss’s Law and a Gaussian surface), E field, electric potential in, on and around a +ve conducting sphere.
.
Show E is a conservative field. What is meant by a conservative field?
.
How to determine radius of motion given KE, q and B?
.
What is meant by “free space”?
- space devoid of matter
- no charges
- no currents
- no polarisation charges
- no magnetisation
- where EM radiation travels at c
- Maxwell’s eqns changes
What is the physical interpretation of Maxwell’s equation for showing how E fields can propagate in space?
.
How does Maxwell equation give the speed of light?
State Ampere’s Law in integral form.
- for any closed loop path
- product of sum of length elements of B field in direction of length element is proportional to electric current enclosed in loop

Problem solving strategy for Ampere’s Law
- Identify symmetry; circular? rectangular?
- Determine direction of B field; clockwise? anticlockwise?
- Draw Amperian loop along each part which B field is constant or 0
-
Calculate current through Amperian loop by calculating it
- as a fraction of total current
- or using current density J then multiply by the area enclosed
- Calculate line integral of closed loop of B.ds
- Solve for B
Determine B field between 2 parallel wires carrying current in same direction at a point that is 1/3 from one wire.
.
What is an inductor?
An inductor is a circuit device that stores energy in a magnetic field. See Faraday’s law card for further information.
Describe mutual inductance.
- If 2 coils are placed next to each other, and the current flowing through one changes in time
- changing magnetic field produced by this coil causes a time-varying flux to pass through the 2nd coil => induces an emf
- rate of change of flux through 2nd coil is proportional to rate of change of current in 1st coil
- proportionality constant = mutual inductance
What is self-inductance?
When there is a changing current in a coil, its own changing mag. field induces an emf inside the coil to oppose the change in flux. (The emf is proportional to the rate of change of current in the coil - proportionality constant is L)
Self - inductance maths
Use faraday’s law for the emf. Since the emf is proportional to the rate of change of current, equate these two. L is the proportionality constant and has the form:
Energy stored in an inductor
- As the inductor serves to oppose any change in current, to establish current in the inductor, work is done
- this is stored as energy in magnetic field
State Kirchoff’s first law and what is the physical interpretation of it?
- at any node (junction):
- n = total no. of branches with currents flowing towards or away from node
- consequence of conservation of electric charge
- current flow is just the rate of change of charge
- if this law were not true
- charge would accumulate at the junction and current would not flow steadily

Properties of a Diamagnetic material
- no permanent dipole moment
- external B field induces a field inside a magnetic material Bm
- in diamagnetic, this field opposes external B
- hence reduces total B => suspectibility is -ve
- repelled by external magnet
Properties of a Paramagnetic material
- permanent dipole but randomly oriented hence weak interaction
- external B field aligns moments but alignment easily affected by thermal motion
- increase T -> reduced induced field in material
- weakly attracted when near bar magnets
Properties of a Paramagnetic material
0
Properties of a Ferromagnetic material
- Permanent mag dipole moment, already aligned – permanent magnet
- Alignment extends over small regions called domains
- these are randomly oriented
- If external field strong, domains become parallel to field
- if weak, mag moments align with field
- At high temps, loses permanent mag. and becomes a paramagnet.
Laplace’s equation
.
Ways to use Poisson’s eqn
.
What is meant by electrostatic eqm?
- No net flow of electric charge or electric current
- E field inside a conductor at electrostatic eqm = 0
- If E internal was not 0 then free charges inside conductor would move hence contradicts electrostatic eqm
What is electric charge density? How would you find the charges from the dimensional charge densities?
- electric charge per n dimensional volume of space
- Q = integral of dq

What is the electric field between 2 parallel plates?
- It’s also E = V/d

Define potential difference
- WD per unit charge +q against the E field to move charge between 2 points
- V = work done/charge
What is the Lorentz force law?
- measured E field depend on reference frame
- in rest frame of charge; E = F/q
- hence E is defined as electric force per unit charge
- charge moving relative to source will experience part of the force as magnetic force

What is Ampere-Maxwell’s law in differential form?

What is Ampere’s law for steady currents in integral form?
- line integral of magnetic field around a closed path is proportional to total current (free + bound) Ienc passing through surace S enclosed by C
- J = total current density
- => Ienc = surface integral of J.dS

What is Faraday’s law of induction in integral form?
- E = electric field
- B = magnetic field
- ds = elemental vector of closed contour C
- dA = elemental surface vector

What is the energy density of an E field of continuous charge distribution?
- energy per unit volume

What are the properties of a conductor?
- E field inside a conductor = 0
- any net charge must reside on surface of isolated conductor (because of Gauss’s law since E inside = 0)
- surface of a conductor = equipotential surface
- tangential (parallel to surface) component of E field on surface = 0
- just outside conductor, E field is perp. to surface & has magnitude = σ/ε0
What is a steady current?
- Continual flow of charges which is constant in time
- charge neither accumulates nor depletes at any point
What is complex impedence?
- Z = R + iX
- tanΦ = X/R
- phase difference between voltage & current
- |Z| = sqrt(R2 + Z2)
- impedence
- tanΦ = X/R
Problem solving strategy to calculating electric potential and hence electric field
- dV = dq/4πε0r
- dq =
- λdl
- σdA
- ρdV
- specify an appropriate coordinate system
- express r & differential element (dl, dA or dV) in terms of coordinates
- Rewrite dV & integrate with new limits of integration variable
- E field can be calculated using E = -grad(V)
Problem solving strategy for calculating capacitance
- Identify direction of E field using symmetry
- E field everywhere using Gauss’ Law
- ΔV = Vb - Va = -ve integral of E.dr from a to b
- Calculate C using C = Q/|ΔV|
What is the PE associated with magnetic moment? What is the effect of the torque on a magnetic moment?

How to sketch B field lines?
- N->S
- Tangent to field lines = local direction of B
- density of lines = |B|
- Lines CANNOT cross
- Lines are CONTINUOUS
How to modify Gauss’s law with dielectrics?
- electric flux = total charge, which is = conduction charges + polarisation charges
- polarisation charges = -ve surface integral of P.dS
- P = polarisation vector = dp/dV
- = electric dipole moment per unit volume
- also P = ε0χeE
- Rearrange so surface integral equals only conduction charges
- thus electric displacement field D is defined
- => only conduction charges are sources & sinks of D fields
- conduction & polarisation charges are sources & sinks of E fields

Define magnetisation
-
M = m/V
- magnetic moment m per unit volume
- direction of average B field produced by many magnetic dipoles Bm is in the same direction as M (they are parallel unlike with electric dipoles and their average E field)
- torque tends to align m with external B field

Define the H field (magnetic intensity)
- H arises from free currents (measured by ammeter)
- M arises from bound currents associated with magnetic moments due to angular momentum of e-s at QM level

Deriving expression for transformer.
emf generated in primary coil - Ep = - Np * Flux B
Es = - Ns* Flux B
Since the flux through each coil is the same, equate the fluxes to get - Ep = (Np/Ns)*Es
Explain briefly why electricity is transported around the UK via high voltage transmission lines rather than low voltage, and alternating current rather than direct current.
- Power transmission is given by P=IV
- therefore, to maximise the power transmitted, higher voltages should be used
- power loss from voltage drops due to wire resistance is given by Ploss=I2R
- to minimise power loss, small currents and wires of low resistance should be used
- Also, Ploss= V2/R, where V is the voltage drop across the lines
- maximise transmitted P => reduce P loss (voltage drop minimised)
- AC voltages are more readily transformed by utilising Faraday’s Law in Step-Up transformers
- raises the voltage so that maximum power is transmitted
State equation for electrostatic potential energy of a system of N charges.

What are the units of magnetic moment μ?
Am2
Keywords associated with magnetic force
- FB always perp. to v
- |v| = constant since KE = constant
- v = vperp + vparallel
- vperp = circular motion at cyclotron frequency
- vparallel = unchanged
- v = vperp + vparallel
- centripetal force = FB
Mass spectrometer
- only v =E/B will pass through velocity selector (which has both E & B fields)
- apply 2nd uniform B field (no E field)
- trajectory of particle is circular
- centripetal force = magnetic force
- obtain m/q
LCR circuit phasor diagrams; current & instantaneous voltage amplitude and phase
- current has same amplitude and phase in circuit

Gauss’s law for dielectrics

Electric dipole potential derivation
- cosine rule for both
- then binomial expansion

Maxwell eqns in integral and differential form

Maxwell equations for matter



