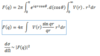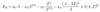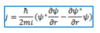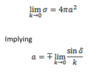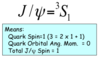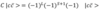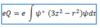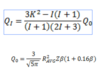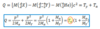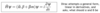Nuclear & Particle Physics

Question 1

How are orders determined in Feynman diagrams?

Question 2

What are the quark compositions of the lightest known mesons, the pions (0, +, -)?

Answer 2

Question 3

What are the quark compositions of the lightest strange mesons, the kaons (+, 0)?

Answer 3

Question 4

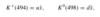
What are the rules of Feynman diagrams?

Question 5

What is the overall effective coupling?

Question 6

Why does the charged pion have longer lifetime than a meson in an excited state?

Question 7

Why are some decays observed but not others?

Question 8

What changes do you make to work in natural units?

Question 9

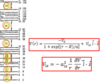
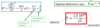
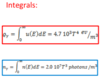
What is the scattering amplitude for the Yukawa potential?

Question 10

What is the Yukawa potential?

Question 11

How do you calculate the radius of scission?

Answer 11

• r = R₀ A^1/3

Question 12

What is the centrifugal potential? When is it included?

Question 13

How does the Q value change if centrifugal was accounted for in the potential?

Question 14

What are the conservation laws involved in nuclear reactions?

Answer 14

*

Question 15

What is the total energy of a particle?

Question 16

What is the Lorentz factor? How would distance change in relativistic kinematics compared to non-relativistic kinematics?

Question 17

What makes something a strong interaction?

Question 18

What are the conservation laws for weak interactions?

Question 19

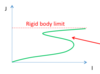
What is the liquid drop model for atomic nuclei?

Question 20

What are the ordinary particles?

Answer 20

• electrons (electricity and chemical reactions)
• electron neutrino (billions pass through body all the time)
• up quark (+2/3 e)
• down quark (-1/3 e)

Question 21

What are force particles? And what are they? Which kind of particles experience them?

Answer 21

• transmit 4 fundamental forces of nature
  
  • gluons; strong => quarks
    
    • explosive release of nuclear E
  • photons; EM => quarks & charged leptons
    
    • electricity, magnetism & chemistry
  • (intermediate vector) bosons; weak => quarks & leptons
    
    • W- W+ Z0
    • some forms of radioactivity
  • gravitons; gravity => all particles with mass
    
    • all weight experienced is due to gravitational force

Question 22

What is elastic scattering?

Answer 22

• only change in direction of momentum (not magnitude)
• i.e. magnitude of momentum before and that of after are the same

Question 23

What is alpha particle scattering?

Answer 23

• size of nucleus

Question 24

What is electron scattering?

Answer 24

• charge distribution (protons) inside nuclei

Question 25

What is deep inelastic collisions?

Answer 25

• Quarks inside nucleons

Question 26

What is ultrarelativistic electron-nucleus collisions?

Answer 26

• glue inside nucleons and nuclei

Question 27

What is (reaction) cross section?

Answer 27

• defined from reaction rate
  
  • which is R_b = I_aNσ (what’s N and Ia?)
• σ = cross section = R_b/I_aN
• effective area that quantifies the intrinsic likelihood of a scattering event when an incident beam strikes a target object, made of discrete particles
• measured in units of area; most commonly a barn

Question 28

What is 1 barn?

Answer 28

• 1 barn = 10^-28 m² = 100 fm²

Question 29

What is the differential cross section?

Answer 29

• quantifies the intrinsic ratte at which scatteed projectiles can be detected at a given angle
  
  • dσ/dΩ is not a differential, just a symbol
• rate into a solid angle element is
  
  • dR_b = r(θ, φ) dΩ/4π
    
    • θ is the scattering angle measured between incident beam and scattered beam
    • φ is the azimuthal angle (usually scattering processes have azimuthal symmetry and therefore do not depend on φ)
• differential cross section is:
  
  • dσ/dΩ = (dR_b/I_aN) r(θ, φ)/4π = r(θ, φ)/I_aN4π

Question 30

What is the impact parameter, distance of closest approach and scattering angle in Rutherford scattering?

Question 31

How do you determine the Rutherford cross section?

Answer 31

• conservation of momentum, energy (elastic scattering) and angular mom.
• relationship between scattering angle and impact parameter
  
  • b = d/2 cot(Θ/2)
    
    • b = impact parameter
    • d = distance of closest approach
    • Θ = scattering angle
• scattering cross section
  
  • dσ/dΩ = (zZe²/4πε₀)(1/T_a)² 1/sin⁴(Θ/2)
  • (what’s Ta?) (+ are we supposed to know this eqn?)
• magnitude of change of momentum
  
  • |Δp| = |ћq| = 2mћv₀sin(Θ/2)
• Rutherford cross section is
  
  • dσ/dΩ ~ 1/q⁴
• (What is the point of knowing this?)

Question 32

What is Fermi’s Golden Rule?

Answer 32

• probability for transition between initial state and final state
  
  • λ = 2π/ћ ρ(E_f) |V_fi|² (what’s the point of 2π here?)
    
    • V_fi is the matrix element:
    • V_fi = integral of ψ_f*Vψ_i dv (volume integral?)
  • particle are plane waves
    
    • hence ψ_{<span>i</span>} = e^{-i<strong>k_i.r</strong>} = e^{-i<strong>p_i</strong>/ћ<strong>r</strong>}
• scattering transition probability is
  
  • |V_fi|² ~ |F|² where F is the form factor?

Question 33

How is the form factor derived?

Answer 33

• V_fi = F = integral of e^{i(<strong>p_f</strong>/ћ)r} V e^{-i(<strong>p_i</strong>/ћ)r} dv
  
  • q defined as |Δp|/ћ
• hence F(q) = integral of e^{i<strong>q</strong>r} V dv
• in spherical coordinates
  
  • F(q) = integral of e^iqrcosθ V r² dr sinθ dθ dφ
  • =

Question 34

How is the nuclear charge density probed? And how is it obtained?

Answer 34

• e- scattered inside a +vely charged nucleus probes its interior
• obtained by
  
  • measuring cross section vs scattering angle
  • deduce form factor
  • obtain charge density of nuclei

Question 35

What is the equation of nuclear radius and volume? Why is it called the liquid drop model for atomic nuclei?

Answer 35

• nuclear radius
  
  • r = r₀ A^1/3
    
    • r₀ = 1.25 fm
• hence nuclear volume
  
  • V = r₀³ A
• since nuclear size scales with number of constituents
  
  • like a drop of liquid

Question 36

How else can nuclear radius be determined?

Answer 36

• from atomic transitions (point charge or uniformly charged sphere) - don’t really know what this means
  
  • particularly for 1s where e- is inside nucleus
    
    • get isotope shifts

Question 37

What are muonic atoms? And why may they be better at determining the size of the nucleus?

Answer 37

• where muon replaces e-
• have smaller Bohr radius
  
  • hence greater sensitivity to size of nucleus

Question 38

What reflects the differences in nuclear size and distance between the protons?

Answer 38

• Coulomb energy differences between mirror nuclei (e.g. 13-N(7,6) and 13-C(6,7))
• is there more to say about this?

Question 39

When does the Rutherford scattering formula breakdown?

Answer 39

• at short distances (higher energy) when incident α particle gets close enough to target nucleus that they interact via the nuclear force
  
  • (in addition to the Coulomb force that acts when they are far apart)
  • => projectile hits surface
• point at which the formula breaks down gives a measure of the size of the nucleus

Question 40

When does nuclear scattering effects appear? What Bohr radius does this correspond to? And how does this compare to the meanr Bohr radius?

Answer 40

• at separations of less than 12.15 fm
• corresponds to R₀ = 1.7 fm
  
  • greater than mean radius of 1.25 fm
  • but consistent with “skin thickness” of about 0.5 fm
  • which allows 2 nuclear distributions to overlap at these larger distances

Question 41

What is the definition of amu (atomic mass units)? And what is its equivalence in other units?

Answer 41

• 1 amu = 1/12 of mass of ¹²C
• 1 amu = 931.5 MeV = 1.66 10-²⁷ kg

Question 42

What is binding energy? And when is it positive?

Answer 42

• B = Δmc²
  
  • where Δm = Zm_p + Nm_n - mx
    
    • Z = atomic number; m_p = mass of proton in amu
    • N = number of neutrons; m_n = mass of neutron in amu
    • m_x = mass of the particle in amu
• binding energy for stable systems is +ve
  
  • assembled systems weighs less than sum of constituents

Question 43

What does the graph for binding energy per nucleon B/A vs mass number A look like? Which are the stable elements?

Answer 43

Question 44

What is the semiempirical mass formula (based on liquid drop assumption) using binding energy? And what are the correction terms?

Answer 44

• volume (bulk)
  
  • a_v A => a_v = 15.5 MeV
• surface reduces binding (based on strong force; surface tension in liquids)
  
  • a_s A^2/3 => a_s =1 6.8 MeV
• Coulomb repulsion between protons
  
  • a_c Z(Z-1)/A^1/3 => a_c = 0.72 MeV
• (A)symmetry energy (imbalance of no. of protons and neutrons for a given number of nucleons; Pauli exclusion principle)
  
  • a_A (A-2Z)²/A => a_A = 23 MeV
• Pairing correction (spin coupling effects)
  
  • δ(A,Z)
    
    • = +δ₀; Z, N even (A even)
    • = 0; A odd
    • = -δ₀; Z, N odd (A even)
      
      • δ₀ = a_p/A^1/2

Question 45

What are the contributions of various terms in the semiempirical mass formula to the binding energy per nucleon? Which term reduces binding energy for light nuclei and which term reduces binding for heavy nuclei? What is the most superheavy nuclei recorded?

Answer 45

• surface reduces binding for light nuclei
• Coulomb reduces binding for heavy nuclei
  
  • Nuclear shell structure affects structure significantly
• Upper limit in isotope chart set by fission
• Superheavy nuclei has Z = 119

Question 46

What is the most stable isotope from the mass formula?

Mass formula = M(A,Z) = Zm_p + Nm_n - B(A,Z)/c²

How can nuclei be brought towards valley of stability?

Answer 46

• dM/dZ = 0
• by beta decays
  
  • beta- = n -> p + e^- + anti-v (hence for lower Z)
  • beta+ = p -> n + e⁺ + v (hence for higher Z)

Question 47

What is quark gluon plasma?

Answer 47

• existed in the universe at t < 10^-5 - 10^-9 sec
  
  • what’s t?
• in the past
• now the world is composed of hadrons
• can it be recreated on Earth?

Question 48

What is the density like in the early universe?

Answer 48

• no net density
  
  • => about equal amounts of matter and antimatter

Question 49

How do you recreate the early universe?

Answer 49

• temperature predicted by theory (LQCD) is ~ 10¹²K ≈ 1000 billion degrees
  
  • obtainable by LHC (T = 250 MeV); RHIC (T = 180 MeV)
    
    • not really sure what the figure is showing? too much going on

Question 50

What are the symmetry principles SU(3) x SU (2) x U(1)?

Answer 50

• need symmetry breaking to give mass
• Higgs boson is evidence of Brout-Englert-Higgs symmetry breaking mechanism (1964)

Question 51

What is the Lagrangian and its relation to principle of least action?

Answer 51

• Lagrangian: L = T-V
  
  • allows to determine equations of motion by sub. into Euler-Lagrange eqn
• Principle of least action:
  
  • area under L vs t is the action
    
    • physical paths minimise the action

Question 52

What are hadrons? List the composition of the common types with their charge, mass and spin.

Answer 52

• baryons and mesons
  
  • baryons qqq or antibaryons q-q-q- (fermionic hadrons)
  • mesons qq- (bosonic hadrons)

Question 53

What suggested a new quantum number (colour)?

Answer 53

• existence of Δ++ = uuu
• to respect Pauli Principle
  
  • 3 values of colour (RGB - just representatives)

Question 54

What is the mass of a proton, mass of a neutron, mass of a pion, mass of an electron, ћc, fm/c? Masses are in MeV according to E=mc²

Answer 54

• M_p ≈ 938 MeV
• M_n ≈ 939 MeV
  
  • ≈ 1 GeV
• M_π = 140 MeV
• M_e = 0.511 MeV
• ћc = 197.32 MeVfm
• fm/c = 0.3*10^-23 sec

Question 55

What are the conservation laws in reactions?

Answer 55

• lepton number, charge, baryon number, CPT are conserved in all interactions
• flavor and parity conserved in strong & EM, broken by weak
• isospin conserved by strong, broken by EM (except I_z)

Question 56

Which symmetry group are gluons described by? And how many combinations of linearly indt gluons are there? List them.

Answer 56

• SU(3) describing color and anticolor (R- = cyan, G- = magneta, B- = yellow)
• g0 does not change colour hence only 8
  
  • don’t get why g7 or g8?

Question 57

What are the differences between QED and QCD in terms of interaction and screening?

Answer 57

• QED: photon has no charge hence no self interaction
  
  • at large distances, charge is screened => α = 1/137
  • small distances, α increases (since more charge seen)
• QCD: gluon has colour charge => self-interaction (split and fuse)
  
  • at smaller distances (because of the gluon cloud), α_s decreases so less colour charge seen => antiscreening
  • gives rise to asymptotic freedom

Question 58

What is asymptotic freedom?

Answer 58

• quark-quark potential vs distance (r)
  
  • at large distances, α_s increases => energy becomes infinite
  • no free quarks possible so always q and q- pairs
    
    • => confinement

Question 59

What is the simple model of phase transitions of quark matter?

Answer 59

• like water: T_HG = T_QGP, P_HG = P_QGP, μ_HG = μ_QGP
• where P_HG = P_baryons + P_mesons ≈ P_mesons
  
  • P_HG ≈ P_π = g_π(π²/90)T⁴ ≈ 3(π²/90)T⁴ (g_π ≈ 3)
• where P_QGP = P_quarks + P_gluons - B
  
  • P_QGP = (g_q + g_g)(π²/90)T⁴ - B ≈ 40(π²/90)T⁴ - B
  • MIT ‘Bag Model’ estimates Bag Constant, B ≈ 10²³ atm
• from eqns for P, critical phase temp can be found
  
  • T(crit) ≈ 150 MeV
  • lattice QCD predicts T(crit) ≈ 175 MeV
    
    • E = kT => T ≈ 10¹² K

Question 60

What are the equations useful for relativistic kinematics?

Answer 60

• e.g. at RHIC, proton with E = 100 GeV => γ = 100 GeV
  
  • at LHC, proton with E = 2750 to 7000 GeV => γ = 2750 to 7000

Question 61

How can you calculate energy etc. in lab and CM frame using relativistic kinematics?

Answer 61

• set c = 1
  
  • then E² - p² = m² which equals an invariant quantity, let’s say s => E² - p² = m² ≡ s
• e.g. for any system of 2 particles with (E₁, p₁) and (E₂, p₂)
• s ≡ (E₁ + E₂)² - (p₁ + p₂)²
  
  • s = E₁² + E₂² + 2E₁E₂ - p₁² - p₂² - 2p₁.p₂
  • s = m₁² + m₂² + 2E₁E₂ - 2p₁.p₂
• 1) target at rest in lab frame: p2 = 0 hence E₂ = m₂
  
  • s = m₁ + m₂ + 2E₁m₂ ≈ 2E₁m₂
• 2) collider in CM frame (CM frame so p=0 => p₁=-p₂)
  
  • s = (E₁ + E₂)² - (p₁ + p₂)² = (2E)²
  • sqrt(s) = 2E

Question 62

What is the difference between tranverse variables and longitudinal varibles? What is pseudorapidity?

Answer 62

• tranverse variables are Lorentz invariant
  
  • p_t = sqrt(p_x² + p_y² ) [tranverse momentum]
  • m_t = sqrt (p_t² + m² ) [transverse mass]
• longitudinal variables: rapidity is additive under Lorentz transformations from one frame of reference to another
  
  • y = 1/2 ln(E + p_z/E - p_z)
  • y = 1/2 ln(1 + βcosθ/1 - βcosθ)
    
    • β ≈ 0 => y ≈ β; β ≈ 1 => y ≈1/2 ln(2/1-β)
    • θ = 90 => y = 0 (midrapidity); θ = 0, y -> infinity
• E = m_t cosh y
• pseudorapidity
  
  • η = ln cot(θ/2)

Question 63

Why is the strong force between nucleons not mediated by gluon exchanged?

Answer 63

• because of colour confinement
  
  • thus gluons have colour and are not ‘allowed’ to move outside the nucleon

Question 64

What is the Yukawa potential?

Answer 64

• screened Coulomb potential
• nucleon-nucleon interaction is due to exchange of massie quanta (e.g. pions +,-, neutral) [not sure how this links in to what it is]
• also is the eqn correct? One on wikipedia for classical potential of 2 fermions ineracting through a Yukawa potential is similar but g²
• R = range of interaction
  
  • from uncertainty relation ΔEΔt ≈ ћ => mc²(R/c) ≈ ћ
  • R ≈ ћ/mc = ћc/mc²≈ 197.32/140 ≈ 1.5 fm
    
    • multiply by c/c to use ћc = 197.32

Question 65

What is a pseudoscalar? How does a vector meson differ from pseudoscalar?

Answer 65

• pseudoscalar is a scalar with spin 0 but flips signs under parity transformation
• pseudoscalar meson
  
  • e.g. pion (m = 140 MeV); J^P = 0
• a vector meson has spin 1 and -ve parity (J^P = 1-)
  
  • e.g. rho (m = 770 MeV)
  • omega (m = 782 MeV)
• meson exchange underlies the nucleon-nucleon interaction

Question 66

How does the form factor for the Coulomb potential differ from the Yukawa potential?

Answer 66

• Coulomb: form factor for extended density distribution (nuclei)
  
  • constant density => oscillating form factor
  • infinite range
• Yukawa: form factor for potential mediated by heavy virtual particle

Question 67

What is the intrinsic parity of particle and of antiparticle?

Answer 67

• of particle = +1
• of antiparticle = -1
• parity: P = (-1)^L+1
• C-parity: |qq_bar> = C |q_barq>
• J^PC

Question 68

What is the deuteron?

Answer 68

• simplest bound nucleus
  
  • A=2, Z=1, hydrogen
• only one bound state with E = -2.225 MeV
• I^π = 1+ (what is this?)
• R_ch = 2.14 fm (what is this?)
• spin of neutron and proton = 1/2 each
  
  • I = 1

Question 69

What is the magnetic moment of the e- and nucleon?

Answer 69

• μ = AI
  
  • A = πr²
  • I = q/t
• t = 2πr/v = 2πr/(p/m) [p=mv]
• μ = qћl/2m
  
  • e-: μ = -eћl/2m_e ≡ -μ_Bl
  • nucleon: μ = eћl/2m_N ≡ μ_Nl
• => μ ≡ g_llμ_B or μ ≡ g_llμ_N (g is the g-factor)
  
  • orbital e-: μ_l ≡ g_llμ_B; g_l = 1
  • spin of e-: μs ≡ -gsμ_Bs; gs = 2
• expect g_s(p) = 2 & g_s(n) = 0 but in experiments, g_s(p) = 5.5856 & g_s(n) = -3.8261
  
  • => nucleon has a substructure => quarks

Question 70

What does the magnetic moment of deuteron suggest? What do the quantum numbers suggest about the spin state of the deuteron?

Answer 70

• indicates proton and neutron spin are parallel
  
  • S = 1/2 + 1/2 = 1
  • difficult to start from fundamental interaction => try effective model approach
• quantum numbers
  
  • L= 0
    
    • π = (-1)^L = +1 (parity)
  • I = 1
    
    • I_z = -1, 0, +1 => deuteron is in TRIPLET state
  • => nucleon-nucleon interaction must be spin dependent (no singlet state exists)

Question 71

What is the depth of nuclear potential?

Answer 71

• V₀ = 35 MeV (solved numerically & to first order)
  
  • by modelling the binding of the deuteron in a square well potential
  • an attractive central potential

Question 72

How can neutron-proton free scattering be treated? What is the angular momentum in neutron-proton free scattering?

Answer 72

• same way as bound problem of deutron but with E > 0
• L = mvb
  
  • in QM: lћ = mvb
  • l = 0: l = mvb/ћ << 1
• p = mv = sqrt(2mE) => E << ћ²/2mb² ≈ 20 MeV
  
  • b = impact parameter
• if neutron has low energy (E = keV or few MeV) then scattering is s-wave (l=0)

Question 73

What is the effect of a scattering potential?

Answer 73

• to shift the phase of the scattered wave at points beyond the scattering regions, where the wave fn is that of a free particle
• phase shift changes sign at high projectile energy
  
  • change in s-wave phase shift from +ve to -ve at about 300 MeV
    
    • => at these enegies, the incident nucleon is probing a repulsive core in the nucleon-nucleon interaction
  • repulsive at short distances
  • attractive in the well?

Question 74

What are currents in relation to wavefn? How can currents be used to calculate the scattering cross section (scattering probability) into an element of solid angle?

Answer 74

• number of particles per second
• dσ = current into solid angle element dΩ/incident current = j_scattered r² dΩ/ j_incident
• the differential cross section (cross section per unit solid angle) is dσ/dΩ = (sinδ)²/k²
• and total cross section (L=0) integrated over all angles is
  
  • σ = 4π (sinδ)²/k²

Question 75

Why is the deuteron triplet potential calculated (σ = 4.6 barn) so different to the experimental value (σ = 20 barn)?

Answer 75

• because nucleon-nucleon interaction is spin dependent

Question 76

What is the scattering length?

Answer 76

• not a length (unit is length though) but represents the strength of the interaction
  
  • bound state has +ve scattering length whereas an unbound has -ve

Question 77

What is shell structure of the atom?

Answer 77

• central Coulomb potential: e-s experience attractive field of nucleus
• atoms with many e-s => Hartree Fock approximation (effective charge)
• atomic radius (nm) & ionisation energy (eV) vs Z shows smooth variations which correspond to gradual filing of an atomic shell
  
  • sudden jumps show transitions to the next shell

Question 78

What are the magic numbers?

Answer 78

• particular stabilities at particle numbers 2, 8, 20, 28, 50, 82, 126
  
  • suggests that atomic nucleus has a shell structure like the atom
  • => try to solve using central potential (though nuclear density profile suggests this will not work)

Question 79

How can energy levels be obtained? Which central potentials V should be used?

Answer 79

• Schrodinger eqn
  
  • wavefns are antisymmetric for fermionic systems
  • radial eqn
• use infinite deep well & harmonic oscillator
  
  • which works OK for lowest states but not for higher states
  • large gaps occur between energy levels which are associated with closed shells

Question 80

What is the Woods-Saxon potential? What are the nuclear levels like from W-S potential?

Answer 80

• since nucleon density is constant in nuclear interior (for r < R) => can try potential with flat central part
• state with angular mom. l has (2l+1) magnetic substates
  
  • m_l = -l, .., 0, …, +1
  • 2 spin states (-1/2, +1/2)
• level degeneracy is 2(2l+1)
• 1p tate is first state with l=1

Question 81

What is spin-orbit coupling? And its importance in atoms?

Answer 81

• s.l term is important in nucleon-nucleon interaction
  
  • add V∝ l.s to W-S potential
• calculate expectation value of V∝ l.s (spin orbit potential):
  
  • ΔE = energy difference between l states when they split up
• spin orbit in nuclei has opposite sign(-) compared to atoms(+)
  
  • which sign are you talking about?
• if l & s are no longer good quantum numbers => j = l+s is a good QN

Question 82

What is the effect of spin orbit potential Vl_s and Woods Saxon potential?

Answer 82

• reproduces magic numbers
• level degeneracy is 2j+1

Question 83

What is hadron spectroscopy? What is the Charmonium potential?

Answer 83

Question 84

What does J^PC mean?

Follow on from spectroscopic notation of J/ψ.

Answer 84

Question 85

What is C-parity?

Answer 85

• particle ⇔ antiparticle

Question 86

What are the symmetry operations in conversation laws?

Answer 86

• P (Parity): inversion of spatial coordinates (does not change spin and angular mom.)
• C (Charge conjugation): inversion of all intrinsic QN (changes charge, lepton, baryon, strangeness etc. numbers)
  
  • C is Unitary (C² = 1) and Hermitian (C = C⁺)
  • C|ψ>= η_c|ψ> [what’s η_c?]
  • strong and EM obey C symmetry; weak violates
  • e.g. neutrinos are left-handed & antineutrinos are right handed
• T (Time): inversion of all derivatives e.g. mom. and angular mom. (leaves F=ma unchanged => forces are conserved)
• CPT invariance absolutely true (Lorentz invariance => CPT invariance)
  
  • integer spin particles follow BE stats, 1/2 integer ones follow FD stats
  • q and q_bar have identical mases and lifetimes
  • q_bar has opposite QN of q
• CP approximately conserved but partially broken in weak
  
  • e.g. the Kaon decays not equally prob. under CP
    
    • K₀^L -> π+ + e- + anti-v_e
    • K₀^L -> π- + e⁺ + v_e

Question 87

What is the reason for δ in semi-empirical mass formula? What does this suggest about the ground state of even-even nuclei & odd-even nuclei, and excited states in odd-even nuclei?

Answer 87

• short range attractive nucleon-nucleon interaction bind nucleons into paris moving in time reverse orbits with m_j=-j and m_j=+j (magnetic moments; right hand rule)
• even-even nuclei ground states: I^π = 0+
• odd-even nuclei ground states: filled proton shells do not contribute to structure
  
  • properties of ground state determined primarily by odd neutron => total spin and parity determined by valence nucleon or hole
• excited states in odd-even nuclei: (don’t know what the figure is showing?)

Question 88

Why does the Shell Model work? Where does it fail?

Answer 88

• energy of nucleons can to good approximation be calculated from an effective central potential + spin-orbit coupling
• energy levels show shell structure
• magic numbers are understood
• nucleons move indtly in this potential, unaffacted by others (extreme indt particle model)
• works because Pauli blocking prevents nucleons inside the nucleus to scatter on each other (which would otherwise destroy the regular motion)
  
  • scatterings only allowed if final states are outside Fermi sphere |p’_i| > |p_F|; |p’| > |p_F|

Question 89

How much energy does it cost to break a pair of nucleons in the expected Shell Model states? Which state is unexpected from the Shell Model?

Answer 89

• costs ≈ 2 MeV to break a pair
• 2+ unexpected
• 130-Sn

Question 90

What are the 2+ states below E = 2 MeV?

Answer 90

• new states corresponding to other excitations of the nucleus
  
  • not ‘shell model states’

Question 91

What are collective excitations?

Answer 91

• involve all nucleus coherent motion
  
  • indt particle motion (single particle motion) => weak gamma transition; spherical shape
  • whereas correlated particle motion (collective rotation, vibration) => strong gamma transition; rugby football or pancake shape

Question 92

What can be suggested about the states if the vibration is harmonic?

Answer 92

• states are equidistant (compare Harmonic oscillator)
• above 2 MeV, structure becomes complicated and no vibrational patterns can be seen

Question 93

What are the dipole and quadrupole vibrations characteristic?

Answer 93

• vibrational quanta = phonons
• dipole vibrations are shifts of CM: not allowed in absence of external forces
• quadrupole vibration (λ = 2) is the lowest occuring mode
  
  • λ=2 phonon assigned parity (-1)^λ​=+1 since it creates a shape with reflection symmetry ψ(-r)=ψ(r)
  • an even-even nucleus in GS has I^π = 0+
  • => adding a λ=2 phonon create the first excited state I^π = 2+
• adding 2 λ=2 phonons gives the following possible states: 0+, 2+, 4+
  
  • only total λ=λ1+λ2 values with μ=μ1+μ2 values from -λ to +λ are allowed
• adding 3 λ=2 phonons gives possible states 0+, 2+, 3+, 4+, 6+

Question 94

How do you characterise the shape of a charge distribution?

Answer 94

• using the quadrupole moment
  
  • spherical => Q = 0
  • prolate => Q > 0
  • oblate => Q < 0

Question 95

How is the intrinsic quadrupole moment Q₀ related to the deformation β? What is β of ground state of the many nuclei in the ‘rare earth’ region e.g. Dy, Er, Yb, Hf etc.? What else does a deformed nuclei suggest?

Answer 95

• β ≈ 0.3
• they might be able to rotate

Question 96

How are rotating nuclei formed?

Answer 96

• fusion-evaporation heavy ion fusion reactions
  
  • beam nucleus hits target nucleus -> fusion 10^-22 s ->
  • either fast fission
  • or compond formation 10-¹⁹ s; ~0.75 MeV; ~ 2*10²⁰ Hz -> rotation -> cooling 10^-15 s -> ground state 10^-9 s
• p₁ = m₁v₁; p₂ = 0
  
  • p_rec = m₁v₁;= (m₁+m₂)v_rec
• E_cm = 1/2(m₁+m2)v_rec²
  
  • E₁-E_cm=E* (what’s E*)
• rotation increases with angular mom. and excitation energy
  
  • excited states can emit a photon to reduce rotation

Question 97

What is the rotational energy (which gives rise to the spectrum of rotational states)? When is there reflection symmetry?

Answer 97

• reflection symmetry ψ(-r) = ψ(r)
  
  • only states with +ve parity allowed
  • only even values of rotational angular momentum
• from E vs I, can obtain moment of inertia J
  
  • e.g. get E in terms of 2+, 4+, 6+
  • plot E vs I; curve goes through the points

Question 98

What does a graph of J vs I look like? How does the Coriolis force relate?

Answer 98

• backbend is the breaking of a pair of nucleons due to the Coriolis force F_cor = 2mv×ω
• Coriols force in a rotating nucleus can break a pair of nucleons moving in time reversed orbits
  
  • and align the single particle angular momenta along rotation axis
  • so +m_j and -m_j (+j and -j) becomes +j and +j

Question 99

How does the measured quadrupole moment Q_I of a rotating nucleus relate to the intrinsic quadrupole moment Q₀?

Answer 99

Question 100

What is the Nilsson shell model for deformed nuclei? How does deformation affect good quantum numbers? How are single nucleon states labelled by? What is an approximately good QN for deformed nuclei? What are the Nilsson states?

Answer 100

• uses a 3D deformed harmonic oscillator potential with axial symmetry, spin orbit and I² terms
  
  • then solve Schrodinger eqn to get nuclear energy levels
• deformation means J=l+s is no longer a good QN => degeneracy of J states lifted
• label single nucleon states by
  
  • N = n₃ + n_⊥
  • Λ = component of I on symmetry axis
  • Ω = component of j on symmetry axis
• f_7/2? => j=7/2; lowest energy (lies closest and will interact most strongly with the core)
• Nilsson states: shell closures (magic numbers) for spherical nuclei (86 and 116, 82 and 126)
  
  • predict large deformation for N=86, e.g. nucleus 152-Dy

Question 101

What is superdeformation? What is the energy difference between the levels?

Answer 101

• gamma-rray of superdeformed band in 152-Dy (looks like a peanut)
• different decay sequences (‘bands’) each correspond to a given shape => several shapes ‘coexist’ in the nucleus
  
  • prolate γ=0º, β=0.2; oblate γ=60º, β=-0.1; prolate superdeformed γ=0º, β=0.6 (angular momentum close to fission limit; excitation energy above GS)
• superdeformed nuclei are exotic

Question 102

What are superheavy nuclei (SHE)? Where is the predicted island of stability? What is a nuclei far from stability?

Answer 102

• possibility of shell gaps at high N and Z numbers N=104 to N=118
• predicted island of stability at Z ≈ 110-120 and N ≈ 175-185
  
  • Z = 109-118
  • Z= 108 (Hassium) is longest lived isotope? => probably more stable can be found
    
    • Z = 115 recently announced (2013)
• halo nuclei (weakly bound neutrons = > neutron halo)
• both superheavy and halo nuclei are exotic nuclei

Question 103

What can be said about the nuclei in terms of vibration and rotation?

Answer 103

• they can vibrate
  
  • lowest excitation is quadrupole vibration
  • states are equidistant
• they have static deformations
• they can rotate
  
  • energy states increases quadratically with angular mom.
  • moment of inertia can be measured from energies and sequence of gamma rays

Question 104

What is the Q-value in α radioactivity? And what do masses and Q-value determine? What is the range of Q-values for heavy nuclei?

Answer 104

• masses and Q-value uniquely determine α energy
• Q = (3-10) MeV
  
  • Z = 82 shell
  • N = 126 shell

Question 105

What is the Coulomb energy for alpha decay?

Answer 105

Question 106

Calculate the Coulomb energy and Q value for this alpha decay.

Answer 106

• Coulomb energy and Q value in MeV are at r=R in an potential barrier?
  
  • square well then exponential decay in V vs r

Question 107

What is the barrier penetration model (tunneling through potential barrier) for alpha decay? Where is alpha decay is more probable? Alpha decay is a QM phenomenon; reduced probability but not reduced energy after barrier.

Answer 107

• λ = 1/Ta = P(formation)*Frequency(knocking)*P(barrier penetration)
• probability to preform an α inside nucleus ≈ 0.01 -> (nucleons near Fermi surface have similar momenta)
• frequency of ‘knocks’ at barrier
  
  • t = R/v = 8/0.25c = 10^-22 s
  • v = 1/t ≈ 10²² s-1
• probability of barrier penetration
  
  • P= e^-2G where G = Gamow factor
  • exponential dependence of Gamow factor explains large variation in α-halflife as a consequence of variation of Q value relative to Coulomb barrier height
• more probably at tips of a deformed nucleus (lower and thinner barrier)

Question 108

How to estimate the age of the Earth?

Answer 108

• from relative abundance and half-life of
  
  • 235-U (0.72%; t₁ = 7.04*10⁸ yrs)
  • and 238-U (99.27%; t₂ = 4.47*10⁹ yrs)
• N₁(t) = N₀₁e-^t/t₁
• if N₀(235-U) = N₀(238-U) => t = 5.9*10⁹ yrs
• if N₀(235-U) = 0.1N₀(238-U) => t = 3.14*10⁹ yrs
• compare nuclear synthesis models and Supernova models

Question 109

What are the assumptions made in 14-carbon dating? How to calculate time elapsed since absorption with uncertainty if in 64 g of C, 2 Bq (decays/sec) were measured?

Answer 109

• 14C prodn is constant over time
• 14C absorption by living organisms is constant in time
• 14C decay rate is constant (1 Bq per 4 g of C in ‘fresh’ organic matter)
• expect 64/4 = 16 Bq
  
  • so sample has decayed by a factor 2/16 = 1/8 = 1/2³
  • => time elapsed since absorption is 3*5730 yrs = 17200 yrs
• uncertainty on sample with N counts is sqrt(N)/N = 1/sqrt(N)
• if 1% accuracy (Δt = 172 yrs) desire => need 10,000 counts = > measure 5000 s for 64 g
  
  • if only 64 mg available => must measure for 5000*1000 = 5*10⁶ sec ≈ 58 days
  • so backgound radiation becomes important => shield

Question 110

What is beta decay? What is electron capture and neutrino capture? What is the helicity of antineutrino and neutrino? What is the underlying process in beta radioactivity?

Answer 110

• β- (n->p+e-+antiv_e), β+ (p->n+e++v_e), e- capture(e-+p->n+v_e)
  
  • NB: free proton does not decay (p is lightest baryon) but is possible in nuclei if Q value > 0
  • continuous e- distribution from β decay until end point T_e = Q => 3 body decay => existence of neutrino
• m_n-m_p = 1.3 MeV => free neutron decays with t_1/2 = 10.5 mn
• neutrino capture
  
  • anti-v_e + p -> n + e+
  • v_e + n -> p + e-
• helicity of anti-v_e = +1 (right handed)
• heclicity of v_e = -1 (left handed)
• weak decay of quarks; weak interation mediate by W and Z bosons
  
  • involves matrix elements between initial and final nuclear states

Question 111

What is Fermi’s theory for beta decay?

Answer 111

• Fermi’s Golden Rule
• ρ(E_f) = density of final states = dn/dE_f
• |V_fi|² = Matrix element
• plane wave approximation for e and v (what’s v?)

Question 112

How do you calculate e- spectrum from Fermi’s theory for beta decay?

Answer 112

• E_f = E_e + E_v = E_e + qc
  
  • dq/dE_f = 1/c at fixed E_e
• N(p) dp = C p2q2 dp
  
  • because N(p=0) =0 and for T_e=Q from figures of expected e- energy and momentum distributions

Question 113

What is F(Z’,p) in total beta decay rate? And what is the total beta decay rate for λ=ln2/t_1/2? What are superallowed decays? Why is log₁₀(ft) plotted?

Answer 113

• F(Z’,p) is Fermi fn which represents the Coulomb interaction between the daughter nucleus and the e-
  
  • Fermi integral is dimensionless
• superallowed decays have shortest half-lives of log(ft) = 3-4
• log₁₀(ft) plotted due to large spread in half-lives
• for 0+ -> 0+: M_fi = √2 => g = 0.88*10^-4 MeV fm3 (corresponds to the below for weak)
  
  • strong: 1
  • EM: 10^-2
  • Weak: 10^-5
  • Gravity: 10^-39

Question 114

Why are the momentum and KE spectra of e-s and e+s emitted in beta decay different?

Answer 114

• differences arrise from Coulomb interactions with daughter nucleus
  
  • e-: attraction
  • e+: repulsion

Question 115

What is the end point of the spectrum sensitive to?

Answer 115

• neutrino mass
• c²p dp = (T_e + m_ec²) dT_e
• dN/dp =
  
  • -> 0 if mv = 0
  • -> ∞ if mv > 0
    
    • at endpoint

Question 116

When might a neutrinoless double beta decay (0vββ) occur? Why might this not happen?

Answer 116

• if neutrino and antineutrino were identical particles
• but different helicity of neutrino and antineutrino suggest that they are different
• Majorana particle (suggests that the neutrino is its own antiparticle)
  
  • if so then ₄₂Mo -> ₄₄Ru

Question 117

What is nuclear fission? What is spontaneous fission? How do lifetimes of spontaneous fission compare with alpha decay? How can the fission barrier be overcame?

Answer 117

• neutron hits a uranium nucleus -> nucleus spitting => two daughter nuclei + fast neutrons
• spontaneous fission is due to tunneling through the fission barrier
• overcome fission barrier in nuclear reactions by supplying an activation energy e.g. through neutron capture

Question 118

What are the products of fission? Why does fission process liberate several neutrons?

Answer 118

• mass distribution fission fragments from fission of 235-U is quite symmetric
• several neutrons are liberated because
  
  • heavy nuclei have large neutron excess (N>Z)
  • lighter fission fragments have less neutron excess => neutrons are liberated during fission (prompt evaporation neutrons)

Question 119

What is fission dynamics?

Answer 119

• governed by fission barrier height, nuclear viscosity and shell effects

Question 120

Which elements are primordial and which are stellar?

Answer 120

• primordial: H, He, Li, B, Be
• stellar: O, Fe, Th

Question 121

When was the Era of Nuclei to Particle Era and Era of Galaxies after the Big Bang?

Answer 121

• Era of Nuclei 10² sec
• 10⁰ sec to 10^-4 sec to 10^-6 sec
  
  • Nucleosynthesis of Helium
  • Nucleosynthesis Era
    
    • disappearanceof positrons, antiprotons, antineutrons
• Particle Era 10^-10 sec
  
  • confinement of quarks
  • formation of protons, neutrons, antiprotons, antineutrons
• Era of Galaxies => Galaxy and Star Formation
  
  • 1 billion - 5 billion years

Question 122

What is the Hubble constant?

Answer 122

• H(WMAP) = 71 ± 4
• H(PLANCK) = 67 ± 1.2

Question 123

What equations describe the adiabatic expansion of the universe and space?

Answer 123

• which implies S/V ∝ T³
  
  • S constant => 1/R³ ∝ T³=> T ∝ 1/R

Question 124

What is the Great Calibration? Temp (energy) vs. time

Answer 124

• Time
  
  • Hubble relation
    
    • v = Hd
  • eqn of motion
    
    • H = v/d = 1/R dR/dt
• Temp. (energy)
  
  • assume density of universe = density of radaition
  • Stefan-Boltzmann’s law ς_rad = σT⁴ [do I need the other eqns?]

Question 125

What is eqm black body radiation (BBR)?

Answer 125

• microwave background (λ = 7.35 cm) => T = 2.7 K
  
  • n_γ = 4*10⁸ photons/m³
  • ς_γ = 2.5*10⁵ ev/m³ (is this ev or eV?)
• from luminous matter
  
  • n_baryon ≈ 0.4 baryons/m³
• n_baryon/n_γ = η ≈ 10^-9

Question 126

How to go from Quark Gluon Plasma to Hadron Gas (confinement of quarks leading to the world of today)

3 quarks = baryon

quark + antiquark = meson

Answer 126

• annihilation of quarks and antiquarks => photons
• confinement of net quarks => hadrons
• confinement in detail => Hadrons grouped together => nuclei
• T = 175 MeV => t ≈ 10^-6 sec
  
  • after this time p and n are the only hadrons
    
    • mesons have decayed e.g. t_1/2(π) = 10^-8 sec

Question 127

What is the starting condition for nucleus formation? What is the ratio of neutrons and protons in eqm and at ‘freeze-out’?

Answer 127

• weak interactions: mix n and p, but stops after 1 sec => fix the n to p ratio
• neutrinos decouple at t ≈ 1 sec i.e. density of neutrinos is so small that neutrino capture no longer plays a role => ratio of n and p is fixed
• in eqm, ratio of neutrons and protons given by Boltzmann factor
  
  • at ‘freeze-out’, neutron to proton ratio is about (t = 0.01 sec after Big Bang)
    
    • N_n/N_p = 0.88 for kT = 10 MeV
    • => starting condition for nucleus formation

Question 128

What is primordial nucleosynthesis?

Answer 128

• neutron + proton => deuteron
  
  • D + D => 3-He
• first nuclei form: D, 3-He, 4-He, ..

Question 129

How is the deuteron formed? How to calculate fraction of photons with Eγ > E₀?

Answer 129

• n + p <-> D + γ (2.225 MeV)
  
  • deuterium only survives if number of gamma rays with Eγ > 2.225 MeV is sufficiently small
• integrate tail of black body radiation
  
  • N(Eγ > E₀) = integral of n(E) dE from E₀ to ∞
• plotting fraction f of photons of energies above E₀ gives T and time of formation of deuteron

Question 130

When were deuterons formed after the Big Bang? What is the critical factor for deuteron formation?

Answer 130

• formed between 3 mins and 15 mins after
  
  • limited by neutron decay time at 15 mins

Question 131

Why is primoridal nucleosynthesis quickly over?

Answer 131

• formation of Li and Be limited by Coulomb barrier (MeV)
  
  • temp now < 0.1 MeV (10² to 10⁵ s after)
• all other nuclei have higher binding energy than deuterium
  
  • hence more stable
• nuclei up to 7-Li and 7-Be can be formed
  
  • but reactions cannot go beyond A=7
  • because ⁸Be = > ⁴He + ⁴He (t_1/2 = 10^-16 sec)

Question 132

What does the present He abundance depend on?

Answer 132

• original n to p ratio
  
  • hence number of neutrino (lepton) families
• all neutrons end up in ⁴He => limiting factor
• N_He/N_p = 0.081 (calculated from N_n/N_p & corrected for β decay from t = 3-220 s)
• M_He/M_p ≈ 0.24
  
  • measurements predict that there are 3 families of leptons
  • more lepton families => mix n and p better => higher n/p ratio
    
    • hence more He
  • (is there a 4th family of neutrinos - sterile neutrinos?)

Question 133

When do atoms form and light decouples? Why? When do stars , galaxies and Our solar system begin to form? What are the different things dark matter is thought to be?

Answer 133

• when energy of light can longer ionise H (E < 13.6 eV)
  
  • light decouples (photons seen in CMB are from this period)
  • at this point, the Universe is about 1 million years old
• stars birth rate peaks at ~0.5 - 1 billion years
• early galaxy formation at t = 3 billion years
• Solar System forms at ~10 billion years
• 23% dark matter = WIMPs? Neutralinos? Axions? => LHC?
  
  • 73% dark energy

Question 134

What evidence is there for the expansion (a’>0) and reacceleration (a”>0) of the universe?

Answer 134

• general relativity predicts
  
  • (a”/a’) α - (ρ + 3ρ)
• => something out there with p < - ρ/3
  
  • => dark energy; what is it?

Question 135

What is stellar nucleosynthesis? What is the initial condition for it? How can heavier nuclei be made? How to improve barrier penetration?

Answer 135

• p+p -> α in stars (alpha capture for A < 60)
• fusion (tunneling model) is sub-barrier
  
  • height of Coulomb barrier limits fusion to lighter elements in smaller stars (low internal temp.)
• initial conditions from primordial nucleosynthesis M_He/M_p ≈ 0.24
• make heavier nuclei by
  
  • ⁴He + ⁴He -> ⁸Be -> ⁴He + ⁴He:
    
    • t(breakup) ≈ 10-16 s; Q = 91.9 keV
• Q = 7.45 MeV for ⁴He + ⁸Be -> ¹²C
  
  • => requires very large rate
• only possible through resonant reactions
• barrier penetration strongly enhanced if final nucleus has state that matches the incoming energy

Question 136

At which energy should we study astrophysical reactions on Earth?

Answer 136

• for a + X -> Y
  
  • reaction rate: R ∝ n(E) σ(E)
    
    • n(E) ∝ e-^E/kT√E
    • σ(E) ∝ (1/√E) e^-2G
    • => R ∝ e^-(E/kT)-2G
• curves for reaction ¹²C + ¹²C at temp. corresponding to kT = 0.1 MeV
• should be studied near the peak of the effective cross section

Question 137

Why do resonant reactions enhance the cross section? How wond the reaction rate change?

Answer 137

• due to overlap with final states of compound nucleus
• reaction rate: R ∝ n(E) σ(E)
  • n(E) ∝ e^-E/kT√E

σ(E) ∝ (1/√E) e^-2G -> σ(E) ∝ (1/√E) e^-2G S(E)

=> R ∝ e^-(E/kT)-2G

Question 138

When does alpha capture end?

Answer 138

• up to ⁵⁶Fe
• in heavy stars when He is used up
  
  • ¹²C + ¹²C -> ²⁰Ne + ⁴He
• relative abundance of C, O, Ne, Fe higher than the rest
• end at ⁵⁶Ni, ⁵⁶Co, ⁵⁶Fe (max. of binding energy curve)

Question 139

What is neutron capture? What is the cross section for formation determined by? What is the difference between the slow (S) process and rapid (R) process?

Answer 139

• stellar nucleosynthesis for A > 60
• build up of heavier elements by neutron capture (no Coulomb barrier)
• cross section for formation is determined by
  
  • neutron flux
  • element lifetime vs. Beta decay
• slow (S) process
  
  • all neutron flux, requires long half-lives
• rapid (R) process
  
  • large neutron flux wins over short half-lives

Question 140

What is neutron capture rate? What is it for a red giant star?

Answer 140

• red giant star: T = (1-2)*10⁸ K; nⁿ = 10¹⁴ m^-3
• rate corresponds to one capture per approx. 20 years
• => nuclear reactions proceed via the slow process
  
  • i.e. determined by beta half-lives of elements produced in the chain

Question 141

What do the neutron capture paths for r and s processes look like?

Answer 141

• blue = slow
• rapid = red
• green = superheavies (SHE)?

Question 142

How can heavier elements be produced?

Answer 142

• large neutron flux generated in supernova explosions
• heavy elements on Earth are thought to be due to mass accretion from debris from a local (in our Galaxy) supernova explosion

Question 143

How can exotic nuclei/beams be created?

Answer 143

• knowledge of ‘exotic nuclei’ i.e. unstable nuclei occuring in S and R processes necessary for astro calculations
• these nuclei cannot be made using stable projectiles and target nuclei
  
  • have to use unstable isotopes as projectiles
  • called Radioactive Isotope Beams or Rare Isotope Beams

Question 144

What is the uncertainty principle?

Answer 144

• Δp small => one wavelength
• Δp medium => wave packet made of several waves
• Δp large => wave packet made of lots of waves

Question 145

What is special relativity based on? What are the eqns for energy and momentum? What is not conserved?

Answer 145

• Einstein’s theory of special relativity brings space and time at the same level
• based on 2 postulates
  
  • speed of light is the same for all observers, no matter what their relative speeds are
  • laws of physics are the same in any inertial frame of reference (Lorentz invariant)
• m₀ = rest mas of a particle
• number of particles not conserved e.g. in a p-p collision, many particles are produced

Question 146

What is the energy and momentum at a given term in a relativistic collision e.g. A + B -> C + D + E?

Answer 146

Question 147

What is the Klein-Gordan eqn (free particle)?

Answer 147

• describes time evolution of ψ
  
  • works for spin 0 particles
• operators (observables) follow special relativity
• respects Lorentz invariance
  
  • space & time derivatives to the same power

Question 148

What is energy and momentum obtained from Klein-Gordan eqn using a simple plane wave ψ=e^{i(<strong>k.r</strong>-Et)}?

Answer 148

• ρ may take on -ve values
• -ve prob. density = probably not conserved?
  
  • considering Klein-Gordon eqn is second order in ∇

Question 149

What are the Pauli spin matrices?

Answer 149

Question 150

What is the Dirac eqn? What are its properties?

Answer 150

• γ depends on Pauli spin matrices
• Lorentz invariant
• includes spin (all fermions have spin)
  
  • no problem with -ve prob. density anymore
• ψ is not a complex number anymore, is a 4-component spinor

BUT

• still problem of energy solns < 0
  
  • solved by antiparticles
• still problem of conserved number of particles

Question 151

What is Feynman-Stuckelberg interpretation?

Answer 151

• interpret a -ve energy soln as a -ve energy particle which propagates backwards in time
  
  • or +ve energy anti-particle which progates forwards in time

Question 152

How does the quantum field theory (QFT) differ from (SR+QM)?

Answer 152

• fields for matter and for forces
  
  • continuous quantities over space
  • not wave fns
• particles are excited states of an underlying physical field
  
  • excited states have arbitrarily large number of particles
  • providing QFT systems with effectively an infinite number of degrees of freedom
    
    • particles are called field quanta
• Lagrangian formalism L = T-V; [L] = energy

Question 153

What is a vacuum in QFT?

Answer 153

• normally, vacuum is defined as state with no particles (classical)
• in quantum field, balls and springs are never stationary
  
  • always moving even when not enough energy has been added to the field to create a particle
• “virtual particles” can briefly and spontaneously appear from vacuum and disappear again even if insufficient energy
  
  • vacuum itself has random and indelible fluctuations
  • sometimes their influence can be felt by the way they kick around real particles

Question 154

How can a particle be created in the elementary field in QFT?

Answer 154

• light disturbances of the field does not work
• field only accepts energies above a certain threshold
• if the field is tapped hard enough
  
  • a particle is created
  • particle can propagate stably through the field

Question 155

What is the formula for a field in QFT??

Answer 155

• when (self or not) interacting fields are introduced, the number of particles is not necessarily conserved

Question 156

What is the principle of least action?

Answer 156

• can be used to derive the dynamics of any physical system
• when applied to a quantum system with Lagrangian expressed in terms of space-time fields, principle can determine the dynamics of elementary particles in QFT

Question 157

How are QM interactions between particles described in QFT? How does QFT approach the scattering when one e- emits a photon then recoils, then the photon travels to other e- which also recoils?

Answer 157

• interaction terms between corresponding underlying fields
• free field theory neglects interaction with other particles (fields)
  
  • unrealistic because even for one free particle, it interacts with the field it generates itself
• in QFT approach, a vibration in the e- field induces a vibration in the photon field
  
  • photon field vibration transports energy and momentum to another e- vibration and is absorbed
• this idea of fields and vibrations explains how the universe works at a deep and fundamental level
  
  • fields span all space

Question 158

What is meant by symmetry? What is meant by continuous symmetry?

Answer 158

• symmetry; any transformations of the generalised coordintates q, of the associated velocities dq/dt (possibly of the time variable t
  
  • that leaves value of the Lagrangian unaffected
• continous symmetry; symmetry with a continuous constant parameter, typically infiniteimal that can be dialled and that measures how far from the identity the transformation is bringing us
  
  • measures the size of the transformation

Question 159

What is Noether theorem?

Answer 159

• e.g. Lagrangian for a free particle: L = T-V = q²/2m
• examples of L invariant under infinitesimal translation
  
  • in space => total momentum conserved
  • in time => total energy is conserved
  • rotation => total angular momentum conserved

Question 160

Why does classical mechanics fail but special relativity works? What is another consequence of taking the Lagrangian to be Lorentz invariant?

Answer 160

• classical transformations treat time and space differently
  
  • CM fails because it is not Lorentz invariant
• special relativity treats time as a dimension (same footing as spatial dimension) and not just as a parameter
• conservation of 4 vector total momentum

Question 161

What are the three discrete symmetries associated with reversing direction of some quantity?

Answer 161

• charge conjugation
  
  • changing particles into anti-particles
• parity inversion
  
  • reversing direction of each of the 3 spatial coordinates
• time reversal
  
  • changing the direction of time

not obvious whether laws of nature should look the same for any of these changes

Question 162

What does parity change sign of? And what does it leave unchanged?

Answer 162

Changes sign of

• helicity
• posn
• velocity, momentum
• accn, force
• E field

Leaves unchanged

• time
• spin
• mass
• energy
• B field, magnetisation

Question 163

What are the intrinsic parity of elementary particle and antiparticles? What are the general formula for parity of mesons, baryons and photon?

Answer 163

• P(particle) = +1
• P(antiparticle) = -1
• P(meson) = P(q).P(anti q).(-1)^L = (-1)^L+1
  
  • comes from P property of spherical harmonics
• P(baryons) = P(q)(-1)^L1+L2+L3? = (-1)^L1+L2+L3
• P(photons) = -1

Question 164

What is meant by P number is conserved in all EM and strong interactions? What evidence is there for P violation in weak interactions?

Answer 164

• that reactions governed by EM and strong interactions are invariant under P transform
  
  • parity conserved if Hamiltonian is invariant under parity operation (reversal of sign of all the coordinates; true for strong and EM but not weak)
  • binding of quarks into hadrons is dominated by strong with influence from EM and a vanishingly small effect from weak
    
    • hence parity is another QN useful in defining a particle
• these 2 particles have same mass and lifetime, initially thought to be distinct ones since P was supposed to be conserved in all interactions
  
  • θ+ -> π+π0 => P = (-1)² =+1
  • τ+ -> π+π0π0 and π+π-π+ => P = (-1)³ = -1
• but Yang and Lee (1956) suggested that it is the same particle that can decay in states of different parity => hence P not conserved in weak
• Wu experiment
  
  • are A and B equally probable (can I count as many e- up as down (given direction for spin - direction of H; I don’t know what this means)?
  • No; neutrinos are mainly left handed and antineutrinos are right handed
  • parity not conversed in weak interactions

Question 165

What are the partiy of scalar (s), pseudoscalar (p), vector (polar vector) (v), pseudovector (axial vector) (a)?

Bold indicates a vector in space-time (4 components)

Answer 165

• P(s) = s
  
  • e.g. Higgs boson
• P(p) = -p
• P(v) = -v
• P(a) = -a

Question 166

What are the eigenvalues C operator can acquire? Which quantum numbers does it change the sign of and which does it leave unchanged? When is C number conserved?

Answer 166

• C(particle) = antiparticle => C²(particle) = particle
  
  • C² = 1 => C = ±1
  • some neutral particles can satisfy C(particle)= antiparticle = particle
    
    • e.g. π0 (C=1), γ (C=-1) not neutron, neutrino
• Changes sign of:
  
  • electric charge, magnetic moment
  • baryon number
  • strangeness
  • charm
  • beauty
  • top
  • other internal quantum numbers
• Leaves unchanged
  
  • spin
  • mass
  • energy
  • momentum
• conserved in strong and EM, not weak

Question 167

What evidence is there for C and P violation in weak interactions?

Answer 167

• decay of polarised muons (anti-muons)
  
  • observe angular distributions of e-s or e+s from decay in rest frame of decaying particle
• if decay is
  
  • C-parity invariant => expect Γ+ = Γ- and ξ+ = ξ-
  • P-parity invariant => expect ξ± = 0
• measured Γ+ = Γ- and ξ+ = -ξ-
  
  • hence both C and P are violated in muon decay

Question 168

Is CP a good quantum number to look at?

Answer 168

• No since in kaon, charm and beauty mesons systems CP is violated in weak interactions at level of 10^-3
• CP is good symmetry only for EM and strong interactions

Question 169

What does time reversal change?

Answer 169

• momentum and spin direction

Question 170

What is the CPT theorem? What principle arises from CPT invariance? Is CPT violated in weak interactions as well?

Answer 170

• CPT must be conserved in all interactions
  
  • e.g. particles and antiparticles have same mass and lifetime (CPT invariance theorem)
  • proving wrong by experiment => Nobel Prize
• principle of detailed balance
  
  • A + B -> C + D
  • C + D -> A + B (time T reverseal)
    
    • happen at the same rate
• would expect T to be violated in weak since CP is but CPT is not (though it is hard to measure)

Question 171

What is P and T violation of the neutron due to? What is D of the electric dipole moment (EDM) in qD expected to be?

Answer 171

• P and T violation due to EDM of the neutron
• expect D to be 10^-15
  
  • since neutron has radius of about 10^-13
  • include charge and other effects
• experiment shows neutron EDM < 0.29*10^-25 e-cm

Question 172

What is crossing symmetry?

Answer 172

• occur at about the same rate
  
  • only exception is if kinematically not allowed (energy not conserved etc.)
• trivial, the theoretical calculations (probability to happen) are the same (e.g. revert arrows in Feynman diagrams and respect conservation of lepton, baryon etc.)
  
  • e.g. anti-v p -> n e+ OK then
    
    • v n -> p e- OK
    • anti-v n -> p e- DOES NOT EXIST

Question 173

What are the baryon and lepton numbers for each quark, anti-quark, lepton, anti-lepton? What about for hardons, baryons, antibaryons and mesons? Why are baryon and lepton numbers only assumed to be approximately conserved? What is the only evidence for single lepton flavour number violation?

Answer 173

• hadrons, B is defined to be
  
  • B = 1/3 [N(q) - N(anti-q)]
• baryons have B = 1
• antibaryons have B = -1
• mesons have B = 0
• there is no operator (transformation) that implies the existence of conserved quantities lepton and baryon number
  
  • but no evidence is yet seen for total baryon or lepton number violation
  • e.g. in a process A + B + C … -> F + G + H …
  • total L and total B are conserved, and in all interactions that have been tested
• only exception is in the neutrino sector (since neutrinos are seen to oscillate)

Question 174

What are neutrino oscillations? Where is this observed?

Answer 174

• (b)
• happens in the atmosphere when neutrinos propagate down to Earth and while this occurs, v_μ -> v_e
  
  • only observed case of single lepton flavour number hanging

Question 175

What suggested the hypothesis that a baryon number must be conserved in EM interactions? (Before lepton number conservation was hypothesised) What phenomenon can you think of that implies B number violation?

Answer 175

• p -> e+ γ (does not happen)
• matter-antimatter asymmetry & neutron oscillations

Question 176

What is isospin?

Answer 176

• p and n are 2 states of the same particle (nucleon); differ by isospin
• pion is the strong interaction particle
• flavour symmetry in strong interactions = hadrons in patterns can be obtained by rotating in flavour space (all different flavour states of the same particle)
  
  • => isospin is conserved in strong interactions
• strong interaction between us and ds is the same
  
  • consider total angular momentum of bond state (including spin) and small quark mass differences
    
    • can explain masses and magnetic moments of hadrons quite well
• isospin symmetry is not an exact symmetry of strong interactions (p and n are not identical except for their charge; what? they don’t have the same charge) but a good approximate one

Question 177

What is Gellmann-Nishima formula?

Answer 177

• Y = B + S hypercharge
• I₃ = Q - Y/2 isospin
  
  • Q = electric charge
• see if one can organise and find pattern => Eightfold way
  
  • why these patterns => quantum chromodynamics (QFT)

Question 178

What are other numbers that are conserved in EM or strong interactions apart from lepton and baryon numbers?

Answer 178

• strangeness (S) = - [N(s) - N(anti-s)]
• charmness (C) = N(c) - N(anti-c)
• beauty (B) = - [N(b) - N(anti-b)]
• top (T) = N(t) - N(anti-t)
• upness (U) = N(u) - N(anti-u)
• downness (D) = - [N(d) - N(anti-d)]

Question 179

What is perturbation theory? What are the assumptions under which this and Feynmann’s diagrams for interaction between particles hold?

Answer 179

• systematic method for expanding in the coupling constant
• when Lagrangian is the sum of free particle and interaction terms
  
  • each interaction has a multiplicative factor ig (or iα) = coupling constant
  • expand interaction-field theory around free-field theory as a power series in ig
  • interaction conceived as a small perturbation on free theory => interaction can be calculated as a Taylor expansion in ig

Question 180

What is the probability amplitude M of a diagram with N vertices?

Answer 180

• α^N/2
• or M² of order α^N

Question 181

What does each vertex equal in QED?

Answer 181

• ig_eγ_μ
  
  • γ_μ is same matrix seen in Dirac’s eqn
  • g_e = √α_EM

Question 182

How can you test for QED experimentally?

Answer 182

• can measure α(Q) in ee -> μμ scattering
  
  • α(Q) increases with Q (i.e. closer to bare charge; large R test charge sees screened e- charge)

Question 183

What is the “Dirac” magnetic moment for the tree-level Feynman diagram on the left? What about for higher order diagrams?

Answer 183

• expressed in terms of g-factor μ = gSe/2m
  
  • where S = spin & g = 2 from first order diagram
• a = anomalous magnetic moment = (g-2)/2 is predicte dto be different from 0 due to higher order diagrams

Question 184

How is the weak interaction unique?

Answer 184

• only interaction changing flavour of quarks (i.e. changing one type of quark into another)
  
  • sees 3 families of falvour whereas photon interacts individually interacts with each charged particle
• propagated by carrier particles (W, Z) that have significant masses, feature explained in Standard Model by Higgs mechanism
• only interaction that violates P and CP symmetry (recall experimental evidence lecture 2, p11 and 15)

Question 185

What is helicity?

Answer 185

• projection of spin along direction of flight of a particle
• not Lorentz invariant (can always find a reference system where LH looks RH) => only L. inv. if mass = 0
• helicity is commuting with H => a set of eigenstates for helicity is also a set of eigenstates for H
• Dirac soln in base u1, u2 (v1, v2 for anti-particle) => Diract soln in base u↑, u↓ (v↑, v↓)

Question 186

Which part of the L and R (chiral) components of left-handed helicity particle and anti-particle spinor part-take in weak interaction with W exchange?

Answer 186

• L part

Question 187

What is lepton universality principle?

Answer 187

• interactions of e- and its associated neutrino should be identical to those of muon and its neutrino, or tau and its neutrino => meaning strength is the same or α_weak at W lepton neutrino vertex is identical

Question 188

Is W interaction with lepton doublet really identical to interaction with quark doublet (lepton-quark symmetry of weak interactions)?

Question 189

How was the charm quark existence first considered?

Answer 189

• Cabibbo mixing matrix couldn’t explain why the measured decay rate of us du was much smaller

Question 190

Which particles participate in charged current weak interactions in ultra-relativistic limit E>>m?

Answer 190

• only left-handed particles and right-handed antiparticles
• helicity of
  
  • left-handed particles = -1
  • right-handed particles = +1

Question 191

What is QM unitarity violation?

Answer 191

• when QM calculation gives larger flu of W bosons than incoming flux of e-s/e+s

Question 192

What is the electroweak unification relation?

Answer 192

Question 193

What are the predictions of electroweak theory?

Answer 193

• electroweak symmetry
  
  • if we know sinθ_W from ratio of strength of W and Z interactions at low energy (G_Z/G_F) => predict Mw and Mz
• Higgs particle
• something to do with cross section and differential cross section

Question 194

What are tests of the electroweak theory?

Answer 194

• LEP collider

Question 195

What is Forward-Backward Asymmetry? What is it a result of?

Answer 195

• AFB = σ_F - σ_B/σ_F + σ_B
• result of the fact Z couples to LH and RH chiral fermions differently

Question 196

How many free parameters are there in the Standard Model?

Answer 196

• 18 (but 19 apparently)
  
  • 9 fermion masses
  • 3 CKM mixing angles + 1 phase
  • 1 EM coupling constant
  • 1 strong coupling constant
  • 1 weak coupling constant
    
    • G_F = 1.16637*10^-5 GeV^-2
  • 1 Z⁰ mass
    
    • m_Z = 91.187621 GeV/c²
  • 1 Higgs mass

Question 197

What is gauge symmetry, global and local symmetry transformation? What is the ‘gauge principle’?

Answer 197

• global symmetry transformation; when sphere is simply rotated about its axis, shapes of lines are not changed
  
  • local symmetry transformation; lines of longitude and lattitude are twisted
    
    • shape of ballon does not change; remains invariant or is conserved in these transformations
• Gauge principle is the requirement that U(1) phase invariance should be local
  
  • generated interaction between Dirac fermion and gauge field A; nothing else than the vertex of GED

Question 198

What is spontaneous symmetry breaking?

Answer 198

• way to keep Lagrangian gauge symmetric (all particles apparently massless), and yet add mass terms for fermions and bosons
• requires adding a new complex field - Higgs field (spin 0, I3W = 1/2)