MM3 Flashcards
1
Q
What is the general Fourier series for period 2L and what are the formulas for coefficients?
A
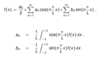
2
Q
What is Parseval’s identity for Fourier expansion between -π and +π?
A
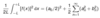
3
Q
What is meant by a regular singular point?
A
- p0 and q0 are both finite at x0
- what’s x0
4
Q
How to find the inverse of matrix A?
A
- A-1 = CT/|A|
- CT is the cofactor of A
- like finding determinant AND with the +-+- stuff
5
Q
What is the Fourier transform f(k) of a function f(x)?
A
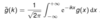
6
Q
What is the Parseval’s identity for Fourier transform?
A
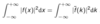
7
Q
How to determine polynomial solutions?
A
- Find when series terminates
- expand the series soln up to the point where the series terminates
8
Q
How to use dummy variables?
A
- Sub the power needed e.g. j in the original series e.g. j-1, replace variable in original series with j’ so j’-1 = j
- set j’=0 (or whatever the start point of the original series was) to get the new start point of the series e.g. j=-1
9
Q
What is the flux through a surface (assume closed)?
A
- n vector for any closed surface always points outwards
- e.g. magnetic flux

10
Q
How to determine if the field F through a point is a source or a sink?
A
- depends on div of F
- ∇.F > 0 => source
- ∇.F < 0 => sink
11
Q
What is the divergence theorem?
A
- outward flux of a vector field of a closed surface = volume integral of the divergence over the region inside the surface
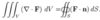
12
Q
How to evaluate line integral?
A
- see if F is parallel or perp. to dr
- (dr = dr er)
- if perp. then F.dr = 0
- if parallel then F.dr = F dr
- can predict line integral using Stoke’s theorem
- so for a conservative field, the integral of a closed loop is 0
13
Q
What is Stokes theorem?
A
- line integral of a loop enclosing surface Σ = surface integral of the curl of the field
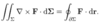
14
Q
A


