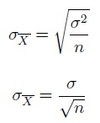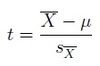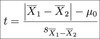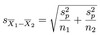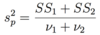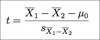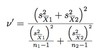Stats Flashcards
What are the two kinds of statistics in respect to their use?
1) Descriptive statistics: Measures of central tendency and variability
2) Inferential statistics: Parameter estimation, defining uncertainty, determining reasons for variation.
Bias
Any systematic deviation between sample estimates and a true value
Inference
Drawing a conclusion from a premise.
Premise
A premise is a statement we assume is true (e.g. data and observations).
The two kinds of variability in a study
1) Variability related to the variables we’re investigating.
2) Variability that is not interesting in the context of what we are investigating (noise variability).
What is the purpose of inferential statistics?
1) To discriminate between interesting variation and noise variation.
2) To determine the probability of observing such variability if a scientific mechanism was not operating.
What is an informal way think of “statistically significant” as?
Statistically significant = unlikely to hve ocurred by chance.
How does statistical analysis fit into the scientific method?
Statistical analysis allows for an objctive assessment of evidence in support or against a hypothesis.
What is a scientific hypothesis?
A scientific hypothesis is a proposed cause and effect relationship between a process and an observation.
Observation = what Hypothesis = how
What is a statiscial hypothesis?
Simply a statment about whether there is or not a pattern of interest in the data.
What are the two types of statistical hypotheses?
- H0* (null hypothesis) = No effect on predictor variable
- HA* (alternative hypothesis) = Effect on predictor variable
What are the two kinds of variables in an experiment?
1) Predictor variable (aka independent variable)
2) Response variable (aka dependent variable)
What is µ0 “mew not” in a one-sample study?
µ0 is the true population mean.
What is α?
α is a set proability criterion we use to reject a null hypothesis. It’s a set chance for incorreclty rejecting a null hypothesis.
In testing a hypothesis, what is a sample used for?
In testing a hypothesis, we use a sample to estimate characteristics of an underlying population.
The statement “We calculate the proability H0 is true, given the data” is wrong.
1) Why is this?
2) What is the correct statment?
1) Population paremeters are fixed, so either H0 is true or not.
2) The correct statment would be “We calculate the probability of oberving the data we gathered given a H0”.
How are the N0 and NA formualted in a one-sample test?
- H0*: µ = µ0
- HA*: µ ≠ µ0
OR
- H0*: µ - µ0 = 0
- HA*: µ - µ0 ≠ 0
To test a hypothesis we use a test statistic. Broadly, how is a test statistic calculated?
Test statistic = effect (i.e. µ - µ0) / error
How is a test statistic used for testing a hypothesis?
1) Either comparing the test statistic to a critical value
or
2) calculating a p-value associated with that test statistic
How is a p-value interpreted?
The p-value can e though of as the probability of observing the data if the H0 was true.
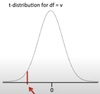
In the example of a z statistic, what is z?
z is the number of stander deviations by which the observed mean differs from the population mean.
What does the central limit theorem state?
The CLT states that the distribution of means from a non-normal populaion will not be normal but will approximate normalityas n increases.
How is population variance calculated?
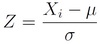
How is sample variance calculated?
What is standard error and how is it calculated?
The standar error (aka SE, SEM) is the standard deviation of a statistic (in this case mean) and is calculated as:
Noting that we don’t know σ,
How is SE estimated?
Up to 19:00
We can estimate SE as:
This is because the best estimate for population variance σ is sample variance s.
What is the relationship between sample size n and variance in the distribution of sample means?
The variance in the distribution of means will decrease as n increases.
How si the t statistic calculated
1) What is the distribution shape difference between z-distribution and t-distribution?
2) What effect does this have on a critical value?
1) In the t-distribution, there is more area at the distribution tails. Also the t-dsitribution is “pushed at the top”.
2) a t-critical value is more extreme than a z-critical value (see bars in the figure)
Note: Remember than for a normal distribution, the percentage of values in an area can be known with the number of standard deviations form the mean.
★ one sample t-test example
We want to know whether drug A significantly changes the body temperature of healthy human adults 2 hours after taking the drug. Note that the normal body temperature is 37 °C. We take our measurements from a sample and find a mean temperature of 38.5 °C and a variance of 3.4. The sampe size is 30.
Note: On the final exam we’ll have to calculate variance, which will not be given to us.
s = sqrt(3.4/30) = 0.3366502
t = (38.5 - 37)/0.3366502 = 4.456
Then we look up the t critical value in a table using:
two tailed, 29 df, and an α of 5%,
and get a value of 2.045.
Because 4.456 > 2.045 we reject the null hypothesis and cunclude that drug A significantly changes body temperature.
When do we use a t statistic instead of a z statistic?
We can’t use z if we are estimating σ from s.
What is the value of v (derees of freedom) for an hypothesis about mean?
v = n - 1
How does the location of the critical value of a one-taled test differ from the critical calue of a two-tailed test?
For a one-tailed test, we put the entire rejection region into one tail of the t-distribution, instead of splitting it between the two tails.
In the following t-distribution graph, you wold reject the null hypothesis if the t-value was less than the critical value (shown in red).
What is t thought of as?
Like z, t is the number of standard deviations from the mean.
What are the typed of errors in hypothesis testing?
1) Type I error (α) = rejecting true H0
2) Type II eror (β) = failing to reject a false H0
Note that: When µ ≠ µ0, the critical value defines the boundary between power and type II error.
In a t-distribution, why do we need to know the degrees of freedom?
The degrees of freedom are needed because the distribution shape changes for different degrees of freedom.
Note that t-tables only tell us whether the p-value is greater or less than a specified α.
If instead of using tables, you want to know the p-value, how do you calculate it?
In R, you can use:
1 - pt(4.456,29)
In an example similar to the drug A and temperature example, when would you use a one-sampled test?
You would use a one-tail test if you’re only interested in whether body temeprature is either increasing or decreasing as a result fo the drug.
In an the drug A and temperature example, how would you write the one-tailed statistical hypotheses in the following cases?
1) We want to know whether the drug increases body temperature
2) We want to know whethr the drug decreases body temperature
1) We want to know whether the drug increases body temperature
- H0*: µ - µ0 ≤ 0
- HA*: µ - µ0 > 0
2) We want to know whethr the drug decreases body temperature
- H0*: µ - µ0 ≥ 0
- HA*: µ - µ0
Note that the = sign always is part of H0 and not *HA
H0*
: µ - µ0 ≤ 0
HA: µ - µ0 > 0
What is the formula for a two-sample t-test looking for any diffeence between the two samples?
What is the formula for a two-sample t-test with a given µ0 different than 0 (i.e. looking for a specific difference between two sample means)?
In a one-sample t-test we use s to estimate σ.
In a two-sample t-test we do something similar. We assume that s1 and s2 are similar, but not the same, so we use s2p as a pooled variance estimator (see formula).
How is s2p calculated?
where SS is sum of squares.
How is the formula for two-sample one-tailed t-test different from the two-tailed formula?
In the formula for one-tailed t-tests, the values of the means are not absolute.
Using the visual representation of a t-distribution, explain why we always need to accept some level of error.
We need to accept some level of error because the t-distribution asymptotes at the x axis and there is no value of t that corresponds to a proability of 0%.
What is statistical power?
Statistical power (1 - β) is the probability of correclty rejecting a false H0
What is the relationship between power and the difference between µ and µ0?
The greater the difference between µ and µ0, the greater the power we have to deect the difference.
What does the probability of a type II error depend on?
The probability of a type II error depends on:
1) what HA is
2) how large an effect we hope to detect
3) sample size
4) how good the experimental design was
When we set an α of 0.05, we often have a β of around 0.2 and a power of around 0.8.
★ Welsch’s test example
We want to test for a difference in protein concentration between two pea populations. We determine variances are heterogenous and thus use a Welsch’s test:
Results:
meanfert = 24 g protein
SSfert = 261 g2
nfert = 30
meanunfert = 21.8 g protein
SSunfert = 320 g2
nunfert = 29
- *s2f** = SSf / (nf - 1) = 261/29 = 9
- *s2u** = SSf / (n<span>u</span> - 1) = 320/28 = 11.43
t’ = (x̄1 - x̄2)/sqrt(s21/n1 + s22/n2)
= (24 - 21.8)/sqrt(9/30 + 11.43/29) = 2.6406
Wilsch has a different distribution, so we need to use a special formula to calculate the degrees of freedom:
v’ = (s2x̄1 + s2x̄2)2/(s2x̄1)2/(n1 - 1) + (s2x̄2)2/(n2 - 1)
but first:
- *s2x̄f** = s2f/nf = 9/30 = 0.3
- *s2x̄u** = s2u/n<span>u</span> = 11.43/29 = 0.3941
- *v’** = (s2x̄1 + s2x̄2)2/[(s2x̄1)2/(n1 - 1) + (s2x̄2)2/(n2 - 1)] =
(0. 3 + 0.3941)2/(0.3)2/29 + (0.3941)2/28 = 55.6939
Now that we know v’ we check the t-table and find t0.05(1),55.6939 = 1.672677 ⇒ N0 rejected
What increases statistical power?
These elements increase statistical power:
1) greater difference between µ and µ0
2) larger α
3) larger n
4) smaller σ2
5) one-tailed tests
For a one-tailed Mann-Whitney / Wilcoxon test, you have to decide which is the tail of interest. How does this work?
What are the assumptions of one-sample t-tests?
1) Data are a random sample
2) Each data point is independent from each other
3) Data come from a normally-distributed population
Note: One-sample-t tests are robust against non-normality as long as data are symmetrical.
How are the statistical hypotheses written for testing the proability of getting different means from two populations?
H0: µ1 = µ2
HA: µ1 ≠ µ2
OR
H0: µ1 - µ2 = 0
HA: µ1 - µ2 ≠ 0
What are the assumptions for a two-sample t-test?
1) data are random and independent
2) Both samples come from normally-distributed populations
3) Both populations have equal variances
★ two-sample two-tailed t-test example
We want to test for a difference in protein concentration between two pea populations:
Results:
meanfert = 24 g protein
SSfert = 261 g2
nfert = 30
mean<sub>unfert</sub> = 21.8 g protein SS<sub>unfert</sub> = 320 g<sup>2</sup> n<sub>unfert</sub> = 29
- H0*: µ1 - µ2 = 0
- HA*: µ1 - µ2 ≠ 0
s2p = (SSf + SSu)/dff +dfu = (261 + 320)/(29 + 28) = 10.193 g2
sx̄f-x̄u = sqrt(s2P/nf + s2p/nu) =
sqrt(10.193/30+ 10.193/29) = 0.8314 g
t = (x̄f - x̄u)/s<em>x̄f - x̄u</em> = (24 - 21.8)/0.8314 = 2.645
v = 57, t-critical = 2.0.
absolute value > critical value, so we reject the null hypothesis.
For the following one-tailed test hypotheses, based on the relationship between the observed and critical t-values, when do you reject the null hypothesis?
1) HA: µ1 - µ2 < 0
2) HA: µ1 - µ2 > 0
1) HA: µ1 - µ2 < 0
* H0* is rejected if t ≤ tα(1),v’
2) HA: µ1 - µ2 > 0
* H0* is rejected if t ≥ tα(1),v’
Note that for a two-tailed test,
For a two-tailed test,
HA: µ1 - µ2 ≠ 0
we reject H0 if | t | ≥ t ≥ tα(2),v’
★ two-sample one-tailed t-test example
We want to test the hypothesis that bean protein concentration increases by at least 2 g/100 g beans when bean plants are fertilized. We do the study and get the following results:
meanfert = 24 g protein
SSfert = 261 g2
nfert = 30
dffert = 29
meanunfert = 21.8 g protein
SSunfert = 320 g2
nunfert = 29
dfunfert = 28
- H0*: µ<span>f</span> - µ<span>u</span>**HA: µ<span>f</span> - µ<span>u</span> ≥ 2
- s2p* = (SSf + SSu)/dff +dfu = (261 + 320)/(29 + 28) = 10.193 g2
sx̄f-x̄u = sqrt(s2P/nf + s2p/nu) =
sqrt(10.193/30 + 10.193/29) = 0.8314 g
t = (x̄f - x̄u)/sx̄f-x̄u = (24 - 21.8 - 2)/0.8314 = 0.240558
v = 57, t-critical = 1.67.
Because out t-value is less than the t-critical, we cannot reject out null hypothesis that there is a difference of at least 2 g between both treatments.
What assumption violations is the t-test most sensitive to?
T-test is quite robust to considerably non-normality, but violation of random/independence and homogeneity of variances is serious.
- For the figure below, in which two-sample t-test would there be higher power?
a) A
b) B
a) A
* *b) B**
- Use the figure below to answer the next 3 questions. Which area under the curve(s) represents the probability of correctly not rejecting the null hypothesis?
A) A
B) B
C) C
D) D
E) A + D
F) C + B
A) A
B) B
C) C
D) D
E) A + D
F) C + B
- In the figure above, which area under the curve(s) represents the probability of incorrectly not rejecting the null hypothesis?
A) A
B) B
C) C
D) D
E) A + D
A) A
B) B
C) C
D) D
E) A + D
- In the figure above, if this hypothesis test were performed at a significance level of 0.01, what probability would A represent?
A) 0.05
B) 0.975
C) 0.01
D) 0.0005
E) 0.005
A) 0.05
B) 0.975
C) 0.01
D) 0.0005
E) 0.005
Which two factors increase rubustness against heterogenous variances in a t-test?
T-tests are a little bit more robust against variance heterogeneity if:
1) sample sizes are similar
2) sample sizes are above 30
2) the test is two-tailed
How are assumptions of a two-sample t-test tested?
1) data are random and independent: cannot be checked. Done from experimental design.
2) Both samples come from normally-distributed populations: Visual inspection and Shapiro-wilk test
3) Both populations have equal variances:
Visual inspection and Fligner - Killeen test
One example of violation of the independence assumption is when samples are paired (repeated measues). How could you get around the assumption of independence with paired data?
Paired data can be combined into a new sample by calulating their differences and this will now make data points independent.
For two-sample analysis, how do you analyse the data in the following scenarios?
1) Both samples normal and equal variances
2) Both samples normal but unequal variances
3) Both samples non-normal but equal variances
4) Both sampes non-normal and unequal variances
1) Both samples normal and equal variances:
two-sample t-test with pooled variance
2) Both samples normal but unequal variances:
Welsch’s two-sample t-test (no pooled variance)
3) Both samples non-normal but equal variances:
Mann-Whitney or Wilcoxon rank test
4) Both sampes non-normal and unequal variances:
Transformation and re-assessment
Note that for Welsch’s test, we use a t’ statistics instead of a t statistic.
Same as v’, which is a different calculation of df.
What is the main characteristics of the Mann-Whitney / Wilcoxon test?
It’s a non-parametric test. Because of this:
1) It does not require estimation of population paameters
2) Hypotheses are not statements about population parameters
However,
3) it assumes that the data are random
How are data treated in a Mann-Whitney / Wilcox test?
What is a drawback of this test?
Data are ranked wither from high to low or from low to high.
Convertion of data into ranks causes a loss of information and therefore power.
For the following samples of germination times, fill in the “Rank A” and “Rank B” columns with the ranks that we would assign to these data in order to do a two-sample Mann-Whitney/Wilcoxon test.
Step 1: assign ranks to all numbers. If a number is repeated, they still get ranks n+1 where n is the previous rank.
Step 2: average the ranks in the repeated numbers.
What are the two statistics calculated in a Mann-Whitney / Wilcoxon test?
How are they calculated?
u = n1n2 +[n1(n1 + 1)]/2 - R1
u’ = n1n2 - u
★Mann-Whitney / Wilcoxon test example
Height of males: 193, 188, 185, 183, 180, 175, 170
Height of females: 178, 173, 168, 156, 163
Ranks of male heighs: 1, 2, 3, 4, 5, 7, 9.
Ranks of female heighs: 6, 8 ,10, 11, 12
n<sub>m</sub> = 7 n<sub>f</sub> = 5 R<sub>m</sub> = 31 R<sub>f</sub> = 47
R is the sum of the ranks from each sample
- H0* = Male and female students are the dame height
- HA* = Male and female students are not the same height
Not that no hypothesis is made on any population parameters.
u = n1n2 + n1(n1 + 1)/2 - R1
= (7)(5) + (7)(8)/2 - 31
= 35 + 28 - 31
= 32
u’ = n1n2 - u = (7)(5) - 32 = 3
Then you compare either u or u’, whichever is larger to the u critical (uα(2),n1,n2). If greater, reject H0.
This calculaton is not done by hand for in the exam.
★Mann-Whitney / Wilcoxon test in R
How do you do this in R?
1) make a string will all the data:
height
2) make a string corresponding to sex for each data point
sex
3) test:
wilcox.test(height~sex)
- What is a t-value?
a) A variance
b) A number of standard errors from the mean for a t-distribution with a given number of degrees of freedom
c) A statistic that, without any other information, tells you whether your alternative hypothesis is true
d) A non-parametric test statistic
a) A variance
b) A number of standard errors from the mean for a t-distribution with a given number of degrees of freedom
c) A statistic that, without any other information, tells you whether your alternative hypothesis is true
d) A non-parametric test statistic
- On a standard normal distribution, 95% of the observations are contained within how many σ of μ? Choose the best approximation.
a) 1
b) 1.645
c) 2
d) 2.5
e) 3
a) 1
b) 1.645
c) 2
d) 2.5
e) 3
- In which of the following situations should we select a Welch’s two-sample t-test as the most appropriate and powerful option for conducting a hypothesis test?
a) Both samples are non-normally distributed, sample variances are equal, and sample distributions are similar
b) One sample is non-normally distributed and variances are unequal
c) One sample is non-normally distributed and variances are not equal
d) Both samples are normally distributed, and variances are equal
e) Both samples are normally distributed and variances are unequal
a) Both samples are non-normally distributed, sample variances are equal, and sample distributions are similar
b) One sample is non-normally distributed and variances are unequal
c) One sample is non-normally distributed and variances are not equal
d) Both samples are normally distributed, and variances are equal
e) Both samples are normally distributed and variances are unequal
- Which statement about the following study description is correct?
A herbicide-resistant strain of wheat and a non-herbicide resistant strain of wheat are grown, with 30 plants of each in a greenhouse before they are sprayed with a new herbicide that is going on the market. The researcher wants to test whether the herbicide-resistant strain (which was genetically engineered for resistance to different herbicides than the one being tested in this study) shows better growth and seed set than the control, following the spray.
a) The dependent variables are growth and seed set.
b) In a graph of the seed set results, seed set should be plotted on the x-axis.
c) A one-sample test is appropriate for this situation.
d) A paired-sample test is appropriate for this situation.
a) The dependent variables are growth and seed set.
b) In a graph of the seed set results, seed set should be plotted on the x-axis.
c) A one-sample test is appropriate for this situation.
d) A paired-sample test is appropriate for this situation
- Which of the following statements is correct?
a) A statistical hypothesis is a statement about a cause-and-effect relationship between 2 or more variables.
b) A scientific hypothesis is a statement about a cause-and-effect relationship between 2 or more variables.
c) A statistical hypothesis must be proved to accept or reject a scientific hypothesis
d) “Descriptive statistics” refers to testing how much variation in an observed variable is due to a predictor variable, versus how much is due to chance alone.
a) A statistical hypothesis is a statement about a cause-and-effect relationship between 2 or more variables.
b) A scientific hypothesis is a statement about a cause-and-effect relationship between 2 or more variables.
c) A statistical hypothesis must be proved to accept or reject a scientific hypothesis
d) “Descriptive statistics” refers to testing how much variation in an observed variable is due to a predictor variable, versus how much is due to chance alone.
- If we are interested in testing a hypothesis about a difference in two means, as the uncertainty (error) of our estimates of the means increases, our chance of detecting a real difference:
a) Decreases
b) Increases
c) Is not affected
- *a) Decreases**
b) Increases
c) Is not affected
- Conceptually, why is the standard error of the mean always smaller than the standard deviation of a sample, when both are derived from the same sample data?
a) Standard deviation is a measure of sample variability, whereas standard error of the mean is an estimate of the standard deviation of the distribution of sample means from which that sample is assumed to have come, and distributions of sample means are always narrower than the sample distribution from which they are estimated.
b) Standard deviation is not always smaller than the estimate of standard error derived from the same sample. It is bigger when sample size is large (>30).
c) Because the standard deviation represents the 95% confidence interval, whereas standard error represents one standard deviation of the distribution of sample means.
d) Standard deviation is the width of the distribution of sampling means, whereas standard error is a measure of sample variability, and the distribution of sample means is always more variable than a single sample.
a) Standard deviation is a measure of sample variability, whereas standard error of the mean is an estimate of the standard deviation of the distribution of sample means from which that sample is assumed to have come, and distributions of sample means are always narrower than the sample distribution from which they are estimated.
b) Standard deviation is not always smaller than the estimate of standard error derived from the same sample. It is bigger when sample size is large (>30).
c) Because the standard deviation represents the 95% confidence interval, whereas standard error represents one standard deviation of the distribution of sample means.
d) Standard deviation is the width of the distribution of sampling means, whereas standard error is a measure of sample variability, and the distribution of sample means is always more variable than a single sample.
- What is the Central Limit Theorem?
States the following:
The distribution of means taken from a population which is or not normal will approximate normality as sample size increases.
- What is a p-value?
The probability of collecting certain data if H0 was true.
- For a two-tailed t-test, with α of 0.05, what does the lower critical value tell us?
It tells us the t-value below which there is a 2.5% or lower chance of having gotten a sample t-value that small if the null hypothesis was true.
The probability of rejecting a true H0 is called Type ______ Error.
Type I error
The probability of failing to reject a false H0 is called Type _____ Error.
Type II error
The Greek symbol for the proability of rejecting a true H0 is
alpha
The Greek symbol for the probability of failing to reject a false H0 is
betta
Power =
Power = 1 - betta
List the 3 assumptions of a two-sample t-test.
1) data is random and independent
2) both samples are normally-distributed
3) both samples have equal variances
note: there is no simple mathematical relationship beteen type I and type II error
How are statistical hypotheses for a paired samples test written?
H0: µd = µ0
HA: µd ≠ µ0
where µd is the mean difference between pairs
A test-statistic for two samples can be expressed as:
How does this scale up to mulptiple samples?
Why does a test with multiple samples have to use two tails?
one-tail tests do not make sense when we have more than two samples.
We conduct a study in which we raise a cohort of 36 goldfish in one large tank for one year. We then place 12 of the goldfish in a small pond, 12 in a medium-sized pond, and 12 in a large pond. We leave them in these ponds for 1 year, and then collect them all and measure their lengths.
What are we trying to determine using a test-staistic?
We use a test-statistic to see if the differences in the means that we found are statistically significant (i.e. if we would observe similar differences if the experiment was repeated.
Based on the following image, how do we measure effect?
To measure effect we measure the distance of each group mean from the overall mean of all samples.
Differences (X̄i - X̄),
where i is the group identifier and X̄ is the overall mean:
X̄1 = - 1. 69
X̄2 = 0.22
X̄3 = 1.47
Research hypothesis: adult goldfish grow larger when they live in larger ponds.
How do you write this as a statistical hypotesis if we have 3 samples?
- H0*: Mean fish size is the same in all pond sizes
- HA*: Mean fish size is not the same in all pond sizes
An often seen but incorrect way to write this:
- H0*: μL = μM = μS
- HA*: μL ≠ μM ≠ μS (not correct)
Note that SSamong is the numerator of the t-statistic.
test-statistic = ssamong/error
Now we need the error for the denominator.
Based on the following image, what is n, N, and k?
- n* = number of observatons (j = 1 to ni) within each group, ni
- N* = total number of observations
- K* = number of groups (in this case ponds)
- n1* = 12; n2 = 12; n3 = 12
- N* = 36
- k* = 3
Based on the following image, what are the two kinds of error we can think about?
1) deviation of each observation from its group mean (SSwithin)
2) deviation of each observation from the overall mean (SStotal)
1) Xi - X̄i
2) Xi - X̄,
where Xi is each observation, X̄i is group mean, and X̄ is overall mean
The formula for SSwithin is:
What is the formula for SStotal?
The formula for SStotal is:
Note that SStotal equals the sum of SSamong and SSwithin
SStotal = SSamong + SSwithin
Differences (X̄i - X̄),
X̄1 = - 1. 69
X̄2 = 0.22
X̄3 = 1.47
How do we avoid differences cancelling out?
to avoid differences calcelling each other pout, we use squares AND multiply by sample size to weigh;
Squared differences ni(X̄i - X̄)2
X̄1 = 34.45
X̄2 = 0.59
X̄3 = 26.01
Then, summign that, we get:
SSamong groups = ∑ni(X̄i - X̄)2 = 61.06
What is error in statistics?
Error is any deviation of an observation from the true mean of its population.
How is the F-ratio aka F-statistic composed?
The F-statistic is composed of:
variance due to deviation of group means from overall mean (Effect), divided by variance due to deviation of each observation from its group mean (Error)
Note we’re dividing variances.
The F-statistic has a known distribution.
What does the shape of the F-distribution depend on?
The shape of the F-distribution depends on the DF of the numerator and the DF of the denominator.
What are the degrees fo freedom for
SStotal, SSamong, SSwithin?
SS<sub>total</sub> = *N* -1 SS<sub>among</sub> = *k* - 1 SS<sub>within</sub> = *N* - *k*
Note that also DFtotal = DFamong + DFwithin
Results from ANOVA are reported in ANOVA tables.
How would an ANOVA table look the previous example?
SSAmong groups = 61.06
DFAmong = 2
MSAmong = 30.53
SSWithin groups = 119.5
DFWithin = 33
MSWithin = 3.62
F = 8.43
Instead of using SS, we use MS, which makes SS into variance terms.
How do you calculate MS?
MSamong = SSamong/DFamong
We saw the following visual representation of the fish ANOVA data:
What is another way of plotting?
Another way of plotting is response variable on y-axis and predictor variable on x-axis.
How do you calculate MSerror?
What are other names for MSerror?
MSerror = SSwithin/DFwithin
= SSerror/DFerror
MSerror is also called MSwithin interchangeably.
MSerror also called residual.
Why do we use DF as a denominator instead of sample size?
DF represents the number of observations available to estimate a parameter.
What statistic do we use for a test with multiple samples?
F-statistic aka F-ratio
Why is F-statistic also known as F-ratio?
The F-statistic is a ratio between two variances.
Just like for the normal distribution, we can calculate the area under the curve for a given point or critical value.
What is the formula for F-critical?
Fcrit = Fα(1)DFamong,DF2within
What is a very important assumption of an F-statistic?
F assumes that the variances come from normally-distributed populations.
For the fish size and lake size example:
SSAmong groups = 61.06
DFAmong = 2
MSAmong = 30.53
SSWithin groups = 119.5
DFWithin = 33
MSWithin = 3.62
F = MSamong/MSwithin
F = 30.53/3.62 = 8.43 F<sub>0.01(1),2,33</sub> = 3.28 - (for some reason we used α of 0.01)
We reject the null hypothesis and conclude fish size is not equal across ponds.
In a case where k = 2:
1) we could use either an F-test or a T-test and get the same result
2) MSerror = s2p
3) F-value will equal the t-value squared
Fα(1)1,(N-2) = (tα(2),(N-2))2
4) If a one-tailed test is required, the t-test is applicable, but ANOVA is not.
Note that we use one tail in the notation of the F-value formula. This is because the F-distribution is assymetrical and has only one tail.
Why do we need to do multiple comparisons?
To know which means are signifficantly different from one another.
Why is it invalid to use multiple t-tests after an ANOVA?
Multiple t-tests inflate type I error.
plotting the results of a Tukey test in R:
plot(TukeyHSD(model))
gives us 95% confidence intervals
Results from Tukey tests are often plotted:
Tukey test results also plotted with lines
What test do you use if sample sizes are not equal?
How is it different from Tukey?
Tukey-Kramer test
Different from regulat Tukey beacuse it uses a different SE term:
What happens if you want to do a Tukey or Tukey-Kramer test but the variances across samples are unequal?
Tukey is sensitive to different variances, so you can use the Welsch approximation for the Tukey test:
If we wanted to test:
H0: μ1=μ2 AND H0: μ2=μ3 AND H0: μ1=μ3
What is the proability of incorrectly rejecting at least one of the three H0’s?
What is the problem with this?
the probability of incorrectly rejecting at least one of the H0’s is:
1− (1 − α)C = 1 − (1 − 0.05)3 = 0.14,
where C is the number of possible different pairwise combinations of k samples
The problem is that 0.14 is much larger than 0.05
What do multiple comparison procedures control for?
Multiple comparisons control for the experimentwise type I error by keeping it at α.
What is the meaning of α when doing multiple comparisons?
for multiple comparisons, α is the probability of commiting at least one type I error
What are the two options for peforming multiple comparisons?
1) posthoc comparisons
2) a priori (pre-planned) contrasts
1) Specifically, what are posthoc comparisons used for?
2) Specifically, what are pre-planned constrasts used for?
1) posthoc comparisons are used to compare all pairs of means
2) pre-planned constrasts are used to rest a limited subset of hypotheses
Tukey test aka honestly significantly different test (HSD) or wholly significant different (WSD).
★ How is the MS of a contrast calculated?
float numbers are means of treatments
14 is n in every treatment
Can Tukey test be used without doing an ANOVA?
Yes, Tukey tests can be performed without first doing an ANOVA.
Note that not all posthoc tests can.
What is a disadvantage of doing a Tukey test after an ANOVA, instead of doing the Tukey test first?
Doing an ANOVA test before a Tukey test can lower statistical power.
Nonetheless, the common practice is to do the ANOVA and hen Tukey.
What are the steps for doing a Tukey test?
Assuming that the two sample sizes are equal:
1) Arrange and number all sample means in order of increasing magnitude
2) Calculate pairwise differences between the means X̄i – X̄A
(Note i is the group with the highest mean)
3) Calculate q-statistic: divide a difference between two means:
q = (X̄B - X̄A)/SE
where SE = sqrt(s2/n)
Note that you calculate a q for each comparison
4) H0: X̄B = X̄A is rejected if q is greater than q-critical, qα,df,k
The conclusions of the Tukey test depend on the order in which the pairs of means are compared.
What is the proper procedure for comparing pairs of means?
1) Largest mean compared against smallest mean, then against second smallest, so on…
2) Second largest mean compared against smallest, then second smallest, so on…
How is it demonstrated that the SS of contrasts is partitioned among the 3 orthogonal contrasts?
The SSamong equals the SS of the 3 contrasts added together:
What can we conclude if there is no significant differnce between 2 means is found?
if no significant differnce between 2 means is found we can conclude that there are no significant differences between eclosed means
Calculate of q-statistics for the fish experiment example:
Mean 1 = 3.917
Mean 2 = 5.833
Mean 3 = 7.983
SE = 0.549
q-crit = q0.05,33,3 = 3.407
q-crit = q0.05,33,3 = 3.407
- 3 vs 1:** (7.083 - 3.917)/0.549 = 3.166/0.549 = 5.767 ⇒ reject *H0
- *3 vs 2:** (7.083 - 5.833)/0.549 = 1.25/0.549 = 2.277 ⇒ H0 not rejected
- 2 vs 1:** (5.833 - 3.917)/0.549 = 1.916/0.549 = 3.49 ⇒ reject *H0
What is a disadvantage of using a priori tests instead of post hoc?
a priori tests do not allow comparisons of all pairs of means
What is something a priori contrasts allow to do but post hoc don’t?
- a priori* contrasts allow to compare one mean against an average of other means
- a priori* constrasts are also more powerful than post-hoc
Researchers are interesrted in determining whether there are positive effects of two common sponge species on the root growth of a mangrove tree.
Treatments:
A: unmanipulated
B: fake spongo
C: sponge species 1
D: sponge species 2
the ANOVA yielded a p-value of 0.003
1) what does orthogonality mean?
1) orthogonality means that the contrasts are independent from one another
example of orthogonal contrasts:
If living sponge tissue enhances mangrove root growth, then the average growth of the two living sponge treatments should be greater than the growth of roots in the inert foam treatment
How are the coefficients of these contrasts computed?
control (0)
fake sponge (2)
sponge spp 1 (-1)
sponge spp 2 (-1)
what are the degrees of freedom of a contrast?
1 df
★ how is the F-ratio of a priori contrasts calculated?
MS/MSerror =
0.145/0.164 = 0.882
The formula for SSwithin is:
why is orthogonality important?
ortogonality ensures that P-values are not inflated
what are the rules for orthogonality?
1) sums of coefficients must equal 0
2) for k treatment groups, only k - 1 contrasts
3) the sum of cross-wise coefficients must also be 0
In this example, are contrasts orthogonal?
Why?
contrast one:
control (0)
fake sponge (2)
sponge 1 (-1)
sponge 2 (-1)
contrast two:
control (3)
fake sponge (-1)
sponge 1 (-1)
sponge 2 (-1)
They are orthognal because:
1) their coefficient sums are 0 in both cases
2) their number is lower than k - 1
3) their cross-products equal 0:
(0) (3)+(2)(-1)+(-1)(-1)+(-1)(-1) = 0
what are the components of ANOVA table?
1) source of variation
2) degrees fo freedom
3) sums of squares
4) mean squares
5) F
6) p- value
What is a required conditionto use a priori contrasts?
they have to be determined before doing the statistical analysis
what does sample non-normality suggest?
sample non-normalit suggests population non-normality
What happens if the ANOVA assumptions are not met and an ANOVA is performed anyway?
the result of the ANOVA cannot be trusted if the assumptions are not met
why are assumptions important for ANOVA?
what are the assumptons of ANOVA?
ANOVA is a parametric test
assumptions:
1) independent, random samples
2) all samples come from normal populations
3) variances between all treatments are equal
What test is performed instead of ANOVA if sample variances are unequal but distributions are normal?
Welch’s ANOVA for unequal variances
what test is performed instead of ANOVA if sample variances are equal but distributions are non-normal?
Kruskal-Wallis
what is done if samples for an ANOVA are neither normal nor have equal variances?
transformation an assumption re-assessment
how is the assumption of variance homogeneity checked?
1) Visual assessment (histograms or QQ-plots)
2) Fligner-Killeen test
When can QQ-plots not be used?
QQ-plots are not adviced for samples with fewer than 25 observations. In that case, histograms are better
how is the asumption of normality checked?
normality is checked through
1) assessment (hisrograms)
2) Shapito-Wilk test
How does Kruskal-Wallis ranked test work?
1) assign ranks to observations
2) tied observations get average of the ranks they would get if not tied
What is a disadvantage of the Kruskal-Wallis ranked test?
observations lose information when they are converted to ranks
what is P-hacking?
trying different analyses until one is significant
Statistically, why is P-hacking wrong?
P-hacking changes the actual α value
Other ways fo P-hacking:
- taking too many data points
- not adjusting p-values for multiple comparisons
What does alpha represent in a Tukey test?
In a Tukey test, alpha represents the probabiltiy of commiting at least one Type I error among all comparisons
Note that:
when k=2, either an ANOVA or a t-test can be used, and the F value will equal the t vaue squared
However:
If a one-tailed test is required, then an ANOVA cannot be used
how are data treated in linear regression?
pairs of data. x-values paired with y-values
in a real life situation (where variation is present), what is the equation for linear regression?
Ŷi = α + βXi + εi
how are data from linear regression plotted?
data from linear regression are plotted in a scatterplot.
what is the equation for linear regression assuming a perfect model?
Ŷi = α + βXi
in
Ŷi = α + βXi
1) what is α?
2) what is β?
1) α is the intercept (i.e. of Ŷi where the line crosses y axis
2) β is the slope of the line (i.e. the increase in Ŷi every unit of X)
α and β are population parameters
How are they estimated?
we stimate α and β from our sample as a and b
in Ŷi = α + βXi + εi,
what is ε
ε is error (i.e. the departure of an Yi from a Ŷi).
where Ŷi is what the equation predicts Yi to be
What is the sum of all εi?
the sum of all εi equals 0
what method is used to calculate the linear regression parameter estimates?
Least Squares
what does Xi Yi mean?
Xi Yi is a singple point (pair of X and Y)
what is Xi,Ŷi?
Xi,Ŷ is a point corresponding to an X that falls on the line of best fit
what is the difference between Xi,Yi and Xi,Ŷi called?
the difference between Xi,Yi and Xi,Ŷi is called a residual
what is the equation to calculate the slope?
What is the equation to calculate the intercept?
we derive from the first equation to calculate α
What happens if you change the inercept but not the slope?
Line moves up or down
note that a negative intercept makes the line cross X blow Y = 0
what happens if you change the slope?
The line moves, but anchored at the intercept
what does the Least Squares method calculate?
the Least Squares metod calcualtes the equation for the line that minimized differences between Y an Ŷ
visually estimating the slope
Slope = (Y2 – Y1)/(X2 – X1) Slope = (10 − 16) / (5 − 2) Slope = (−6) / (3) Slope = −2
why should extrapolation not be done in regression?
The function does not hold infinitely, not awat from the intercept and not into the intercept either
calculating α and β from two points
1) calculate β
2) use Ŷi = α + βXi
b = (20 – 0) / (3 – 1) = 10
Use the point (3,20) to calculate a:
a = Y – bX =
20 – 10*3 = -10
Interpolation in linear regression is not wrong
what population parameter are we interested in from linear regression?
we’re interested in β because that’s the parameter that defines the relationship between predictor and response variable
1) determine variability of the response variable, SSY or SStotal
2) determine the amount of variability among Yi, “regression of sums of squares” or SSR or SSreg
Note: the last formulae are easiest for hand calculations
To obtain SSR we need:
What is the difference between simple linear regression and simple linear correlation?
simple linear regression assumes dependence of oen variable upon another
in simple linear correlation there’s a relationship but not dependence
What is residual error in a regression and how is it obtained?
residual error as a measure of the scatter of data points around the regression line.
Using SSR, SSY, and SSresid, we have partitioned the total variation in Yi into variation explained by the regression line and variation not explained by the regression line
SSY = SSR + SSE
AKA
SStotal = SSregression + SSresidual
Note: the lines don’t add up because they are not yet squared
What does β tell us?
β tells how much the response variable Y increases per unit increase of predictor variable X
what are the assumptions for linear regression?
1) for each value of X, Y must be random an independent of one another
2) for each X, there exists a normal distribution of Y (and a normal distribution of ε
3) homogeneity of variances in the population (the variances of the distributions of Y values must all be equal)
4) relationship between X an Y is linear (mean of Yi lies in a straight line)
5) measurments of X are obtained without error (impossible, so we assume error is irrelevant)
We use b, but what we;re really interested in is β
What is β?
β is the functional dependence in the population
what are the hypotheses for linear regression?
H0: β = 0
HA: β ≠ 0
How is the value of r2 interpreted?
r2 = 1 means all the variation in Y is explained by X
r2 = 0 means all the variation in Y is explained by X
How can hypotheses about β be tested?
ANOVA or t-test method
Note: testing anything other than H0: β =0 (e.g. H0: β - β0) requries that we use a t-test
Regression using t-test for hypothesis about a:
SSR will be equal to SSY only if each data point falls on the regression line (very unlikely).
How are the DF calcualted in regression?
DF<sub>reg</sub> = 1 DF<sub>total</sub> = n - 1 DF<sub>resid</sub> = n - 2
with the DF you can now calculate the MS’s
MS<sub>reg</sub> = SS<sub>reg</sub>/DF<sub>reg </sub> MS<sub>resid</sub> = SS<sub>resid</sub>/DF<sub>resid</sub> F = MS<sub>reg</sub> / MS<sub>resid</sub>
What is r2, aka coefficient of determination?
r2 indicates how strong the relationship is
aka
how much of the total variation in Y is attributed to X
How is r2 calculated?
r2 = SSreg/SStotal = SSR/SSY
Regression using t-test for hypothesis about b:
t = (b - β0) / Sb
where Sb is
Sb = sqrt(s2XY * SSX)
OR
Sb = sqrt(MSresid/SSX)
and
MSresid = sum(Yi - Ȳi)2/(n -2)
Formulae for t-critical
tα(2),n-2
tα(1),n-2
What is the concept of a degree of freedom?
if you calculate the mean from a set of numbers n, one of thos numbers is not free to variable and df is n - 1
what isone definition of degrees of freedom?
the number of values in the final calculation of a statistic that are free to vary int he daata sample
the maximum number of logicaly independent values
What are the two types of degrees of freedom?
DF associated with the effect of interest
DF associated with the error
1) What are DF in ANOVA?
2) What are DF in regression?
ANOVA: DFgroups = k - 1 (where k is the number of groups)
Regression: DFreg = 1
In linear regression, why does DFreg = 1?
In regression we only calculate 1 parameter more than the mean of Y (remember the mean of Y is a).
Ȳ = a + bx
what is the generalformula for error DF?
DFerror = n - p
Where n is sample size and p is the number of parameters used for estimations
For regression, DFerror = n-2 becaue we need to know a and b
