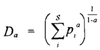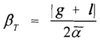Analysis of ecological communities Flashcards
Biodiversity data reduction
Summarization of how sample units relate to each other, Two types:
- Categorization.
- Creating synthetic variables (e.g., ordination).
Problem with using traditional multivariate tools in community ecology
Data are accompanied by unwanted properties
Questions asked by comunity ecology
What are the species living in an area and why?
What controls diversity?
Ordinal variables
Categorical variables of a ranked nature
Nominal variables
Categorical variables of a qualitative nature with no inherent rank
Dummy variables
Categorical variables with n possible states transformed into binary variables in which 1 or 0 represent presence or absence of something categorical.
Discontinuous variables
Variables with fixed numerical values (e.g., percent)
Continuous variables
Variables with potential infinite numerical values. In practice, seldom true (e.g., set graduations in a measuring device).
Routes for analyzing a species matrix
Q route: Relationships among sample units
R: Relationships among species
Transposing (matrices)
Flipping a matrix vertically or horizontally.
In a normal matrix species are treated as axes;
In a transposed matrix, species are treated as points.
Calculated matrices
Matrices wholes values are calculated from multiplying variables from an original matrix.
Metaobjects
A sample containing objects sich as species, environment, treatment, and species traits.
Columns and rows of a matrix are considered objects.
Each pair of objects can potentially form a different matrix, altough not always conceptually appealing.
Sparse matrix
A matrix containing many zero values.
Relativization
Standarizing a number of variables into a single scale (e.g., number of standard deviations from the mean).
Focal species
A species in a community with special interest (e.g., a rare species interesting for conservation).
Focal species-habitat relationship
Two ways to examine:
1. Species-centeres approach: predict species performance from habitat variables (e.g., regression)
- Habitat-centered approach: describe variation in habitat variables and evaluate species position within that variation (e.g., ordination).
Sampling (McCune’s definition)
The process of selecting objects of study from a larger number of those objects, where each object is subjected to one or more measurements.
Examples of species abundance measurements
- Cover
- Frequency
- Counts
- Biomass
- Basal area
- Importance values (average of >1 sampling measurements)
- Presence/absence
- Size-class data
Types of sampling schemes
- Random
- Stratified random
- Regular (sample units are spaced at regular intervals)
- Arbitrary without bias (haphazard)
- Subjective (e.g., we sampled the most diverse landscapes)
Sources of random numbers
Random number tables, stopwatch, etc.
Types of cover sampling units
- Fixed area: circles, squares, rectanlges
- Point intercept: percent cover is calculated as proportion of hits by points
- Line intercept: percent cover measured as proportion of a line superimposed on a species
- Distance method: Distance from a randomly chosen point to nearest tree (based on the concept that distances can be used to calculate the mean area occupied by an object).
Number of sample units (rule of thumb)
For every imporant controlling factor, 20 additional sample units are needed;
Alternatively, a species accumulation curve can be used to calculate needed number of samples (when a curve flattens out, addiitonal sampling stops being beneficial).
Measures of sample adequacy
Precision: Increases with addiitonal digits.
Accuracy: How close a measurement is from reality
Bias: Any systematic directional error
Measuring accuracy
A sample taken as “the truth” is taken by intensive sampling and resampling an area with dufferent observers and a large number of sampling units.
Sample size-number tradeoff
Many small samples: results in an incomplete species list
Few large samples: results in overestimating rarer species
Pseudoreplication
When replicates are not trully independent (e.g., spatially non-independent plots)
Repeated measures
Succesive measurements from one sample result in correlation (e.g., samplig an area on different dates).
Pseudo-turnover
Seemingly change in a community due to sampling biases (e.g., differet observers)
Nesting (aka multistage sampling)
Subsampling within a sample unit
Paired sampling
Samples pairs are identical except for the condition of interest.
Only really achievable under controlled conditions.
Topographic variables
- Aspect of a slope (direction that it faces; degrees need to be transformed)
- Heat load: Amount of solar energy a slope receives
- Slope correlation of distances (physical distances in a slope need to be transformed)
Diversity (formula)
where α is a constant assigned; S = number of species; Dα = diversity measure based on constant l Pi = proportion of individuals in a particlar species i
Diversity and uncertainty
Maximum diversity yields maximum diversity in the species that one will draw next from a sample.
Three applications of B-diversity in relation to environmental gradients
- Direct gradient: the environmental gradient is directly measured
- Indirect gradient: a gradient is presumed from measures of a species
- No specific gradient: compositional heterogeneity without reference to a gradient
Rate of change, R
Refers to the steepness of a species response in relation to a gradient. Can be graphed against the gradient (see image).
Gleasons
Unit of species change. Simiar to R, masures steepness of a species response curve.
It’s the sum of slopes of individual species at a point along the gradient axis.
Half-change
The amount of change in a community resulting in 50% similarity.
A gradient that is 3 half-changes long means that the community has changed by half three times.
Beta turnover
Measurment of species change in a commuity with presene/absence data. Uses gained species, lost species, and α.
Pielou’s J
Measure of species evenness calculated as:
J = H’/logS
, where H’ is the Shannon inex
Distance curve
Works by calculating the average distance between the centroid of a subsample and the centroid of a whole sample. The more representative the sample, the shorter the distance.
Distance curves have an inverse distribution to richness.
Problems in species response curves in response to gradients (in relation to real data)
- Zero truncation: Abbundance cannot be lower than 0
- Curves are solid: Species is usually less abundant than potential
- Curves are complex: Can be polymodal, asymmetric, discontinuous, etc.
Frequency distribution of species abundance (most common characteristic)
Usually resemble negative binomial distribution (strongly skewed).
Bivariate distributions
Used to examien the relationship between the distributions of two species.
A) positively associated
B) Negatively associated
Dust bunny distribution
Commonly observed in a scatterplot of one species versus another.
Most sample units lie along the corners of the p-dimensional space.
The more strongly correlated the variables, the more elongate the curve.
B in relation to species matrices
If β = 1, the matrix is full;
If β = 3, the mean sampling unt has 1/3 of all species.
Double zero problem
many common methods for examining relationships between species take absence as an indication of a positive relationship.
Therefore, as (0,0) values are added to a dataset, negative association move toward positivity.
This issue prodcues data misinterpretation.
The flexibility of using distance to analyze biological communities
- Resemblance can be measured as dissimilairty (distance) or similarity
- Distance measures can be converted into similarities and vice-versa
- Distance can be applied to binary and quantitative data
Graphical representation of the following dataset in ordination
* Alterntively, sample units as points along species axes
Three main categories of distance measures
Metric, semimetric, nonmetric
Metric distance measures
Obbey thre rules:
1) min values is 0 for two identical items
2) distance is possitive for two differing items
3) Ssymmetry: distance from A to B = distance B to A
3) Triangle inequality axiom: with three objects, the distance between two objects cannot be longer than the sum of the other two
Semimetric distance measures
Violate the triangle inequality axiom
Nonmetric distance measures
Violate one or more metric distance measure rules
Euclidean distance
A distance measure based on the Pythagorean theorem
Manhattan (city block) distance
Distace measure calculated while moving along one direction at a time
Correlation coefficient (r) (distance measure)
Distance measure calculated by using the angle beteen lines connecting two poins with a centroid;
It eliminates scale incompatiblities between values
(i.e., different orders of magnitude between values)
r = cos(angle)
Rescaling: rdistance = (1 - r)/2
Proportion coefficients
Distance method consisting of city bock distance expressed as proportions of the maximum distance possible;
Includes Sorensen coefficient (aka Bray-Curtis coefficient): 2w/(A+B) and
Jackard coefficient: w/(A+B-w),
Where w is the area overlapping between curves.
w can be represented by the overlap between two curves of species abundance against an environmental gradient.
Quantitative symmetric dissimilarity (QSK)
Throws different results with raw vs relativized data.
When data is relativized, gives the same result as Sorensen.
Relativized Sorensen
Distance measure that is equivalent to Bray-Curtis coefficient when data are relativized by sampling unit (SU) total.
Relative Euclidean distance (RED)
Distance measure designed to put differently-scaled variales on the same scale. Ranges from 0 to 1.
Chi-square distance
Distance measure that usually performs poorly, but can be sueful for some ordination techniques.
Mahalanobis distance (D2)
Corrects for correlation in original variables;
Can be used to test outliers by calculating distance between each point and remaining points in the cloud;
Functions similarly to an F ratio;
Distance: Loss of sensitivity (concept)
All distance measures show a degree of curvilinearity as the environmental gradient axis elongates, losing seinsitivity (this effects is strongest for correlation coefficient measure).
Redundancy
Where a pair of species fails to be informative, another pair of species will be.
Nonmetric multidimensional scaling (NMS) (advantage over other techniques)
It’s based on ranked distances. This allows to linearize the relationship between distance in species space and distance in an ordination space.
Criteria for choosing distacne measures
1) Availability in stastistical packages
2) Compatibility with a particular multivariate analysis
3) Theoretical basis (e.g., what the distance measure represents)
4) Intuitivity (ease of interpetability)
Geodesic distance method vs shortest path method
While aiming to use the shortest distance possible, the shortest path method considers only one point at a time, while the geodisic method considers all points at a time
For the following dataset, calculate Euclidean distance and Manhattan distance for sites AB
Euclidean distance AB = sqrt(1+1+1+1+81) = 9.165
Manhattan distance AB = 1+1+1+9 = 12
Outliers
Sample units with extreme values.
for individual variables (univariate outliers) or multiple variables (multivariate outliers).
Note multivariate outliers are not necessarily univariate outliers.
Ways of detecting multivariate outliers
1) Mahalanobis distance
2) Calculate number of standard deviations for distance
3) Look for isolated entities in clusters
Types of data transformations for multivariate analysis
1) Monotonic transformations
2) Beals smoothing
3) Relativization
4) Double relativization
Monotonic transformations (examples)
1) Power (xp): p = 0 gives presence absence; square root (p =0.5) and other roots.
2) Logarithmic: log(x). Requires special treatment for zeros (not recommended)
3) Arcsine: (2/π) * arcsin(x); requires proportion data
4) Arcsine squareroot (2/π) * arcsin(√x): Spreads the ends of the scale for proportion data
Beals smoothing
Designed for community data.
Replaces each cell in the community matrix with the proability of the target species occuring in that particular sample, based on the joint occurrences.
Replaces presence/absence data with quantitative values.
Relativization
Rescales individual rowsor column in relation to one criterion (e.g., maximum, mean, median, SD…)
Most effective when row totals are unequal.
(consistency of row totals can be evaluated by the coefficient of variation: CV = 100*(SD/mean))
Weighting by ubiquity
A type of relativization that gives more weight to species tat occur in many samples.
Information function of ubiquity
Based on information theory, maximum weigt is applied to species occurring in 50% of the samples because they provide the most information.
Double relativization
Relativizations applied serially in a given combination.
Deleting species
Deleting species based on very low occurrences is ok for studies interested in correlation. The aim in this is trying to reduce noise. Correlation coefficients peaks at an intermediate level of species retention.
Deleting species when the aim is to examine patterns of species diversity is not correct.
Combination of entities
In community matrices, sampling units can be combined (averaged) provided they are similar enough.
Difference between two dates
Before and after data on species abundance can be analyzed by difference instead of original values
bij = aij2 - aij1
Grouping strategies for multivariate analysis
1) Hierarchical (groups nested witin groups)
2) Nonhierarchical (groups not related to a particular level of grouping)
3) Polythetic: Use diferent species for decigin groupings/divisions
4) Monothetic: Grouping based on one species (or variable) of interest
5) Agglomerative: Groups formed by fusion
6) Divisive: Starts with a group of everything and sequentialy divides
Dendrogram grouping and information
Information is lost as groups are made.
The objective function measures informaton lsot at each step and allows rescaleing from 0 to 100% information. The goal is to maximize information and minimize grouping (groups should still be interpretable ecologically).
Multivariate regression trees
Hierarchical grouping method. Impurity of groups is the sum of the squared Euclidean distance from individual samples units to the centroid.
Nonhierarchical grouping
Groups are specified and then items are placed into those groups.
Evaluating quality of groups
Chaining is the addition of single items to existing groups. Chaining increaes path lenght, so the goal is to reduce chaining.
Circularity
testing for differences among groups using variables that were used to define groups.
