Simple Linear Regression

Question 1

σ² or V

Answer 1

the degree to which a variable ‘varies’ around its
mean

Question 2

∑(X-xbar)²/N-1 = ∑ SS/df

Answer 2

= σ² or V

Question 3

SD

Answer 3

√σ² or √V

Question 4

Covariance

Answer 4

CoV = the degree to which two variables ‘vary’ simultaneously
or co-vary

Question 5

Answer 5

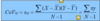
SXY = covariance of X and Y
∑xy = sum of the cross products. The deviations of pairs of X and Y scores from their means

This is not sqaured, it is now the variation of two variables together. It is divided by the degrees of freedom.

Note: the variance of a variable is… its covariance with itself.

Question 6

Correlation (rxy)

Answer 6

the degree of linear
relationship between two variables and, essentially, it is a
standardised covariance

Question 7

Answer 7

Just as with standardised and unstandardised regression coefficients, if we know the SDs (or variances) of the variables, we can easily convert from covariances (unstandardised rxy) to correlations (standardised rxy) and back.

Think of correlation as a covariance, where the variance of X and Y are standardised. Suppose we convert X and Y to z scores (M=0, SD=1) our formula for converting from a covariance to a correlation then becomes (2nd image) when the variables are standardised.

Question 8

What can MR do that ANOVA cannot?

Answer 8

1. MR can use both categorical and continous independent variables
2. MR can easily incorporate multiple IVs
3. MR is appropriate for the analysis of experiemental or nonexperiemental research