MR Chapter 3

Question 1

Why R²+ r²+r²

Answer 1

R² also depends on the correlation between the independent variables

Question 2

What is the formula for R²

Answer 2

Question 3

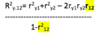
What happens when the IVs do not correlate?

Answer 3

1. If the IVs don’t overlap (don’t correlate), then R² will equal r²+r².
2. When the IVs correlste, ß’s are not equivalent to and are usually smaller than the original r’s. When the IVs are uncorrelated, the ß’s are again equal to the correlations, as in simple regression.

Question 4

Is R² less or more than r²+r²?

Answer 4

As a general rule, the R² will be less than the sum of the squared correlations of the IVs with the DV. (r²+r²). The only time R²= r²+r² is when the IVs are uncorrelated.

Question 5

How do you get to predicted scores in SPSS?

Answer 5

When you go ‘save’ -> tick Predicted values: Unstandadised, and then also tick Residuals: Unstandardised.

Question 6

How can we calculate the residuals?

Answer 6

The residuals are the left over part when we compare the actual minus the predicted grades.

Y = a + bX₁ = bX_{2­ ­­} + e

Y’ = a + BX_1­ + BX₂

Y-Y’ = e

Another way of thinking about it is residuals are the original DV (grades) with the effects of the IV (pared and HW) removed.

Question 8

What does optimally weighted mean?

Answer 8

It would not be accurate to just weight the IVS by half, or a logical amount. If you did this, the (explained variance) R² will not be as high and the unexplained variance, 1 – R² will be higher.

If the two IVs are optimally weighted, the line is best fitting to the data of all straight lines.

Question 9

Why is it called least sqaures regression?

Answer 9

The regression weights the IVs so as to minimise the squared residuals, thus least squares.

• If you add up all the residuals, they equal zero.
• Pos and neg cancel out. If you first square them, then add them up, the number is smaller than for any other possible straight line.

Also called OLS (ordinary least squares) regression

Question 10

What happens if you presume the weighting of variance?

Answer 10

If you logically said that HW explained 75% of the variance in grades, and pared explained 25%, the solution would actually explain slightly less of the variance than the least squares method.

Question 11

What happens if you have few residuals?

Answer 11

Because the F equation depends on the residuals, the regression is likely to be significant the smaller the residuals. It will be less biased data, and will more strongly represent the population.

Question 12

Regression Equation = creating a composite?

Is it possible to make a single IV that matches the predicted score?

Answer 12

Yes, instead of weighting HW and Pared by .75 and .25, we could have weighted them by ßs from multiple regression equation to create a composite.

MR provides an optimally weighted composite, a synthetic variable, of the IVs and regresses the DV on this single composite variable.